Ermitteln Sie rechnerisch einen Term der ersten Ableitungsfunktion \(f'\) von \(f\) und berechnen Sie die \(x\)-Koordinate von \(T\).
(5 BE)
Lösung zu Teilaufgabe 1d
\(f(x) = \dfrac{x^2-4}{x+3} = x-3 + \dfrac{5}{x+3}; \; D_f = \mathbb R \backslash \{-3\}\) (vgl. Teilaufgabe 1c)
Erste Ableitungsfunktion \(f'\)
Am einfachsten ist es, den Funktionsterm \(f(x) = \dfrac{x^2-4}{x+3}\) mithilfe der Quotientenregel abzuleiten.
\[f(x) = \frac{\textcolor{#0087c1}{x^2-4}}{\textcolor{#cc071e}{x+3}}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\begin{align*}f'(x) &= \frac{\textcolor{#0087c1}{2x} \cdot (\textcolor{#cc071e}{x+3}) - (\textcolor{#0087c1}{x^2-4}) \cdot \textcolor{#cc071e}{1}}{(\textcolor{#cc071e}{x+3})^2} \\[0.8em] &= \frac{2x^2 + 6x -x^2+4}{(x+3)^2} \\[0.8em] &= \frac{x^2+6x+4}{(x+3)^2} \end{align*}\]
Zum Vergleich ist nachfolgend die Ableitung des Funktionsterms \(f(x) = x-3 + \dfrac{5}{x+3}\) aufgeführt, einmal mithilfe der Quotientenregel und einmal nach Umformung in die Potenzschreibweise mithilfe der Kettenregel.
\[f(x) = x-3 + \frac{\textcolor{#0087c1}{5}}{\textcolor{#cc071e}{x+3}} = x-3 + 5 \cdot \textcolor{#0087c1}{(\textcolor{#cc071e}{x+3})^{-1}}\]
\[\begin{align*} f'(x) &= 1 + \frac{\textcolor{#0087c1}{0} \cdot (\textcolor{#cc071e}{x+3}) - \textcolor{#0087c1}{5} \cdot \textcolor{#cc071e}{1}}{(\textcolor{#cc071e}{x+3})^2} \\[0.8em] &= 1 - \frac{5}{(x+3)^2} &&| \; \text{gemeinsamer Hauptnenner:}\; (x+3)^2 \\[0.8em] &=\frac{(x+3)^2}{(x+3)^2} - \frac{5}{(x+3)^2} \\[0.8em] &= \frac{x^2+6x + 9 - 5}{(x+3)^2} \\[0.8em] &= \frac{x^2+6x+4}{(x+3)^2} \end{align*}\]
oder
\[\begin{align*}f'(x) &= 1 + 5 \cdot (\textcolor{#0087c1}{-1}) \cdot \textcolor{#0087c1}{(\textcolor{#cc071e}{x+3})^{-2}} \cdot \textcolor{#cc071e}{1} \\[0.8em] &=1 - \frac{5}{(x+3)^2} \\[0.8em] & \enspace \, \vdots \\[0.8em] &= \frac{x^2+6x+4}{(x+3)^2}\end{align*}\]
\(x\)-Koordiante von \(T\)
Die notwendige Bedingung für eine Extremstelle von \(f\) lautet:
Extremstelle(n) bestimmen

Extremstelle(n) bestimmen mit Vorzeichenwechsel der 1. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#cc071e}{f'(x_0) = 0}\) ist und \(\textcolor{#cc071e}{f'}\) bei \(x_0\) einen Vorzeichenwechsel
von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{–}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
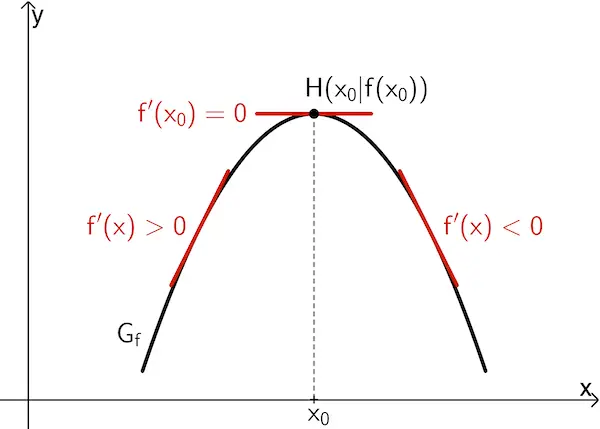
von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#cc071e}{+}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
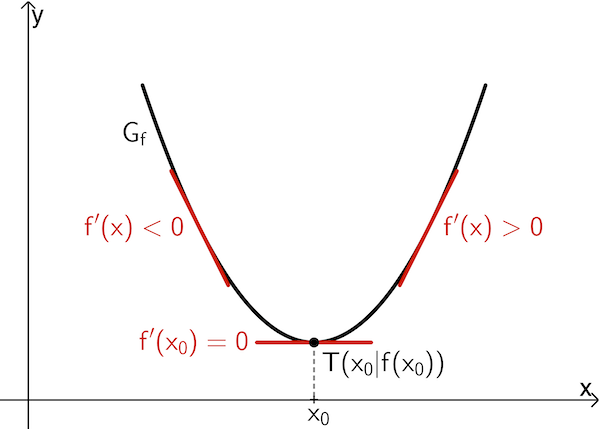
Extremstelle(n) bestimmen mit Vorzeichen der 2. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#cc071e}{\boldsymbol{<}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
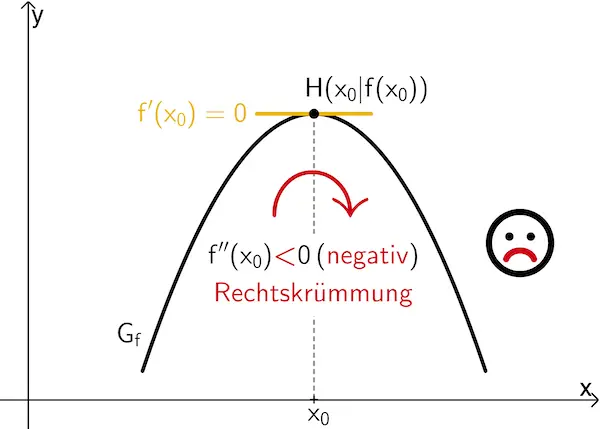
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#0087c1}{\boldsymbol{>}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
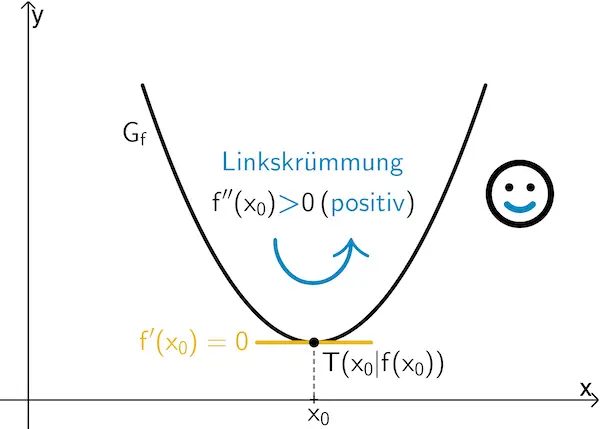
\[f'(x) = 0\]
Nullstelle(n) von \(f'\) bestimmen:
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
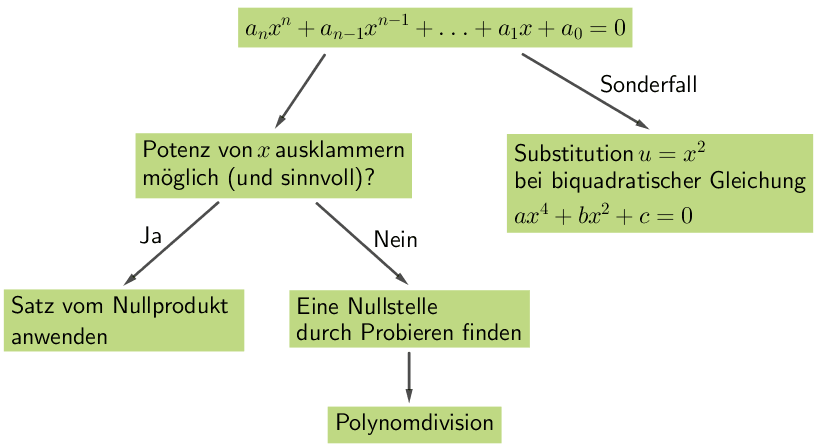
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
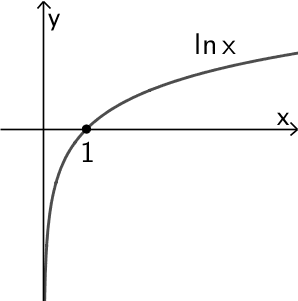
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
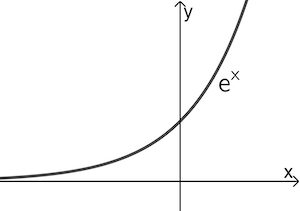
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[f'(x) = 0 \; \Rightarrow \; x^2+6x+4 = 0\]
Lösungsformel für quadratische Gleichungen (Mitternachtsformel) anwenden:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{1,2} &= \frac{-6 \pm \sqrt{6^2 - 4 \cdot 1 \cdot 4}}{2 \cdot 1} = \frac{-6 \pm 2\sqrt{5}}{2} = -3 \pm \sqrt{5} \end{align*}\]
\[x_1 = -3-\sqrt{5} \approx -5{,}24\]
\[x_2 = -3 +\sqrt{5} \approx -0{,}76\]
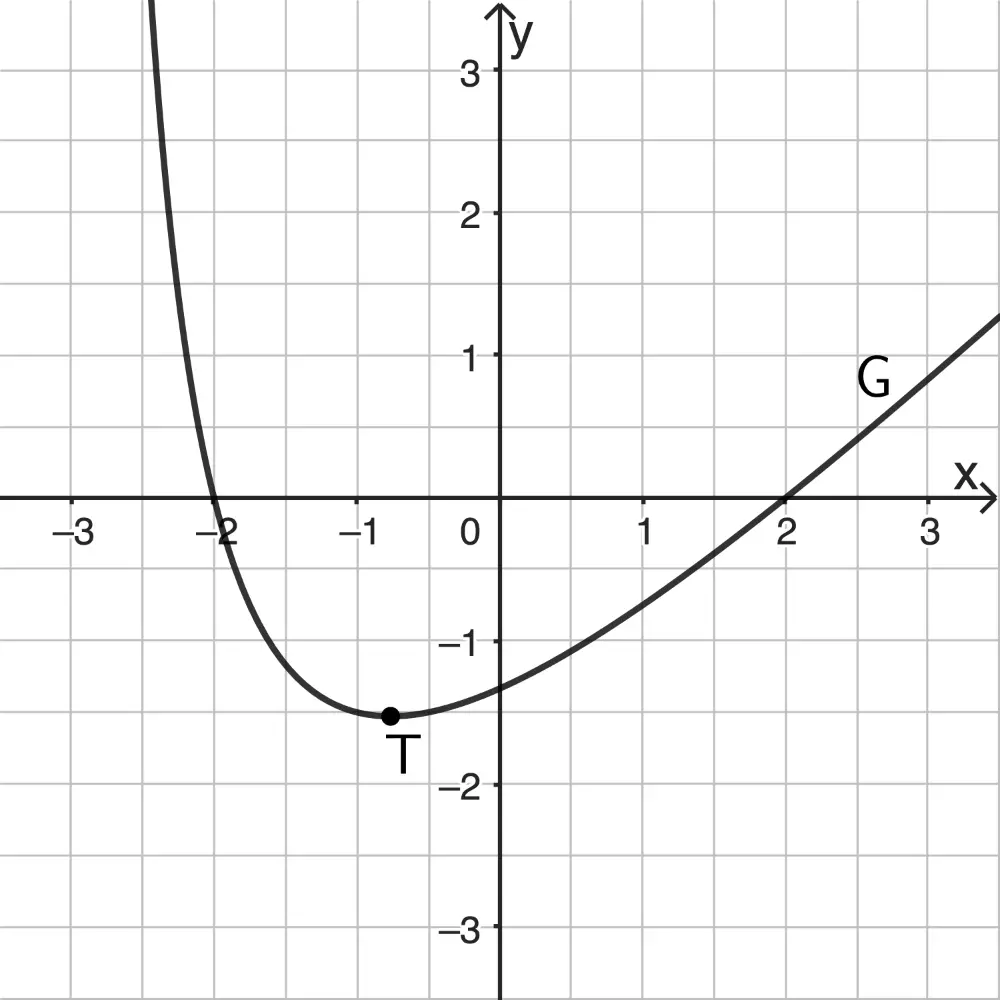
Die Abbildung zeigt, dass \(x = -3+\sqrt{5} \approx -0{,}76\) die \(x\)-Koordinate von \(T\) ist.


