Skizzieren Sie in Abbildung 1 einen möglichen Graphen von \(f\).
(3 BE)
Lösung zu Teilaufgabe 3b
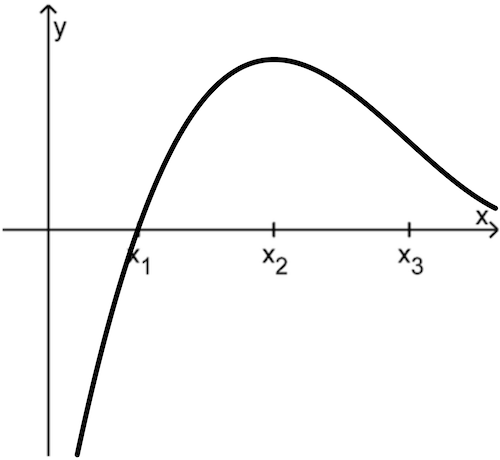 Abb. 1
Abb. 1
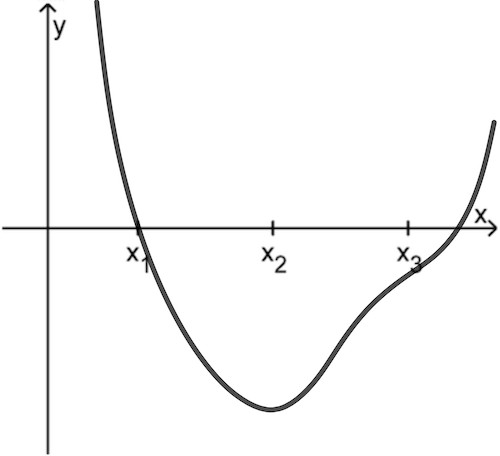 Abb. 1
Abb. 1
Mögliche Graphen von \(f\)
Ausführliche Erklärung (nicht verlangt)
Analyse der Eigenschaften:
- \(f\) hat bei \(x_1\) eine Nullstelle.
Der Graph der Funktion \(f\) schneidet oder berührt die \(x\)-Achse an der Stelle \(x_1\).
- Es gilt \(f'(x_2) = 0\) und \(f''(x_2) \neq 0\).
Mit \(f'(x_2) = 0\) hat der Graph der Funktion \(f\) an der Stelle \(x_2\) eine waagrechte Tangente. Da zugleich \(f''(x_2) \neq 0\) gilt, kann an der Stelle \(x_2\) kein Terrassenpunkt (Wendepunkt mit waagrechter Wendetangente) sein, sondern ausschließlich ein Extrempunkt.
- \(f'\) hat ein lokales Minimum an der Stelle \(x_3\).
\(x_3\) ist Wendestelle des Graphen der Funktion \(f\).
Für den Fall, dass der Graph in der Umgebung von \(x_3\) fällt, ist \(x_3\) eine Stelle der lokal stärksten Abnahme (Steigung ist maximal negativ).
Für den Fall, das der Graph in der Umgebung von \(x_3\) steigt, ist \(x_3\) eine Stelle der lokal geringsten Zunahme (Steigung ist minimal positiv).
Zwei mögliche Vorgehensweisen
1. Möglichkeit
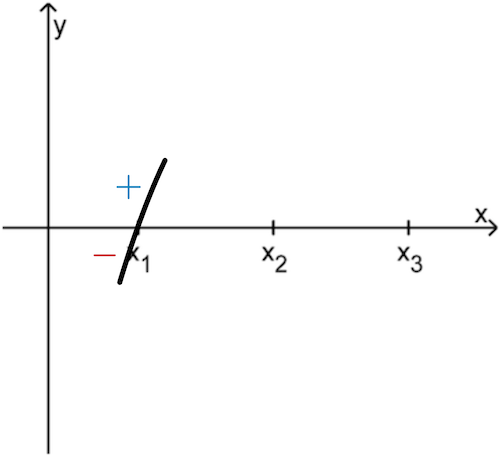 Abb. 1
Abb. 1
Der Graph der Funktion \(f\) schneidet die \(x\)-Achse an der Stelle \(x_1\) mit Vorzeichenwechsel von – nach + .
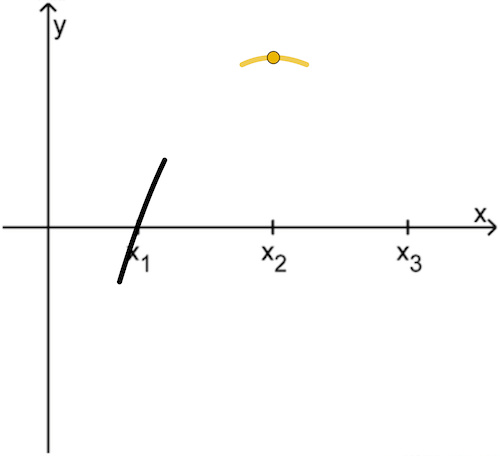 Abb. 1
Abb. 1
Dann besitzt der Graph von \(f\) an der Stelle \(\textcolor{#e9b509}{x_2}\) einen Hochpunkt ...
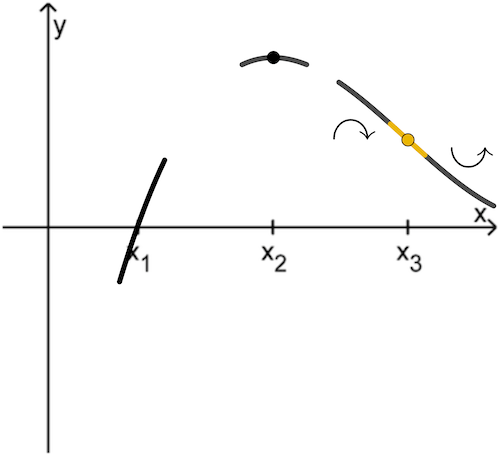 Abb. 1
Abb. 1
und im Wendepunkt an der Stelle \(\textcolor{#e9b509}{x_3}\) ist die Steigung des Graphen von \(f\) maximal negativ.
 Abb. 1
Abb. 1
Im dargestellten Bereich ergibt sich ein möglicher Graph einer ganzrationalen Funktion \(f\) vom Grad 3.
2. Möglichkeit
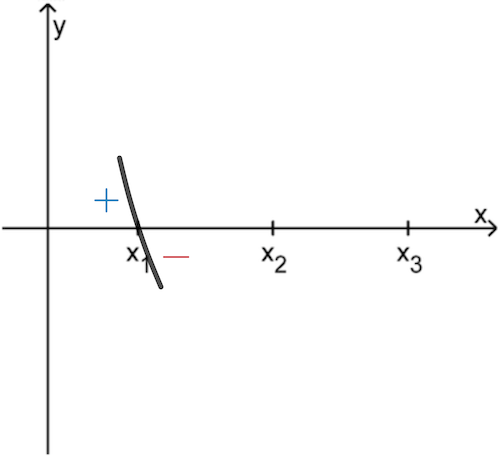 Abb. 1
Abb. 1
Der Graph der Funktion \(f\) schneidet die \(x\)-Achse an der Stelle \(x_1\) mit Vorzeichenwechsel von + nach –.
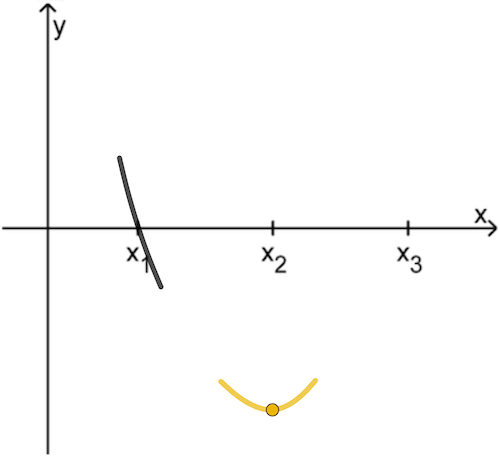 Abb. 1
Abb. 1
Dann besitzt der Graph von \(f\) an der Stelle \(\textcolor{#e9b509}{x_2}\) einen Tiefpunkt ...
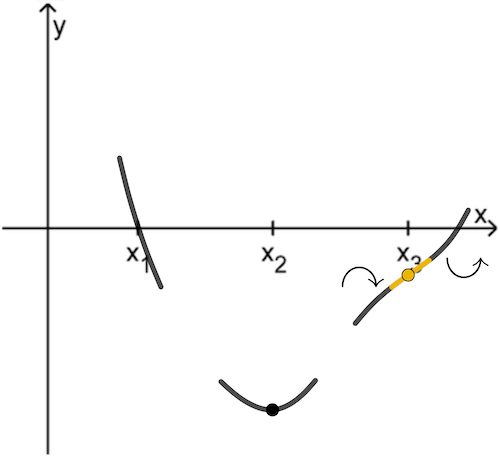 Abb. 1
Abb. 1
und im Wendepunkt an der Stelle \(\textcolor{#e9b509}{x_3}\) ist die Steigung des Graphen von \(f\) minimal positiv.
 Abb. 1
Abb. 1
Im dargestellten Bereich ergibt sich ein möglicher Graph einer ganzrationalen Funktion \(f\) vom Grad 4.

