Für ein Spiel wird ein Glücksrad verwendet, das drei farbige Sektoren hat. Der Tabelle können die Farben der Sektoren und die Größe der zugehörigen Mittelpunktswinkel entnommen werden.

Für einen Einsatz von 5 Euro darf ein Spieler das Glücksrad dreimal drehen. Erzielt der Spieler dreimal die gleiche Farbe, werden ihm 10 Euro ausgezahlt. Erzielt er drei verschiedene Farben, wird ein anderer Betrag ausgezahlt. In allen anderen Fällen erfolgt keine Auszahlung.
Die Wahrscheinlichkeit dafür, dass dreimal die gleiche Farbe erzielt wird, ist \(\frac{1}{6}\). Zeigen Sie, dass die Wahrscheinlichkeit dafür, dass drei verschiedene Farben erzielt werden, ebenfalls \(\frac{1}{6}\) beträgt.
(2 BE)
Lösung zu Teilaufgabe 2a
Entsprechend der Mittelpunktswinkel der Sektoren ergeben sich folgende Wahrscheinlichkeiten:
| Farbe | Blau | Rot | Grün |
| Mittelpunktswinkel | \(180^{\circ}\) | \(120^{\circ}\) | \(60^{\circ}\) |
| Wahrscheinlichkeit | \(\dfrac{180^{\circ}}{360^{\circ}} = \dfrac{1}{2}\) | \(\dfrac{120^{\circ}}{360^{\circ}} = \dfrac{1}{3}\) | \(\dfrac{60^{\circ}}{360^{\circ}} = \dfrac{1}{6}\) |
Veranschaulichung des Ereignisses „drei verschiedene Farben" mithilfe eines Baumdiagramms (nicht verlangt!):
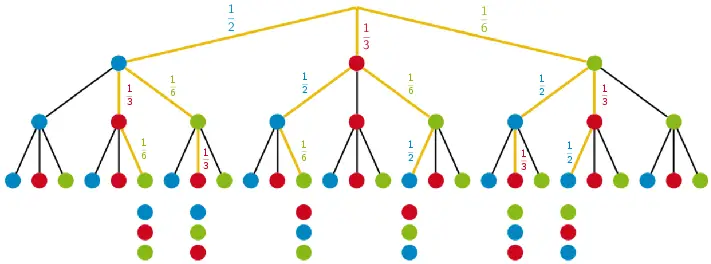
Es gibt mehrere Möglichkeiten für die Reihenfolge der drei verschiedenen Farben. Für die erste Farbe gibt es drei, für die zweite Farbe zwei Möglichkeiten und für die dritte Farbe noch eine Möglichkeit. Somit lassen sich die drei verschiedenen Farben auf \(3 \cdot 2 \cdot 1 = 3! = 6\) verschiedene Arten anordnen.
Mithilfe der 1. Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(\text{„3 verschiedene Farben"}) = 3! \cdot \textcolor{#0087c1}{\frac{1}{2}} \cdot \textcolor{#cc071e}{\frac{1}{3}} \cdot \textcolor{#89c117}{\frac{1}{6}} = \frac{1}{6}\]


