Abbildung 1 zeigt den Graphen \(G_f\) einer in \(\mathbb R\) definierten Funktion \(f\).
Skizzieren Sie in Abbildung 1 den Graphen der in \(\mathbb R\) definierten Integralfunktion \(\displaystyle F \colon x \mapsto \int_1^x f(t)\,dt\). Berücksichtigen Sie dabei mit jeweils angemessener Genauigkeit insbesondere die Nullstellen und Extremstellen von \(F\) sowie \(F(0)\).
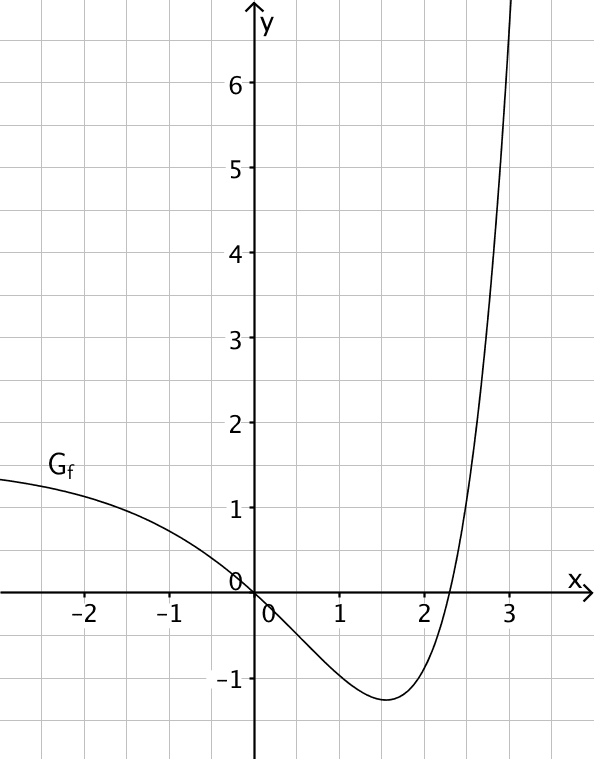 Abb. 1
Abb. 1
(6 BE)
Lösung zu Teilaufgabe 4
\[F(x) = \int_1^x f(t)\,dt\,; \quad D = \mathbb R \]
Nullstellen der Integralfunktion \(F\)
Erste Nullstelle der Integralfunktion \(F\):
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Die Integralfunktion \(F\) hat an der unteren Integrationsgrenze \(x = 1\) eine Nullstelle.
\[F(1) = \int_1^1 f(t)\,dt = 0\]
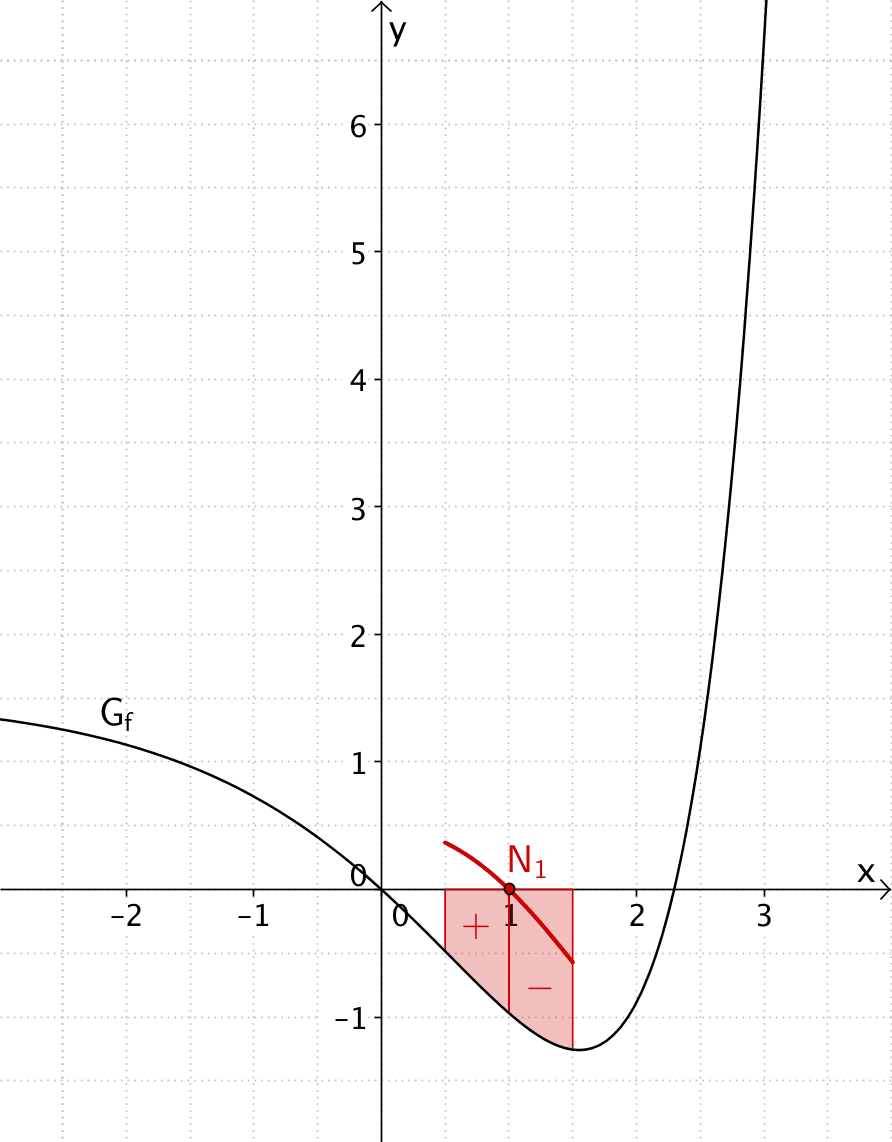
Verlauf des Graphen der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\) in der Nähe der ersten Nullstelle \(x_{N_1} = 1\)
Im Intervall \(]0;1[\) verläuft der Graph von \(f\) unterhalb der \(x\)-Achse. Der Wert des Integrals \(\displaystyle \int_1^x f(t\,dt)\) ist für \(x \in \; ]0;1[\) dennoch positiv, da „nach links" integriert wird (Der Wert der oberen Intergationsgrenze ist kleiner als der Wert der unteren Integrationsgrenze). Es gilt: \(\displaystyle \int_1^x f(t)\,dt = - \int_x^1 f(t)\,dt\)
\(\Longrightarrow \quad F(x) > 0\) für \(x \in \;]0;1[\)
Im Intervall \(]1; \approx 2{,}3[\) verläuft der Graph von \(f\) unterhalb der \(x\)-Achse. Der Wert des Integrals \(\displaystyle \int_1^x f(t)\,dt\) ist somit für \(x \in \; ]1; \approx 2{,}3[\) negativ.
\(\Longrightarrow \quad F(x) < 0\) für \(x \in \; ]1; \approx 2{,}3[\)
\(\Longrightarrow \quad\) An der Nullstelle \(x_{N_1}\) wechselt der Graph von \(F\) das Vorzeichen von \(+\) nach \(-\).
Die zweite und die dritte Nullstelle der Integralfunktion \(F\) lassen sich näherungsweise durch Abschätzen der Flächenbilanz ermitteln.
Zweite Nullstelle der Integralfunktion \(F\):
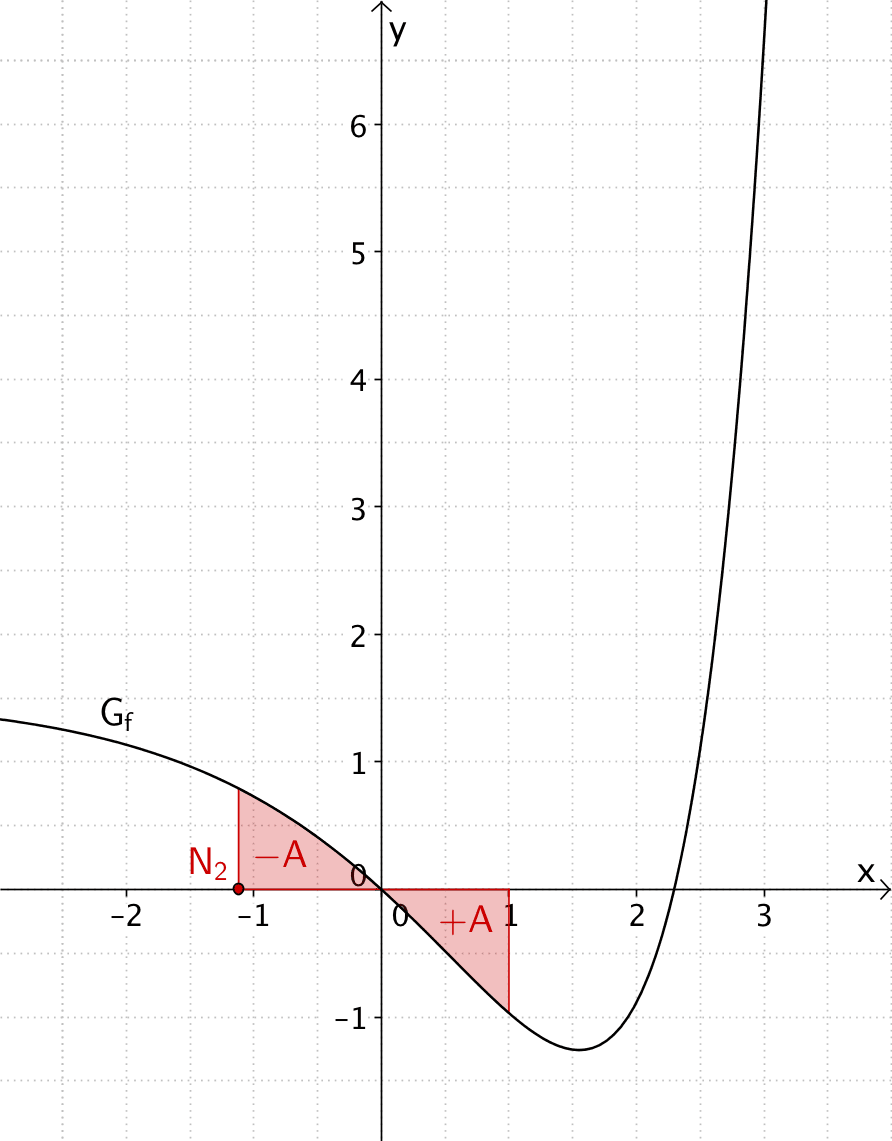
Zweite Nullstelle der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\,\): \(x_{N_2} \approx -1{,}1\)
Flächenbilanz - zweite Nullstelle:
Der Flächeninhalt des Flächenstücks, das \(G_f\) im Intervall \([0;1]\) mit der \(x\)-Achse einschließt, ist gleich dem Flächeninhalt des Flächenstücks, das \(G_f\) im Intervall \([\approx -1{,}1;0]\) mit der \(x\)-Achse einschließt.
Im Intervall \([0;1]\) zählt das Integral \(\displaystyle \int_1^x f(t)\,dt\) den Flächeninhalt positiv, da \(G_f\) zwar unterhalb der \(x\)-Achse verläuft, aber „nach links" integriert wird.
Im Intervall \([\approx -1{,}1;0]\) zählt das Integral \(\displaystyle \int_1^x f(t)\,dt\) den Flächeninhalt negativ, da \(G_f\) zwar oberhalb der \(x\)-Achse verläuft, aber „nach links" integriert wird.
\[\Longrightarrow \quad F(-1{,}1) = \int_1^{-1{,}1} f(t)\,dt \approx 0\]
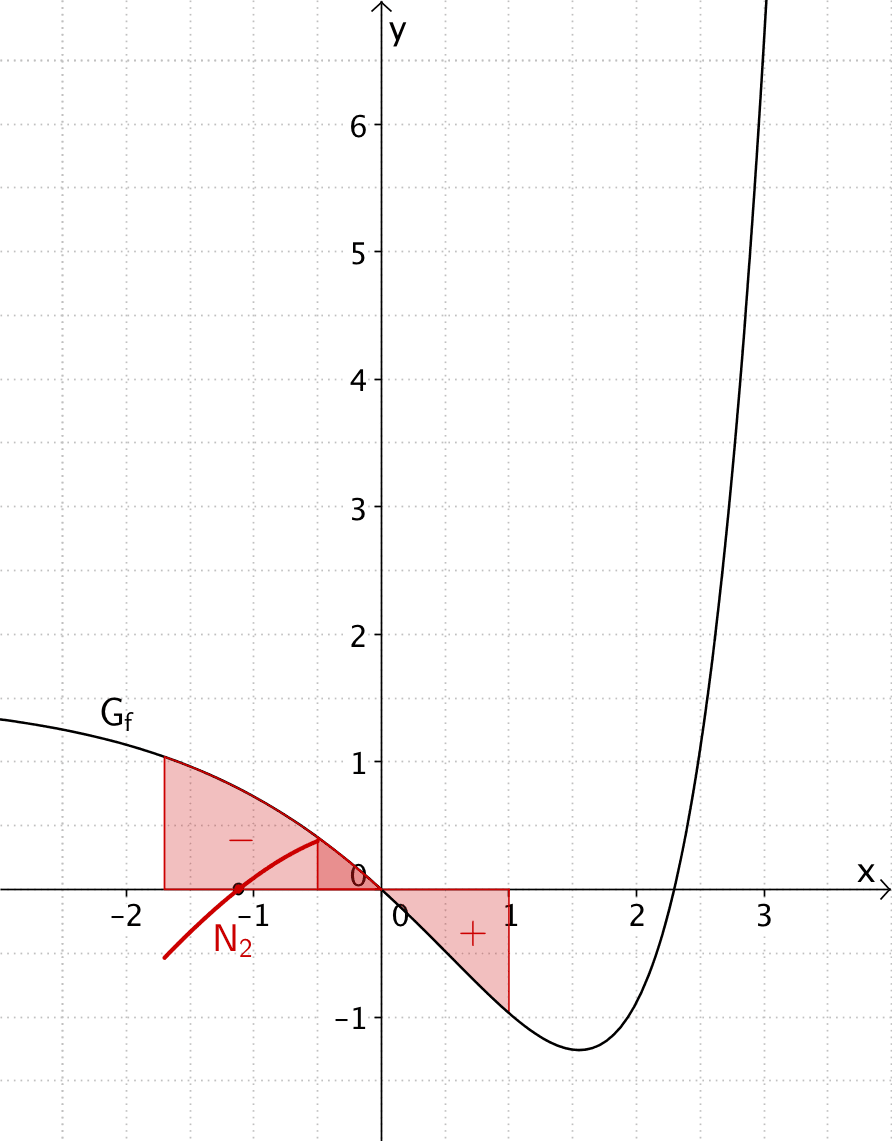
Verlauf des Graphen der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\) in der Nähe der zweiten Nullstelle \(x_{N_2} \approx -1{,}1\)
Für \(x \in \; ]\approx -1{,}1;0[\) ist die Flächenbilanz des Integrals \(\displaystyle \int_1^x f(t)\,dt\) positiv (im Bild für \(x = 0{,}5\) veranschaulicht), d.h. der Graph von \(F\) verläuft oberhalb der \(x\)-Achse.
\(F(x) > 0\) für \(x \in \; ]\approx -1{,}1;0[\)
Für \(x \lessapprox -1{,}1\) ist die Flächenbilanz des Integrals \(\displaystyle \int_1^x f(t)\,dt\) negativ (im Bild für \(x = -1{,}7\) veranschaulicht), d.h. der Graph von \(F\) verläuft unterhalb der \(x\)-Achse.
\(F(x) < 0\) für \(x \lessapprox -1{,}1\)
\(\Longrightarrow \quad\) An der Nullstelle \(x_{N_2}\) wechselt der Graph von \(F\) das Vorzeichen von \(-\) nach \(+\).
Dritte Nullstelle der Integralfunktion \(F\):
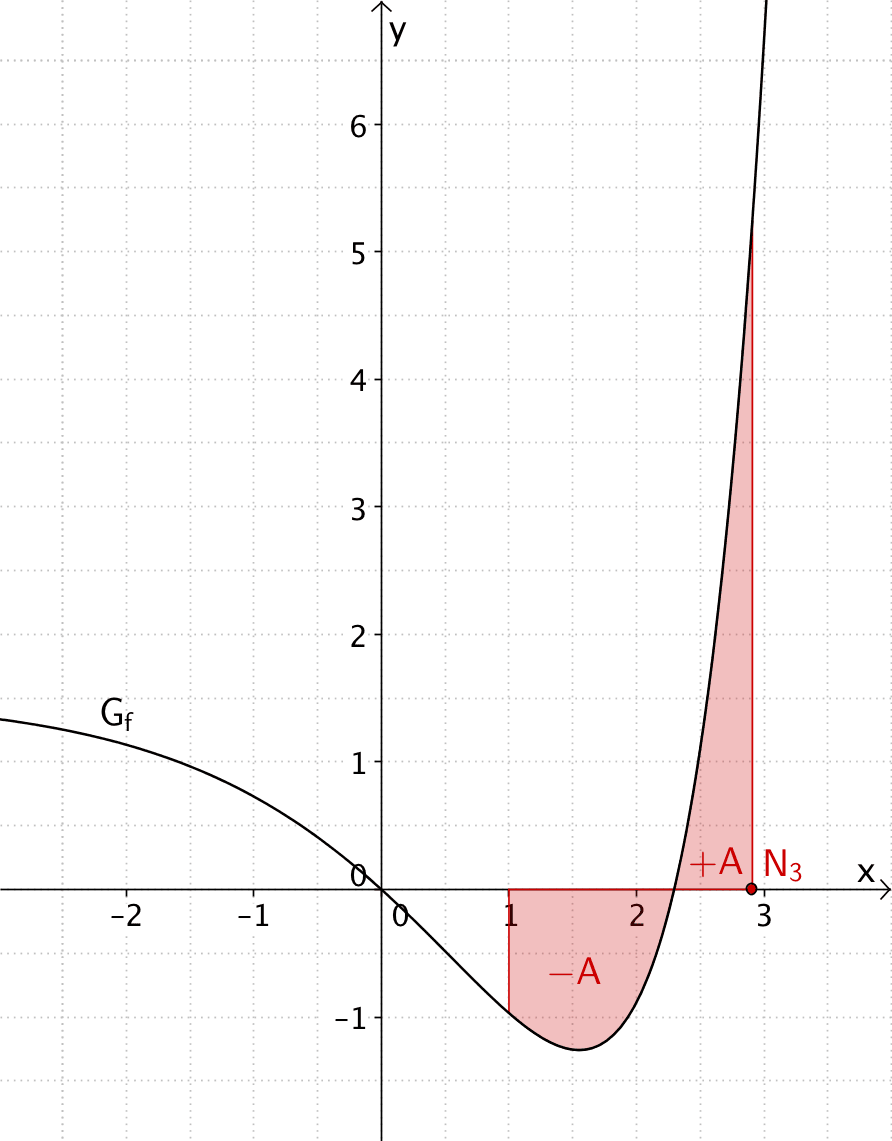
Dritte Nullstelle der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\,\): \(x_{N_3} \approx 2{,}9\)
Flächenbilanz - dritte Nullstelle:
Der Flächeninhalt des Flächenstücks, das \(G_f\) im Intervall \([1;\approx 2{,}3]\) mit der \(x\)-Achse einschließt, ist gleich dem Flächeninhalt des Flächenstücks, das \(G_f\) im Intervall \([\approx 2{,}3;\approx 2{,}9]\) mit der \(x\)-Achse einschließt.
Im Intervall \([1;\approx 2{,}3]\) zählt das Integral \(\displaystyle \int_1^x f(t)\,dt\) den Flächeninhalt negativ, da \(G_f\) unterhalb der \(x\)-Achse verläuft.
Im Intervall \([\approx 2{,}3; \approx2{,}9]\) zählt das Integral \(\displaystyle \int_1^x f(t)\,dt\) den Flächeninhalt positiv, da \(G_f\) oberhalb der \(x\)-Achse verläuft.
\[\Longrightarrow \quad F(2{,}9) = \int_1^{2{,}9} f(t)\,dt \approx 0\]
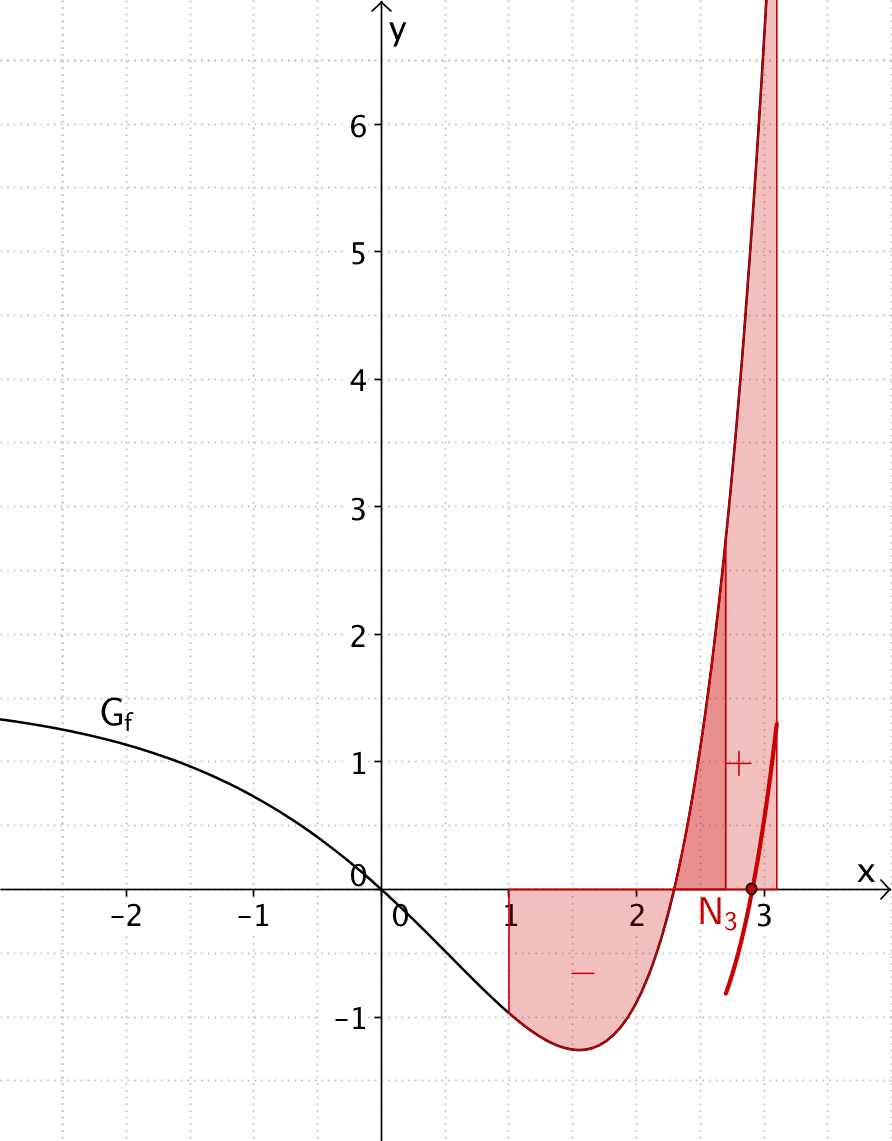
Verlauf des Graphen der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\) in der Nähe der dritten Nullstelle \(x_{N_3} \approx 2{,}9\)
Für \(x \in \; ]\approx 2{,}3; \approx 2{,}9[\) ist die Flächenbilanz des Integrals \(\displaystyle \int_1^x f(t)\,dt\) negativ (im Bild für \(x = 2{,}7\) veranschaulicht), d.h. der Graph von \(F\) verläuft unterhalb der \(x\)-Achse.
\(F(x) < 0\) für \(x \in \; ]\approx 2{,}3; \approx 2{,}9[\)
Für \(x \gtrapprox 2{,}9\) ist die Flächenbilanz des Integrals \(\displaystyle \int_1^x f(t)\,dt\) positiv (im Bild für \(x = 3{,}1\) veranschaulicht), d.h. der Graph von \(F\) verläuft oberhalb der \(x\)-Achse.
\(F(x) > 0\) für \(x \gtrapprox 2{,}9\)
\(\Longrightarrow \quad\) An der Nullstelle \(x_{N_3}\) wechselt der Graph von \(F\) das Vorzeichen von \(-\) nach \(+\).
Extremstellen der Integralfunktion \(F\)
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(x) = f(x)\]
Notwendige Bedingung für die Extremstellen der Integralfunktion \(F\):
\[F'(x) = f(x) \overset{!}{=} 0\]
\(\Longrightarrow \quad\) Die Nullstellen der Funktion \(f\) sind die Extremstellen der Integralfunktion \(F\).
Erste Extremstelle der Integralfunktion \(F\):
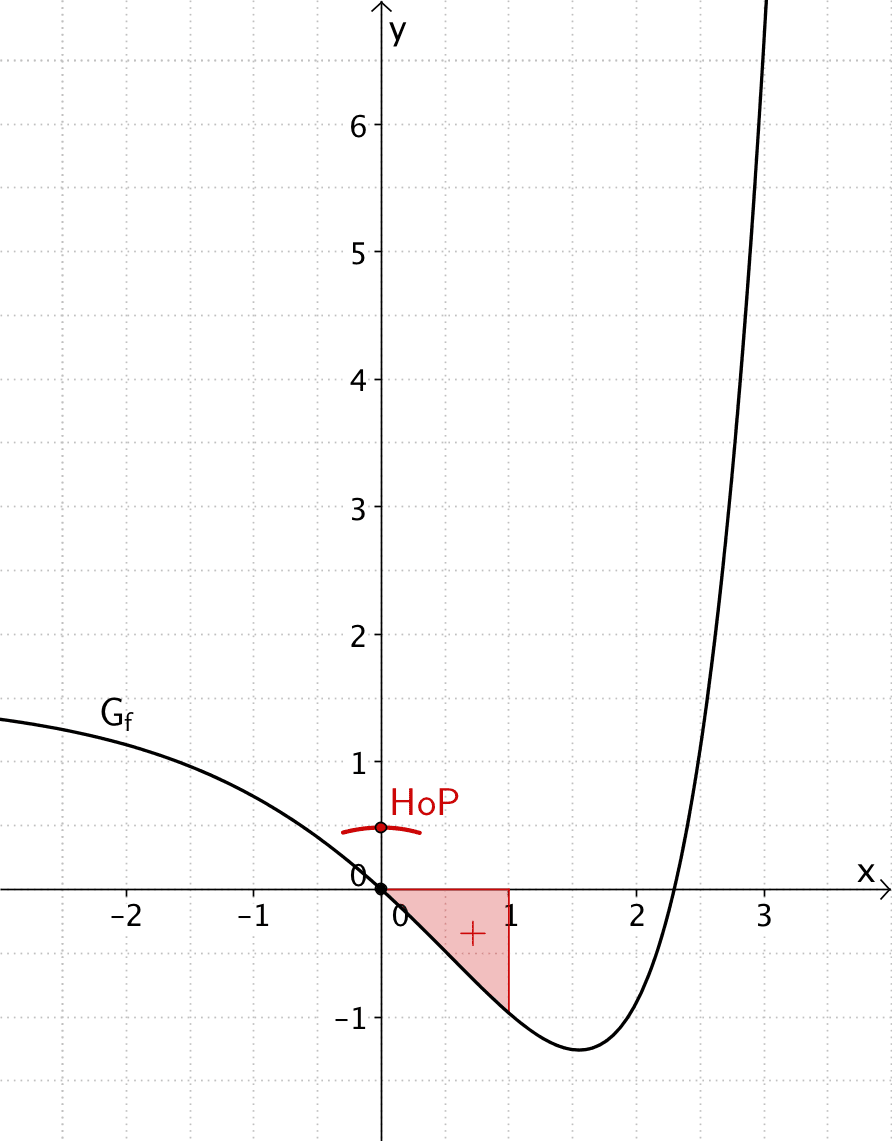
Erste Extremstelle der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\):
\[F'(0) = f(0) = 0\]
Der Graph von \(f\) hat an der Stelle \(x = 0\) eine einfache Nullstelle mit Vorzeichenwechsel von \(+\) nach \(-\). Demnach ändert der Graph von \(F\) das Monotieverhalten von „streng monoton steigend" zu „streng monoton fallend".
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &F'(x) > 0 \enspace \text{für} \enspace x < 0 \\ &F'(0) = 0 \\ &F'(x) < 0 \enspace \text{für} \enspace x > 0 \end{align*} \right \} \enspace \Rightarrow \enspace \text{Hochpunkt} \; HoP\,(0|F(0))\]
Der Wert für \(\displaystyle F(0) = \int_1^0 f(t)\,dt\) lässt sich näherungsweise bestimmen, indem man den Flächeninhalt des Flächenstücks abschätzt, das der Graph von \(f\) im Intervall \([0;1]\) mit der \(x\)-Achse einschließt. Das Integral \(\displaystyle \int_1^0 f(t)\,dt\) zählt den Flächeninhalt positiv, da \(G_f\) zwar unterhalb der \(x\)-Achse verläuft, aber „nach links" integriert wird.
Der Flächeninhalt entsprich ungefähr dem Flächeninhalt von zwei Kästchen (\(0{,}5^2\) FE).
\[2 \cdot 0{,}5^2 = 0{,}5\]
\[\Longrightarrow \quad F(0) = \int_1^0 f(t)\,dt \approx 0{,}5\]
\[\Longrightarrow \quad HoP \,(0|0{,}5)\]
Zweite Extremstelle der Integralfunktion \(F\):
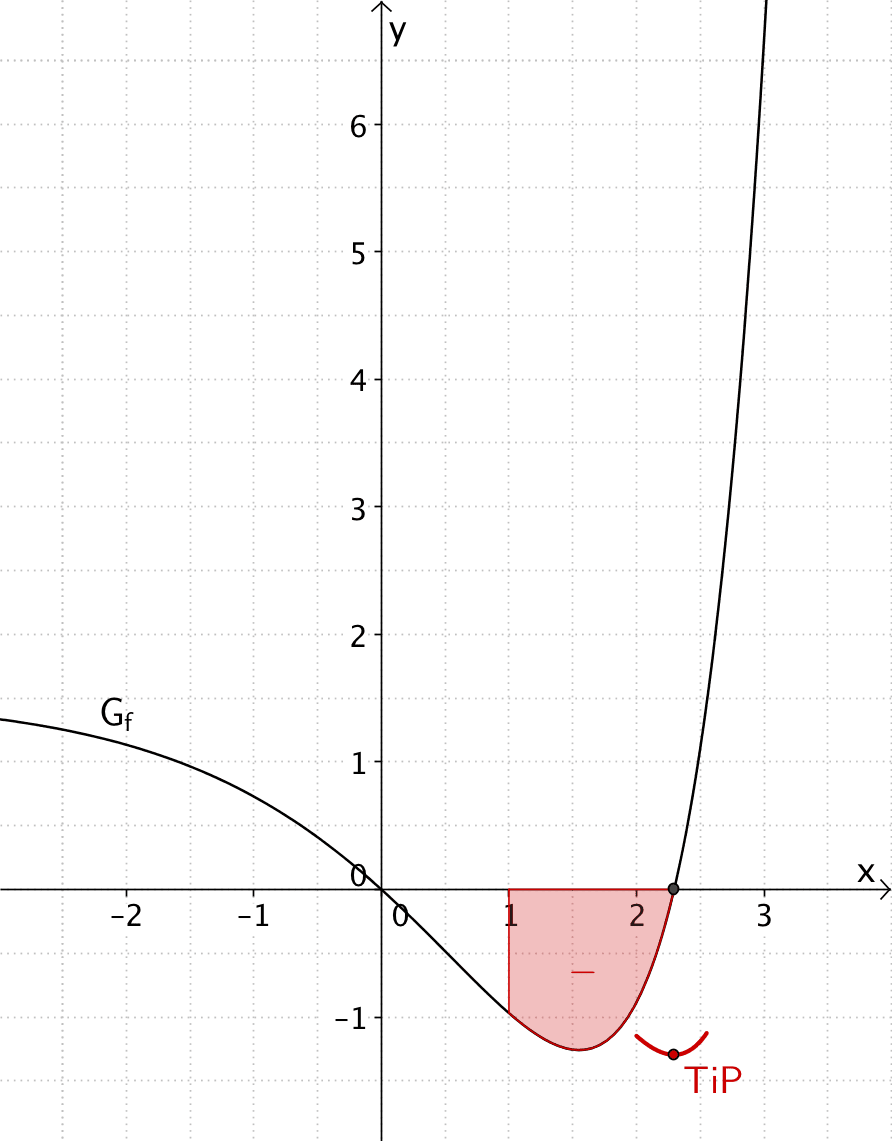
Zweite Extremstelle der Integralfunktion \(\displaystyle F(x) = \int_1^x f(t)\,dt\):
\[F'(2{,}3) = f(2{,}3) \approx 0\]
Der Graph von \(f\) hat an der Stelle \(x \approx 2{,}3\) eine einfache Nullstelle mit Vorzeichenwechsel von \(-\) nach \(+\). Demnach ändert der Graph von \(F\) das Monotieverhalten von „streng monoton fallend" zu „streng monoton steigend".
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &F'(x) < 0 \enspace \text{für} \enspace x \lessapprox 2{,}3 \\ &F'(2{,}3) \approx 0 \\ &F'(x) > 0 \enspace \text{für} \enspace x \gtrapprox 2{,}3 \end{align*} \right \} \enspace \Rightarrow \enspace \text{Tiefpunkt} \; TiP\,(2{,}3|F(2{,}3))\]
Der Wert für \(\displaystyle F(2{,}3) = \int_1^{2{,}3} f(t)\,dt\) lässt sich näherungsweise bestimmen, indem man den Flächeninhalt des Flächenstücks abschätzt, das der Graph von \(f\) im Intervall \([1;2{,}3]\) mit der \(x\)-Achse einschließt. Das Integral \(\displaystyle \int_1^{2{,}3} f(t)\,dt\) zählt den Flächeninhalt negativ, da \(G_f\) unterhalb der \(x\)-Achse verläuft.
Der Flächeninhalt entsprich ungefähr dem Flächeninhalt von fünf Kästchen (\(0{,}5^2\) FE).
\[5 \cdot 0{,}5^2 = 1{,}25\]
\[\Longrightarrow \quad F(2{,}3) = \int_1^{2{,}3} f(t)\,dt \approx -1{,}25\]
\[\Longrightarrow \quad TiP \,(2{,}3|-1{,}25)\]
Zusammenfassung und Skizze des Graphen der Integralfunktion \(F\)
\[F(1) = 0\,, \quad F(-1{,}1) \approx 0\,, \quad F(2{,}9) \approx 0\]
\[HoP\,(0|0{,}5)\,, \quad TiP\,(2{,}3|-1{,}25)\]
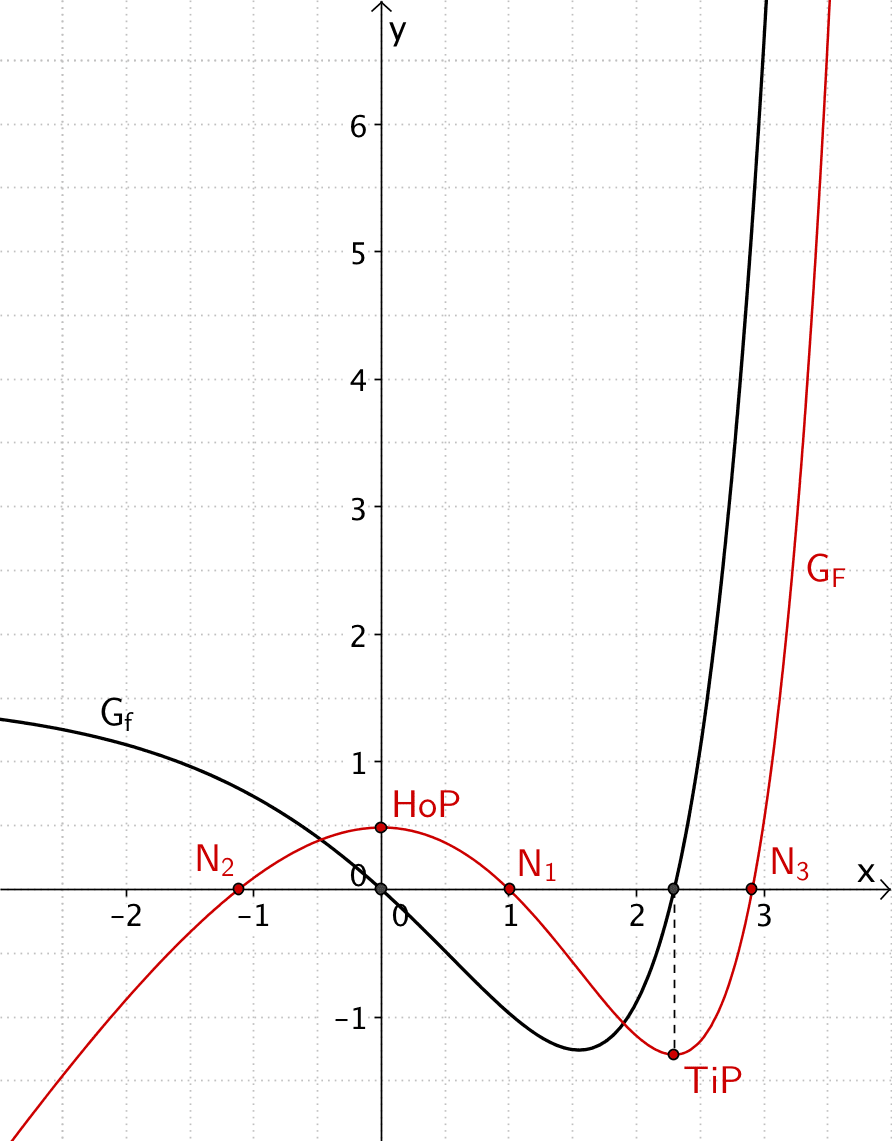
Skizze des Graphen der Integralfunktion \(F\)


