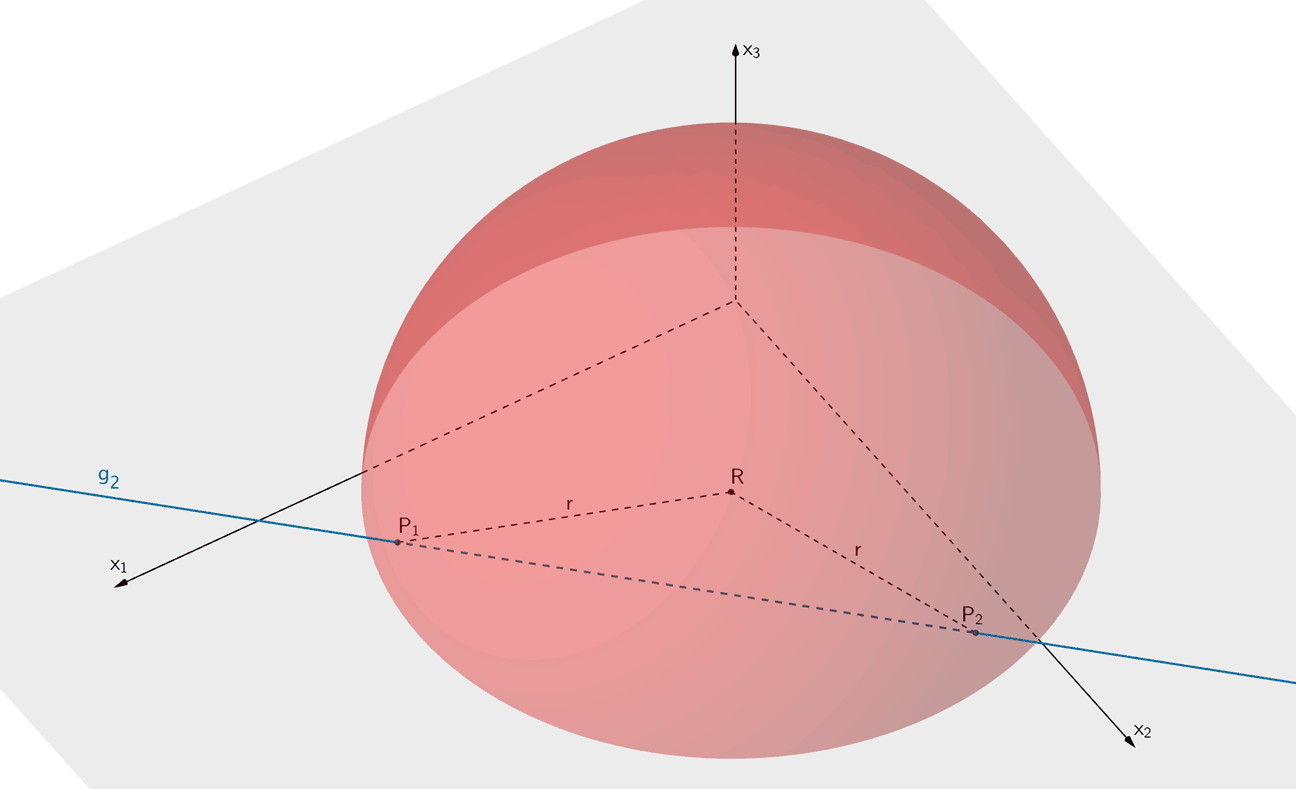
Eine Radarstation, deren Position im Modell durch den Punkt \(R\,(20|30|0)\) veranschaulicht wird, erfasst alle Objekte im Luftraum bis zu einer Entfernung von 50 km. Berechnen Sie die Länge der Flugstrecke von \(F_2\) in dem vom Radar erfassten Bereich.
(6 BE)
Lösung zu Teilaufgabe e
1. Lösungsansatz: Betrag eines Vektors / Länge einer Strecke
2. Lösungsansatz: Schnittpunkte einer Geraden mit einer Kugel
3. Lösungsansatz: Abstand Punkt - Gerade, Satz des Pythagoras
3. a) Abstand \(d(R;g_2)\) - Ansatz mit Hilfsebene
3. b) Abstand \(d(R;g_2)\) - Anwenden des Skalarprodukts
Der Überwachungsbereich des Radars beschreibt auf der \(x_1x_2\)-Ebene eine Halbkugel mit dem Mittelpunkt \(R\) und dem Radius \(r = 50\). Die Flugbahn des Flugzeugs \(F_2\) entlang der Geraden \(g_2\) verläuft mit der konstanten Flughöhe 10 km (siehe Teilaufgabe 1a). Überfliegt \(F_2\) den Überwachungsbereich, gibt es einen Eintrittspunkt \(P_1\) und einen Austrittspunkt \(P_2\). Die Länge der Strecke \([P_1P_2]\) entspricht der Länge der Flugstrecke von \(F_2\) im Überwachungsbereich des Radars.
Flugbahn von \(F_2\):
\[g_2\colon \enspace \overrightarrow X = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix},\enspace \mu \in \mathbb R\]
\(R\,(20|30|0)\)
Überwachungsradius: \(\,r = 50\; \text{km}\)
1. Lösungsansatz: Betrag eines Vektors / Länge einer Strecke
Bedingung:
Die Länge der Strecke \([RP]\) zwischen dem Punkt \(R\) und einem Punkt \(P \in g_{2}\) ist gleich dem Radius \(r\) der Halbkugel (Überwachungsradius des Radars).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{RP} &= r \\[0.8em] \vert \overrightarrow{RP} \vert &= 50 \\[0.8em] \vert \overrightarrow{P} - \overrightarrow{R} \vert &= 50 & &| P \in g_{2} \\[0.8em] \left| \begin {pmatrix} 40 + 10 \mu \\ 50 - 10 \mu \\ 10 \end {pmatrix} - \begin {pmatrix} 20 \\ 30 \\ 0 \end {pmatrix} \right| &= 50 \\[0.8em] \left| \begin {pmatrix} 20 + 10 \mu \\ 20 - 10 \mu \\ 10 \end {pmatrix} \right| &= 50 \\[0.8em] \sqrt{(20 + 10 \mu)^2 + (20 - 10 \mu)^2 + 10^2} &= 50 \\[0.8em] \sqrt{400 + 400 \mu + 100 \mu^2 + 400 - 400 \mu + 100 \mu^2 + 100} &= 50 \\[0.8em] \sqrt{900 + 200 \mu^2} &= 50 & &| (\dots)^{2} \\[0.8em] 900 + 200\mu^2 &= 2500 & &| - 900 \\[0.8em] 200\mu^{2} &= 1600 & &| : 200 \\[0.8em] \mu^{2} &= 8 & & | \;\sqrt{\quad} \\[0.8em] \mu_{1,2} &= \pm 2\sqrt{2} \end{align*}\]
Koordinaten der Punkte \(P_1\) und \(P_2\) berechnen:
\[P_1 \in g_2\, \colon \, \overrightarrow {P_{1}} = \begin{pmatrix} 40 \\ 50 \\ 10 \end{pmatrix} + 2\sqrt{2} \cdot \begin{pmatrix} 10\\ -10 \\ 0 \end{pmatrix} = \begin{pmatrix} 40 + 20 \sqrt 2 \\ 50 - 20 \sqrt 2 \\ 10 \end{pmatrix}\]
\[P_2 \in g_2\, \colon \, \overrightarrow {P_{2}} = \begin{pmatrix} 40 \\ 50 \\ 10 \end{pmatrix} - 2\sqrt{2} \cdot \begin{pmatrix} 10\\ -10 \\ 0 \end{pmatrix} = \begin {pmatrix} 40 - 20 \sqrt 2 \\ 50 + 20 \sqrt 2 \\ 10 \end {pmatrix}\]
Länge der Strecke \([P_1P_2]\) berechnen:
\[ \begin {align*} \overline{P_1P_2} &= \vert \overrightarrow{P_1P_2} \vert \\[0.8em] &= \vert \overrightarrow {P_{2}} - \overrightarrow {P_{1}} \vert \\[0.8em] &= \left| \begin {pmatrix} 40 - 20 \sqrt 2 \\ 50 + 20 \sqrt 2 \\ 10 \end {pmatrix} - \begin {pmatrix} 40 + 20 \sqrt 2 \\ 50 - 20 \sqrt 2 \\ 10 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} -40 \sqrt 2 \\ 40 \sqrt 2 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \sqrt{(-40 \sqrt 2)^2 + (40 \sqrt 2)^2} \\[0.8em] &= \sqrt{6400} \\[0.8em] &= 80 \end {align*} \]
Die Länge der Flugstrecke von \(F_2\) im Überwachungsbereich des Radars beträgt 80 km.
2. Lösungsansatz: Schnittpunkte einer Geraden mit einer Kugel
Es sei \(K\) die Kugel mit dem Mittelpunkt \(R\,(20|30|0)\) und dem Radius \(r = 50\), deren Halbkugel über der \(x_1x_2\)-Ebene den Überwachungsbereich des Radars beschreibt.
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[\begin{align*} K\, \colon \, (x_1 - 20)^2 + (x_2 - 30)^2 + (x_3 - 0)^2 &= 50^2 \\[0.8em] (x_1 - 20)^2 + (x_2 - 30)^2 + {x_3}^2 &= 2500 \end{align*}\]
\[g_2\,\colon \, \overrightarrow X = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix}\]
\[\begin{align*} g_2 \cap K\, \colon \, (40 + 10\mu - 20)^2 + (50 - 10\mu - 30)^2 + {10}^2 &= 2500 \\[0.8em] (20 + 10\mu)^2 + (20 - 10\mu)^2 + {10}^2 &= 2500 \\[0.8em] 400 + 400 \mu + 100 \mu^2 + 400 - 400 \mu + 100 \mu^2 + 100 &= 2500 \\[0.8em] 900 + 200{\mu}^2 &= 2500 & &| - 900 \\[0.8em] 200\mu^{2} &= 1600 & &| : 200 \\[0.8em] {\mu}^2 &= 8 & &| \; \sqrt{\quad} \\[0.8em] \mu_{1,2} &= \pm 2\sqrt{2} \end{align*}\]
Koordinaten der Punkte \(P_1\) und \(P_2\) berechnen:
\[P_1 \in g_2\, \colon \, \overrightarrow {P_{1}} = \begin{pmatrix} 40 \\ 50 \\ 10 \end{pmatrix} + 2\sqrt{2} \cdot \begin{pmatrix} 10\\ -10 \\ 0 \end{pmatrix} = \begin{pmatrix} 40 + 20 \sqrt 2 \\ 50 - 20 \sqrt 2 \\ 10 \end{pmatrix}\]
\[P_2 \in g_2\, \colon \, \overrightarrow {P_{2}} = \begin{pmatrix} 40 \\ 50 \\ 10 \end{pmatrix} - 2\sqrt{2} \cdot \begin{pmatrix} 10\\ -10 \\ 0 \end{pmatrix} = \begin {pmatrix} 40 - 20 \sqrt 2 \\ 50 + 20 \sqrt 2 \\ 10 \end {pmatrix}\]
Länge der Strecke \([P_1P_2]\) berechnen:
\[ \begin {align*} \overline{P_1P_2} &= \vert \overrightarrow{P_1P_2} \vert \\[0.8em] &= \vert \overrightarrow {P_{2}} - \overrightarrow {P_{1}} \vert \\[0.8em] &= \left| \begin {pmatrix} 40 - 20 \sqrt 2 \\ 50 + 20 \sqrt 2 \\ 10 \end {pmatrix} - \begin {pmatrix} 40 + 20 \sqrt 2 \\ 50 - 20 \sqrt 2 \\ 10 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} -40 \sqrt 2 \\ 40 \sqrt 2 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \sqrt{(-40 \sqrt 2)^2 + (40 \sqrt 2)^2} \\[0.8em] &= \sqrt{6400} \\[0.8em] &= 80 \end {align*} \]
Die Länge der Flugstrecke von \(F_2\) im Überwachungsbereich des Radars beträgt 80 km.
3. Lösungsansatz: Abstand Punkt - Gerade, Satz des Pythagoras
Man bestimmt zunächst den Abstand \(d(R;g_2)\) zwischen dem Punkt \(R\) und der Geraden \(g_2\). Anschließend berechnet man mithilfe des Satzes des Pythagoras die Länge der Strecke \([P_1P_2]\).
a) Abstand \(d(R;g_2)\) - Ansatz mit Hilfsebene
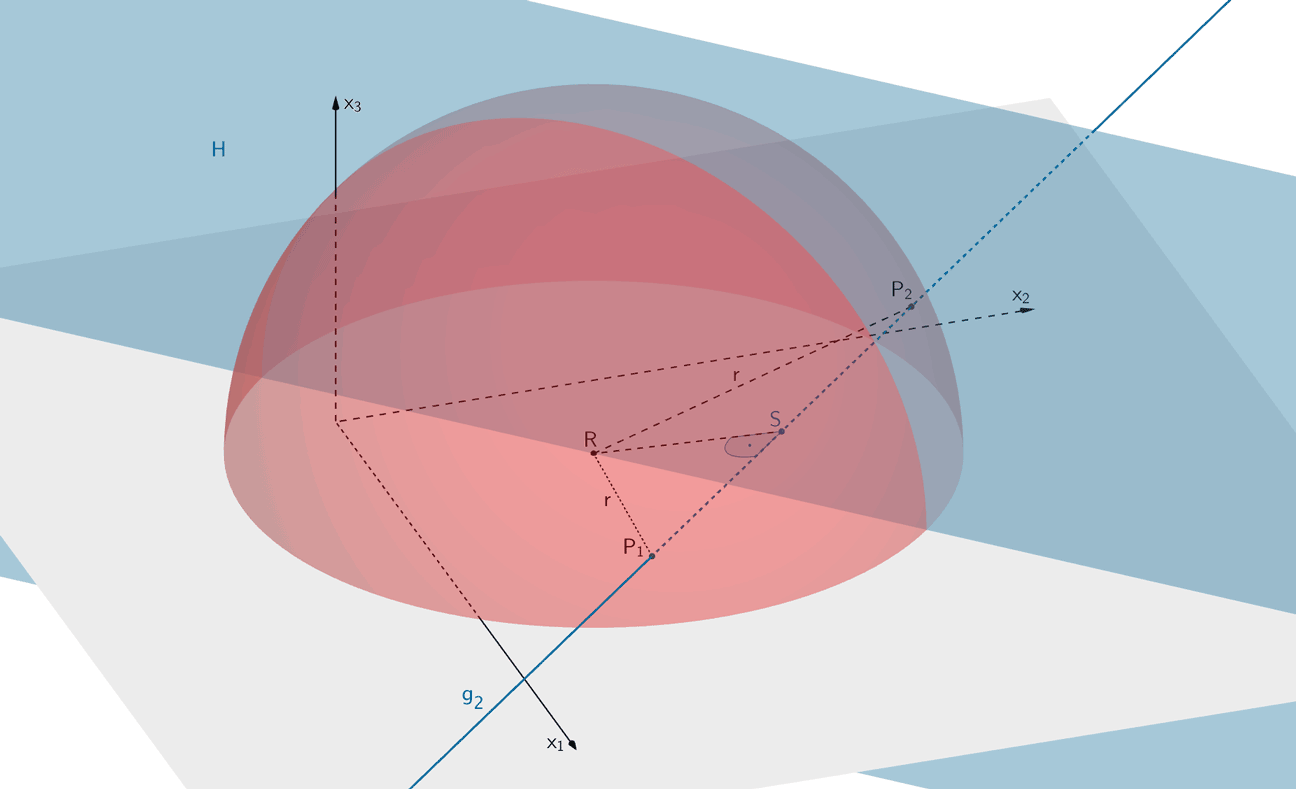
Die Hilfsebene \(H\) enthält den Punkt \(R\) und ist senkrecht zur Geraden \(g_2\). Sie schneidet die Gerade \(g_2\) im Punkt \(S\). Der Abstand \(d(R;g_2)\) des Punktes \(R\) von der Geraden \(g_2\) ist gleich der Länge der Strecke \([RS]\).
Hilfsebene \(H\) mit den Eigenschaften \(R \in H\) und \(H \perp g_2\) bestimmen:
Abstand Punkt - Gerade, Ansatz: Hilfsebene aufstellen
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
1. Hilfsebene \(H\) mit den Eigenschaften \(P \in H\) und \(H \perp g\) bestimmen:
\[H \colon \overrightarrow{n}_H \circ \left( \overrightarrow X - \overrightarrow P \right) = 0\,; \quad \overrightarrow{n}_H = \overrightarrow u\]
2. Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g\) ermitteln:
\(H \cap g \colon \overrightarrow{n}_H \circ \left( \overrightarrow A + \lambda \cdot \overrightarrow u - \overrightarrow P \right) = 0 \quad \Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[S \in g \colon \overrightarrow S = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([PS]\) berechnen:
\[d\,(P; g) = \overline{PS} = \vert \overrightarrow P - \overrightarrow S \vert\]
\[g_2\, \colon \, \overrightarrow X = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix}\,,\enspace \mu \in \mathbb R\]
\[R\,(20|30|0)\]
\[\overrightarrow {u}_{g_2} = \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix} = 10 \cdot \begin {pmatrix} 1 \\ -1 \\ 0 \end {pmatrix} \quad \Longrightarrow \quad \overrightarrow {n}_H = \begin {pmatrix} 1 \\ -1 \\ 0 \end {pmatrix}\]
\[\begin{align*}H\,\colon & & \overrightarrow{n}_{H} \circ \left( \overrightarrow{X} - \overrightarrow{R} \right) &= 0 \\[0.8em] & & \begin {pmatrix} 1 \\ -1 \\ 0 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 20 \\ 30 \\ 0 \end {pmatrix} \right] &= 0 \end{align*}\]
Schnittpunkt \(S\) der Ebene \(H\) mit der Geraden \(g_2\) ermitteln:
Zur Berechnung des Schnittpunktes \(S\) setzt man den Ortsvektor \(\overrightarrow X\) aus der Geradengleichung von \(g_2\) in die Normalengleichung der Hilfsebene \(H\) ein und löst die Gleichung nach dem Parameter \(\mu\) auf.
\[g_2\,\colon \, \overrightarrow X = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix}\]
\[H\,\colon \, \begin {pmatrix} 1 \\ -1 \\ 0 \end {pmatrix} \circ \left[ \overrightarrow X - \begin {pmatrix} 20 \\ 30 \\ 0 \end {pmatrix} \right] = 0\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[ \begin {align*} g_2 \cap H \, \colon \, \begin {pmatrix} 1 \\ -1 \\ 0 \end {pmatrix} \circ \left[ \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix} - \begin {pmatrix} 20 \\ 30 \\ 0 \end {pmatrix} \right] &= 0 \\[0.8em] \begin {pmatrix} 1 \\ -1 \\ 0 \end {pmatrix} \circ \left[ \begin {pmatrix} 20 \\ 20 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix} \right] &= 0 \\[0.8em] 1 \cdot (20 + 10 \mu) + (-1) \cdot (20 - 10 \mu) &= 0 \\[0.8em] 20\mu &= 0 \\[0.8em] \mu &= 0 \end{align*}\]
Parameterwert \(\mu = 0\) in die Geradengleichung von \(g_2\) einsetzen:
\[S \in g_2\, \colon \, \overrightarrow S = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + 0 \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix} = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} \]
Länge der Strecke \([RS]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[R\,(20|30|0)\,,\enspace S\,(40|50|10)\]
\[ \begin {align*} \overline{RS} &= \vert \overrightarrow{RS} \vert \\[0.8em] &= \vert \overrightarrow S - \overrightarrow R \vert \\[0.8em] &= \left| \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} - \begin {pmatrix} 20 \\ 30 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 20 \\ 20 \\ 10 \end {pmatrix} \right| \\[0.8em] &= \sqrt{20^2 + 20^2 + 10^2} \\[0.8em] &= \sqrt{900} \\[0.8em] &= 30 \end {align*} \]
\[\Longrightarrow \quad d(R;g_2) = 30\]
Länge der Strecke \([P_1P_2]\) berechnen:
![Berechnung der Länge der Strecke [P₁P₂] mithilfe des Satzes des Pythagoras Berechnung der Länge der Strecke [P₁P₂] mithilfe des Satzes des Pythagoras](/images/stories/B2014BA_PT_B_G_1/B2014BA_PT_B_G_1_e_03.png)
Die Länge der Strecke \([P_1P_2]\) lässt sich mithilfe des Satzes des Pythagoras berechnen.
\[\begin{align*} \left( \frac{\overline{P_1P_2}}{2} \right)^2 + \overline{RS}^2 &= r^2 & &| -\overline{RS}^2 \\[0.8em] \frac{\overline{P_1P_2}^2}{4} &= r^2 - \overline{RS}^2 & &| \cdot 4 \\[0.8em] \overline{P_1P_2}^2 &= 4 \left( r^2 - \overline{RS}^2 \right) & &| \; \sqrt{\quad} \\[0.8em] \overline{P_1P_2} &= 2 \sqrt{r^2 - \overline{RS}^2} \\[0.8em] &= 2 \sqrt{50^2 - 30^2} \\[0.8em] &= 80 \end{align*}\]
Die Länge der Flugstrecke von \(F_2\) im Überwachungsbereich des Radars beträgt 80 km.
b) Abstand \(d(R;g_2)\) - Anwenden des Skalarprodukts
\[g_2\, \colon \, \overrightarrow X = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + \mu \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix}\,,\enspace \mu \in \mathbb R\]
\[R\,(20|30|0)\]
Abstand Punkt - Gerade, Ansatz: Skalarprodukt anwenden
\[P\,(p_1|p_2|p_3)\,, \quad g \colon \overrightarrow X = \overrightarrow A + \lambda \cdot \overrightarrow u\,; \quad \lambda \in \mathbb R\]
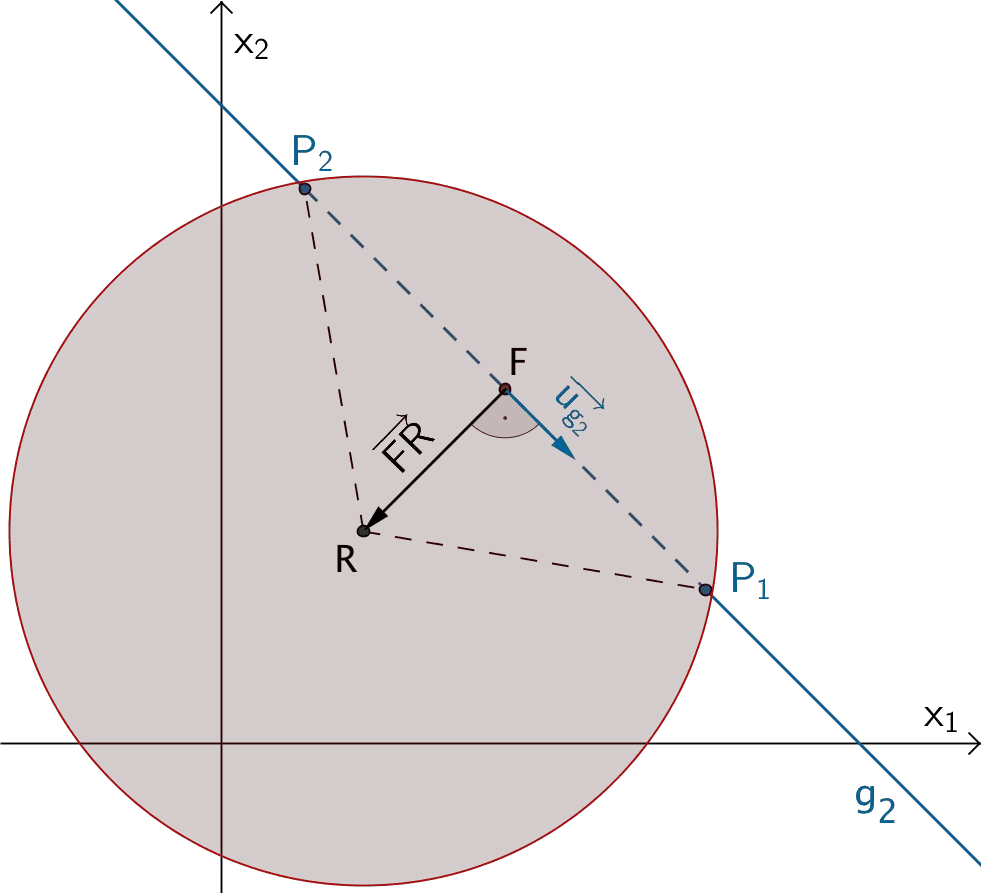
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(P\) auf die Gerade \(g\).
Somit gilt: \(\enspace \overrightarrow{FP} \perp \overrightarrow{u} \quad \Longleftrightarrow \quad \overrightarrow{FP} \circ \overrightarrow{u} = 0\)
1. Verbindungsvektor \(\overrightarrow{FP}\) allgemein beschreiben:
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u \quad \Longrightarrow \quad \overrightarrow{FP} = \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \]
2. Koordinaten des Lotfußpunktes \(F\) bestimmen:
\[\overrightarrow{FP} \circ \overrightarrow{u} = 0 \quad \Longleftrightarrow \quad \left[ \overrightarrow P - \left( \overrightarrow A + \lambda \cdot \overrightarrow u \right) \right] \circ \overrightarrow u = 0\]
\(\Longrightarrow \quad\) Wert für Parameter \(\lambda\)
\[F \in g \colon \overrightarrow F = \overrightarrow A + \lambda \cdot \overrightarrow u\]
3. Länge der Strecke \([FP]\) berechnen:
\[d\,(P;g) = \overline{FP} = \vert \overrightarrow P - \overrightarrow F \vert\]
Es sei \(F\) der Lotfußpunkt des Lotes des Punktes \(R\) auf die Gerade \(g_2\).
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Somit gilt:
\[\overrightarrow{FR} \perp \overrightarrow{u_{g_2}} \enspace \Longleftrightarrow \enspace \overrightarrow{FR} \circ \overrightarrow{u_{g_2}} = 0\]
Vektor \(\overrightarrow{FR}\) allgemein beschreiben:
\[F \in g_2\, \colon \, \overrightarrow F = \begin{pmatrix} 40 + 10\mu \\ 50 - 10\mu \\ 10 \end{pmatrix}\]
\[\begin{align*} \overrightarrow{FR} &= \overrightarrow R - \overrightarrow F \\[0.8em] &= \begin{pmatrix} 20 \\ 30 \\ 0 \end{pmatrix} - \begin{pmatrix} 40 + 10\mu \\ 50 - 10\mu \\ 10 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -20 - 10\mu \\ -20 + 10\mu \\ -10 \end{pmatrix} \end{align*}\]
Koordinaten des Lotfußpunktes \(F\) bestimmen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{FR} \circ \overrightarrow{u_{g_2}} &= 0 \\[0.8em] \begin{pmatrix} -20 - 10\mu \\ -20 + 10\mu \\ -10 \end{pmatrix} \circ \begin{pmatrix} 10 \\ -10 \\ 0 \end{pmatrix} &= 0 \\[0.8em] (-20 -10\mu) \cdot 10 + (-20 + 10\mu) \cdot (-10) + (-10) \cdot 0 &= 0 \\[0.8em] -200 -100\mu +200 -100\mu &= 0 \\[0.8em] -200\mu &= 0 \\[0.8em] \mu &= 0 \end{align*}\]
Parameterwert \(\mu = 0\) in die Geradengleichung von \(g_2\) einsetzen:
\[F \in g_2 \colon \enspace \overrightarrow F = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} + 0 \cdot \begin {pmatrix} 10 \\ -10 \\ 0 \end {pmatrix} = \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} \]
Länge der Strecke \([RF]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[ \begin {align*} \overline{RF} &= \vert \overrightarrow F - \overrightarrow R \vert \\[0.8em] &= \left| \begin {pmatrix} 40 \\ 50 \\ 10 \end {pmatrix} - \begin {pmatrix} 20 \\ 30 \\ 0 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 20 \\ 20 \\ 10 \end {pmatrix} \right| \\[0.8em] &= \sqrt{20^2 + 20^2 + 10^2} \\[0.8em] &= \sqrt{900} \\[0.8em] &= 30 \end {align*} \]
\[\Longrightarrow \quad d(R;g_2) = 30\]
Länge der Strecke \([P_1P_2]\) berechnen:
![Berechnung der Länge der Strecke [P₁P₂] mithilfe des Satzes des Pythagoras Berechnung der Länge der Strecke [P₁P₂] mithilfe des Satzes des Pythagoras](/images/stories/B2014BA_PT_B_G_1/B2014BA_PT_B_G_1_e_05.png)
Die Länge der Strecke \([P_1P_2]\) lässt sich mithilfe des Satzes des Pythagoras berechnen.
\[\begin{align*} \left( \frac{\overline{P_1P_2}}{2} \right)^2 + \overline{RF}^2 &= r^2 & &| -\overline{RF}^2 \\[0.8em] \frac{\overline{P_1P_2}^2}{4} &= r^2 - \overline{RF}^2 & &| \cdot 4 \\[0.8em] \overline{P_1P_2}^2 &= 4 \left( r^2 - \overline{RF}^2 \right) & &| \; \sqrt{\quad} \\[0.8em] \overline{P_1P_2} &= 2 \sqrt{r^2 - \overline{RF}^2} \\[0.8em] &= 2 \sqrt{50^2 - 30^2} \\[0.8em] &= 80 \end{align*}\]
Die Länge der Flugstrecke von \(F_2\) im Überwachungsbereich des Radars beträgt 80 km.