Im Folgenden wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_c \colon x \mapsto f(x) + c\) mit \(c \in \mathbb R\) betrachtet.
Geben Sie in Abhängigkeit von \(c\) ohne weitere Rechnung die Koordinaten des Hochpunkts des Graphen von \(g_c\) sowie das Verhalten von \(g_c\) für \(x \to + \infty\) an.
(2 BE)
Lösung zu Teilaufgabe 2a
\[g_c(x) = f(x) + c\,; \quad c \in \mathbb R\]
Koordinaten des Hochpunkts von \(G_{g_c}\)
Der Graph einer Scharfunktion der Funktionenschar \(g_c\) entsteht durch Verschiebung des Graphen der Funktion \(f\) um \(c\) in \(y\)-Richtung. Somit wird auch der Hochpunkt \(HoP\, \left( 1|\frac{2}{\sqrt{e}} \right)\) von \(G_f\) um \(c\) in \(y\)-Richtung verschoben.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\(\Longrightarrow \quad\) Hochpunkt von \(G_{g_c}\): \(HoP\,\left( 1|\frac{2}{\sqrt{e}} + c \right)\)
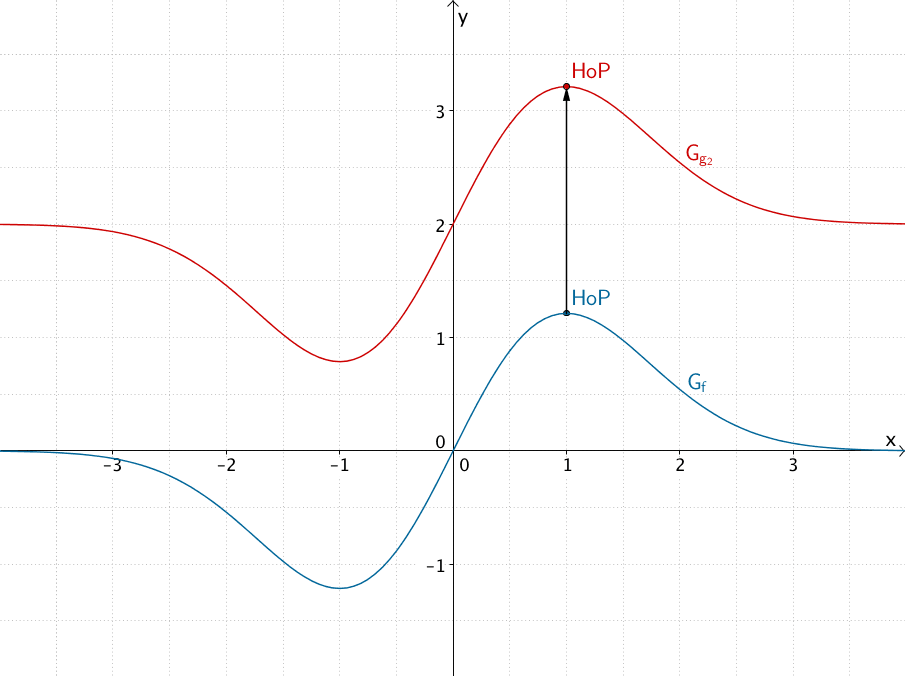
Beispiel, Verschiebung in \(y\)-Richtung um \(c = 2\): \(g_2(x) = f(x) + 2 = 2x \cdot e^{-0{,}5x^2} + 2\)
\(\Longrightarrow \quad\) Hochpunkt von \(G_{g_2}\): \(HoP\,\left(1|\frac{2}{\sqrt{e}} + 2\right)\)
Verhalten von \(g_c\) für \(x \to + \infty\)
Aus Teilaufgabe 1a ist bekannt:
\[\lim \limits_{x \, \to \, + \infty} f(x) = 0\]
Daraus folgt für das Verhalten von \(g_c\) für \(x \to + \infty\):
\[\lim \limits_{x \, \to \, + \infty} g_c(x) = \lim \limits_{x \, \to \, + \infty} (f(x) + c) = c\]
Die Gerade \(y = c\) ist waagrechte Asymptote von \(G_{g_c}\).
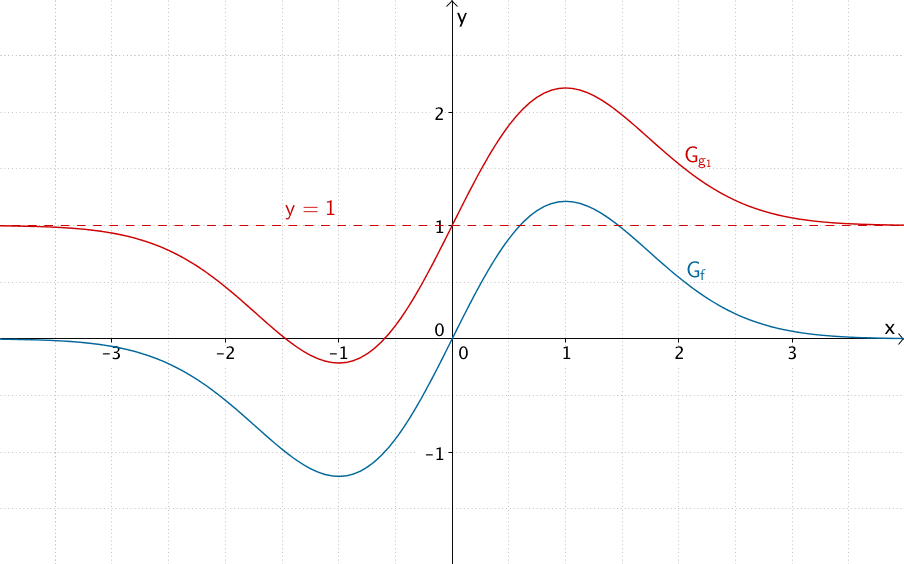
Graph der Scharfunktion \(g_1 = f(x) + 1\) für \(c = 1\) mit waagrechter Asymptote \(y = 1\).

