Mind Map - Gebrochenrationale Funktionen Neu
Definition, Darstellungsformen, Nullstelle(n), Definitionslücken, Polstellen, Asymptoten und Funktionsbestimmungen
![]() Mind Map - Gebrochenrationale Funktionen (HD-PDF mit Wasserzeichen)1.02 MB
Mind Map - Gebrochenrationale Funktionen (HD-PDF mit Wasserzeichen)1.02 MB
![]() Mind Map - Gebrochenrationale Funktionen (komprimiertes PDF ohne Wasserzeichen)471.81 KB
Mind Map - Gebrochenrationale Funktionen (komprimiertes PDF ohne Wasserzeichen)471.81 KB
![]() Einzelne Folien - Gebrochenrationale Funktionen (HD-PDF mit Wasserzeichen)4.18 MB
Einzelne Folien - Gebrochenrationale Funktionen (HD-PDF mit Wasserzeichen)4.18 MB
![]() Einzelne Folien - Gebrochenrationale Funktionen (komprimiertes PDF ohne Wasserzeichen)988.10 KB
Einzelne Folien - Gebrochenrationale Funktionen (komprimiertes PDF ohne Wasserzeichen)988.10 KB
Bei gebrochenrationalen Funktionen können zwei Arten von Grenzwertbetrachtungen unterschieden werden: Das Verhalten in der Nähe der Definitionslücken und das Verhalten im Unendlichen.
Verhalten in der Nähe der Definitionslücken
Die Tabelle gibt eine erste Übersicht. Anschließend wird das Verhalten einer gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) in der Nähe der Definitionslücken erläutert.
| Verhalten in der Nähe einer Definitionslücke \(x = x_{0}, \lim \limits_{x \, \to \, x_{0}} f(x)\) | |||
| Art der Definitionslücke | Beispiel | Vorzeichenwechsel | Asymptote |
|
Polstelle ungerader Ordnung
(einfache, dreifache ... Nennernullstelle)
|
\(f(x) = \dfrac{1}{x - 1}\) |
mit Vorzeichenwechsel
|
Senkrechte Asymptote:
\(x = 1\)
|
|
Polstelle gerader Ordnung
(doppelte, vierfache ... Nennernullstelle)
|
\(f(x) = \dfrac{1}{(x - 1)^{2}}\) |
ohne Vorzeichenwechsel
|
|
|
Hebbare Definitionslücke
(vollständig kürzbare Nennernullstelle)
|
\(f(x) = \dfrac{x - 1}{(x - 1)(x^{2} + 1)}\) | Hebbare Definitionslücke mit Definitionsloch an der Stelle \(x = 1\)
|
|
Verhalten in der Nähe einer Polstelle, senkrechte Asymptoten
Es wird das Verhalten einer gebrochenrationalen Funktion \(f\) bei linksseitiger und rechtsseitiger Annäherung an die Polstelle \(x = x_{0}\) untersucht.
\[\lim \limits_{x \, \to\, x_{0}^{-}} f(x) \qquad \lim \limits_{x \, \to \,x_{0}^{+}} f(x)\]
An einer Polstelle besitzt der Graph einer gebrochenrationalen Funktion eine senkrechte Asymptote mit der Gleichung \(\boldsymbol{x = x_{0}}\). In der Nähe einer Polstelle werden die Funktionswerte einer gebrochenrationalen Funktion beliebig klein bzw. beliebig groß. Das heißt, der Graph einer gebrochenrationalen Funktion verläuft asymptotisch gegen \(-\infty\) bzw. \(+ \infty\). Bei einer Polstelle mit Vorzeichenwechsel (Nennernullstelle ungerader Ordnung) führt die beidseitige Annäherung des Graphen an die senkrechte Asymptote in entgegengesetzte Richtung. Bei einer Polstelle ohne Vorzeichenwechsel (Nennernullstelle gerader Ordnung) führt die beidseitige Annäherung des Graphen an die senkrechte Asymptote in die gleiche Richtung (vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Vielfachheit von Nullstellen).
Senkrechte Asymptote: \(x = x_{0}\)
1. Beispiel:
\[f(x) = \frac{1}{x - 1}\,; \enspace D_{f} = \mathbb R \backslash \{1\}\]
Es liegt die Polstelle \(x = 1\) mit Vorzeichenwechsel vor, da die Nennernullstelle \(x = 1\) von ungerader Ordnung ist (einfache Nennernullstelle).
Gleichung der senkrechten Asymptote: \(x = 1\)
Linksseitige Annäherung, \(x \to 1^{-}\):
\[\lim \limits_{x \, \to \, 1^{-}} f(x) = \lim \limits_{x \, \to \, 1^{-}} \frac{1}{\underbrace{x - 1}_{\to \, 0^{-}}} = -\infty\]
Rechtsseitige Annäherung, \(x \to 1^{+}\):
\[\lim \limits_{x \, \to \, 1^{+}} f(x) = \lim \limits_{x \, \to \, 1^{+}} \frac{1}{\underbrace{x - 1}_{\to \, 0^{+}}} = +\infty\]
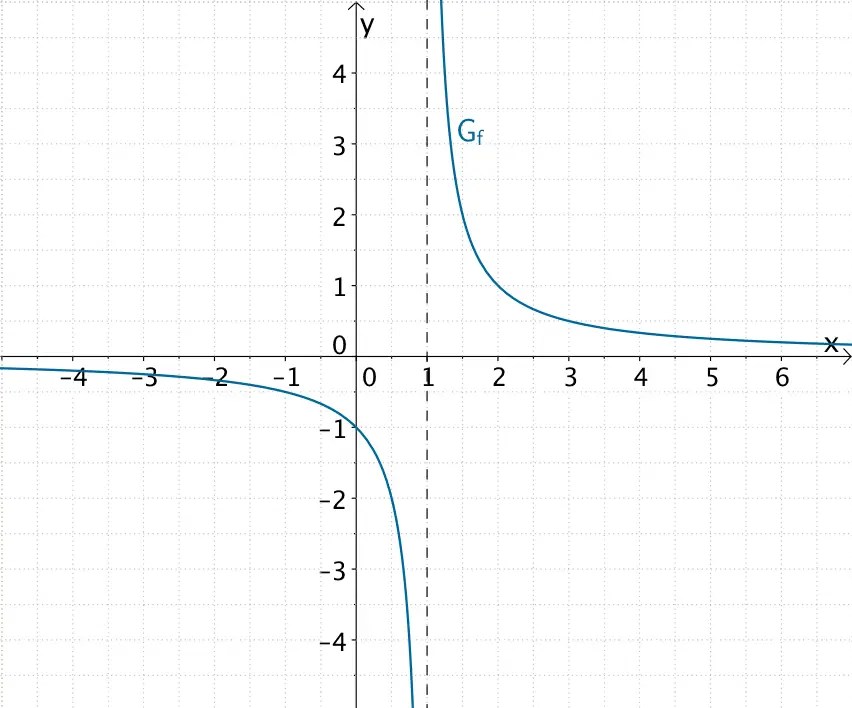
Der Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{1}{x - 1}\) verläuft in der Nähe der Polstelle \(x = 1\) (einfache Nennernullstelle) mit Vorzeichenwechsel.
2. Beispiel:
\[g(x) = \frac{1}{(x - 1)^{2}}\,; \enspace D_{g} = \mathbb R \backslash \{1\}\]
Es liegt die Polstelle \(x = 1\) ohne Vorzeichenwechsel vor, da die Nennernullstelle \(x = 1\) von gerader Ordnung ist (doppelte Nennernullstelle).
Gleichung der senkrechten Asymptote: \(x = 1\)
Linksseitige Annäherung, \(x \to 1^{-}\):
\[\lim \limits_{x \, \to \, 1^{-}} g(x) = \lim \limits_{x \, \to \, 1^{-}} \frac{1}{\underbrace{(x - 1)^{2}}_{\to \, 0^{+}}} = +\infty\]
Rechtsseitige Annäherung, \(x \to 1^{+}\):
\[\lim \limits_{x \, \to \, 1^{+}} g(x) = \lim \limits_{x \, \to \, 1^{+}} \frac{1}{\underbrace{(x - 1)^{2}}_{\to \, 0^{+}}} = +\infty\]
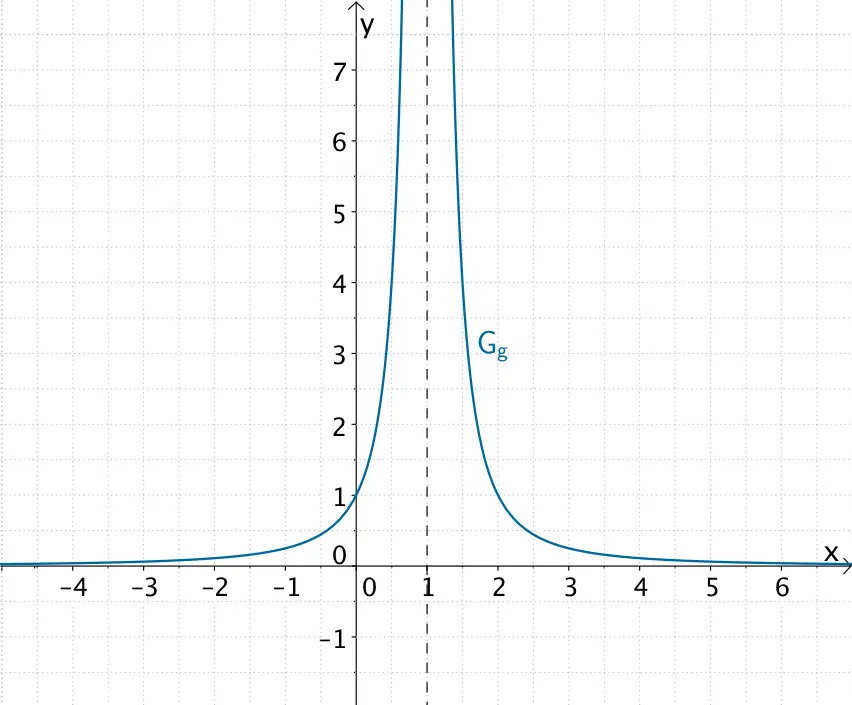
Der Graph der gebrochenrationalen Funktion \(g \colon x \mapsto \dfrac{1}{(x - 1)^{2}}\) verläuft in der Nähe der Polstelle \(x = 1\) (doppelte Nennernullstelle) ohne Vorzeichenwechsel.
Verhalten in der Nähe eines Definitionslochs
Besitzt eine gebrochenrationale Funktion \(f\) an der Stelle \(x = x_{0}\) eine hebbare Definitionslücke (Nennernullstelle ist zugleich Zählernullstelle und vollständig kürzbar), zeigt der Graph von \(f\) an der Stelle \(x = x_{0}\) eine Definitionsloch (vgl.Abiturskript - 1.2.1 Nullstellen und Polstellen).
Das Verhalten einer gebrochenrationalen Funktion in der Nähe einer hebbaren Definitionslücke \(x = x_{0}\) lässt sich durch die Grenzweltbetrachtung \(x \to x_{0}\) am gekürzten Funktionsterm ermitteln.
Beispiel:
\[f(x) = \frac{x - 1}{x^{3} - x^{2} + x - 1}\]
Nennerterm faktorisieren:
\[\begin{align*}f(x) &= \frac{x - 1}{x^{3} - x^{2} + x - 1} & &| \; \text{Durch Probieren:} \; x = 1 \; \text{ist Nennernullstelle} \\[0.8em] &= \frac{\cancel{x - 1}}{\cancel{(x - 1)}(x^{2} + 1)} & &| \; \text{Linearfaktor}\;x - 1\;\text{für}\;x \neq 1\,\text{kürzen} \\[0.8em] &= \frac{1}{x^{2} + 1} \end{align*}\]
Die gebrochenrationale Funktion \(f\) besitzt an der Stelle \(x = 1\) eine hebbare Definitionslücke.
\[\Longrightarrow \quad D_{f} = \mathbb R \backslash \{1\}\]
Verhalten von \(f\) in der Nähe der hebbaren Definitionslücke \(x = 1\):
\[\lim \limits_{x \, \to \, 1} f(x) = \lim \limits_{x \, \to \, 1} \frac{1}{x^{2} + 1} = \frac{1}{2}\]
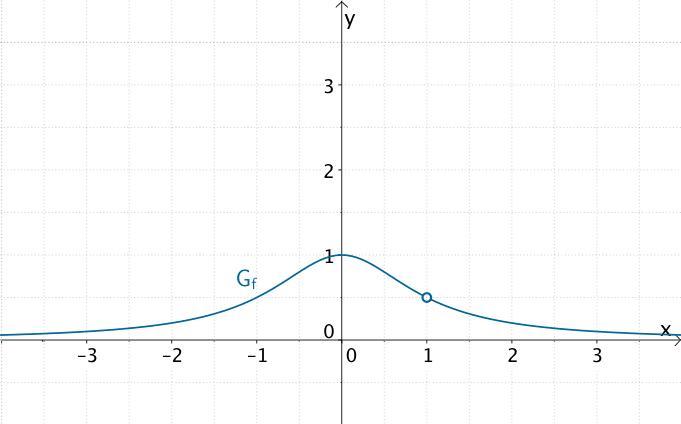
In der Nähe der hebbaren Definitionslücke \(x = 1\) nähert sich der Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{x - 1}{(x - 1)(x^{2} + 1)}\) beliebig nahe dem Wert \(\frac{1}{2}\) an. Der Graph von \(f\) zeigt an der Stelle \(x = 1\) ein Definitionsloch.
Verhalten im Unendlichen, waagrechte und schräge Asymptoten
Die Tabelle gibt eine erste Übersicht. Anschließend wird das Verhalten einer gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) im Unendlichen erläutert.
| Verhalten im Unendlichen, \(\lim \limits_{x \, \to \, \pm \infty}f(x)\) | ||
| Zählergrad / Nennergrad | Beispiel | Asymptote |
| \(m < n\) |
\(f(x) = \dfrac{2x + 2}{4x^{2} + 4x - 24}\)
|
\(x\)-Achse
|
| \(m = n\) |
\(f(x) = \dfrac{2x^{2}+2x}{4x^{2}+4x-24}\)
|
waagrechte Asymptote parallel zur \(x\)-Achse
|
| \(m = n+1\) |
\(f(x) = \dfrac{2x^{3} + 2x^{2}}{4x^{2} + 4x - 24}\)
|
schräge Asymptote
|
| \(m > n+1\) |
\(f(x) = \dfrac{2x^{4} + 2x^{3}}{8x^{2} + 4x - 24}\)
|
keine waagrechte oder schräge Asymptote
|
Der Graph einer gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) zeigt für \(x \to -\infty\) bzw. \(x \to +\infty\) abhängig vom Grad des Zähler- bzw. Nennerpolynoms ein unterschiedliches asymptotisches Verhalten.
\[\lim \limits_{x \, \to \, \pm \infty} f(x) = \lim \limits_{x \, \to \, \pm \infty } \frac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\]
Für die Grenzwertbetrachtung \(\lim \limits_{x \, \to \, \pm \infty} f(x)\) einer gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) wird die höchste Potenz \(x^{n}\) des Nennerpolynoms im Nenner und im Zähler ausgeklammert.
\(m < n\): Grad des Zählerpolynoms kleiner als Grad des Nennerpolynoms
Eine gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) mit \(m < n\) heißt echt gebrochenrationale Funktion. In diesem Fall besitzt der Graph der gebrochenrationalen Funktion \(f\) immer die \(\boldsymbol{x}\)-Achse mit der Gleichung \(\boldsymbol{y = 0}\) als waagrechte Asymptote für das Verhalten im Unendlichen.
\(f(x) = \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\)
mit \(\boldsymbol{m < n}\)
\(G_{f}\) hat für \(x \to \pm \infty\) die waagrechte Asymptote \(\boldsymbol{y = 0}\) (\(\boldsymbol{x}\)-Achse).
Beispiel:
\[f(x) = \frac{2x + 2}{4x^{2} + 4x - 24}\]
\(m = 1\), \(n = 2\)
\(\Longrightarrow \quad m < n \quad \Longrightarrow \quad\)Waagrechte Asymptote: \(y = 0\)
Nachweis der waagrechten Asymptote \(y = 0\) durch Grenzwertbetrachtung:
\[\begin{align*} \lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, -\infty} \frac{2x + 2}{4x^{2} + 4x - 24} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{\cancel{x^{2}}\left( \frac{2}{x} + \frac{2}{x^{2}} \right)}{\cancel{x^{2}}\left( 4 + \frac{4}{x} - \frac{24}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{\overbrace{\frac{2}{x}}^{\to \, 0} + \overbrace{\frac{2}{x^{2}}}^{\to \, 0}}{4 + \underbrace{\frac{4}{x}}_{\to \, 0} - \underbrace{\frac{24}{x^{2}}}_{\to \, 0}} \\[0.8em] &= 0 \end{align*}\]
\(\Longrightarrow \quad\) Die \(x\)-Achse mit der Gleichung \(y = 0\) ist waagrechte Asymptote.
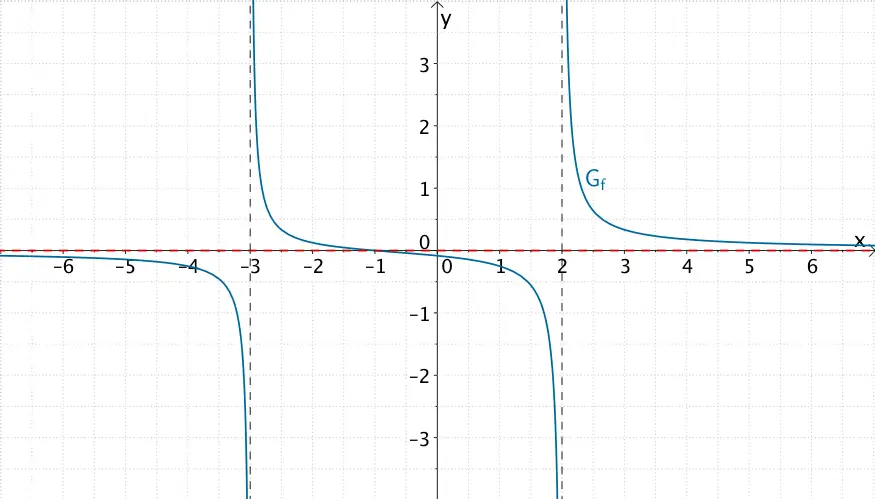
Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{2x + 2}{4x^{2} + 4x - 24}\) mit waagrechter Asymptote \(y = 0\) (\(x\)-Achse)
\(m = n\): Zählerpolynom und Nennerpolynom vom selben Grad
Eine gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) mit \(m = n\) heißt unecht gebrochenrationale Funktion. In diesem Fall besitzt der Graph der gebrochenrationalen Funktion \(f\) eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse für das Verhalten im Unendlichen. Die Gleichung der waagrechten Asymptote ergibt sich aus den Koeffizienten \(a_{m}\) und \(b_{n}\) der höchsten Potenzen des Zähler- bzw. Nennerpolynoms zu: \(y = \dfrac{a_{m}}{b_{n}}\).
\(f(x) = \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\)
mit \(\boldsymbol{m = n}\)
\(G_{f}\) hat für \(x \to \pm \infty\) die waagrechte Asymptote \(\boldsymbol{y = \dfrac{a_{m}}{b_{n}}}\).
Beispiel:
\[f(x) = \frac{2x^{2}+2x}{4x^{2}+4x-24}\]
\(a_{m} = 2\), \(b_{n} = 4\)
\(\Longrightarrow \quad\)Waagrechte Asymptote: \(y = \dfrac{a_{m}}{b_{n}} = \dfrac{2}{4} = \dfrac{1}{2}\)
Nachweis der waagrechten Asymptote \(y = \dfrac{1}{2}\) durch Grenzwertbetrachtung:
\[\begin{align*} \lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} \frac{2x^{2} + 2x}{4x^{2} + 4x - 24} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{\cancel{x^{2}} \left( 2 + \frac{2}{x} \right)}{\cancel{x^{2}} \left( 4 + \frac{4}{x} - \frac{24}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{2 + \overbrace{\frac{2}{x}}^{\to \, 0}}{4 + \underbrace{\frac{4}{x}}_{\to \, 0} - \underbrace{\frac{24}{x^{2}}}_{\to \, 0}} \\[0.8em] &= \frac{2}{4} = \frac{1}{2} \end{align*}\]
\(\Longrightarrow \quad y = \dfrac{1}{2}\) ist waagrechte Asymptote.
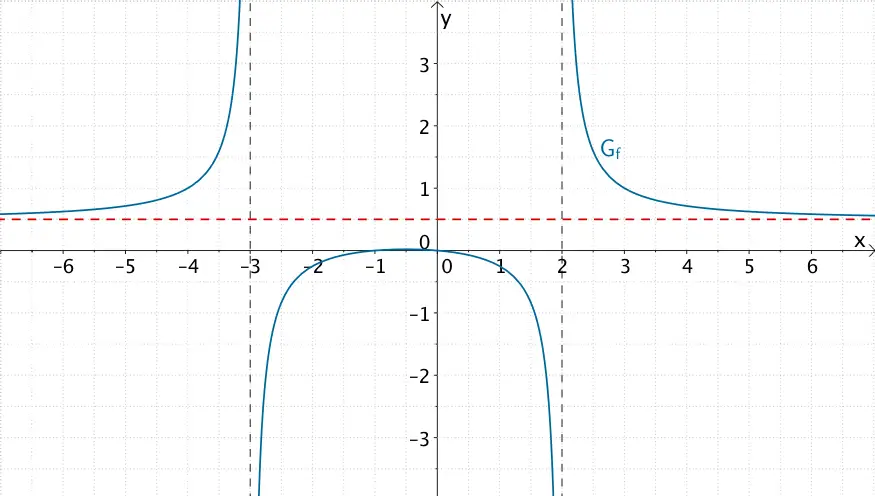
Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{2x^{2}+2x}{4x^{2}+4x-24}\) mit waagrechter Asymptote \(y = \dfrac{1}{2}\)
Der Funktionsterm einer gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) mit \(m = n\) lässt sich durch eine Division des Zählerpolynoms durch das Nennerpolynom (Polynomdivision) in eine Konstante \(c \in \mathbb R\) und einen echt gebrochenrationalen Funktion \(r(x)\) zerlegen.
\[\begin{align*}f(x) &= \frac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}} & &| \; m = n \\[0.8em] &= c + r(x) \end{align*}\]
Ist eine gebrochenrationale Funktion in dieser Form gegeben, so kann die waagrechte Asymptote \(y = c\) direkt entnommen werden, denn es gilt stets \(\lim \limits_{x \to \pm \infty} r(x) = 0\).
\[\lim \limits_{x \, \to \, \pm \infty} f(x) = \lim \limits_{x \, \to \, \pm \infty} c + \underbrace{r(x)}_{\to \, 0} = \lim \limits_{x \, \to \, \pm \infty} c = c\]
Beispiel:
Die bereits betrachtete gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{2x^{2}+2x}{4x^{2}+4x-24}\) kann durch Polynomdivision in die Form \(f(x) = c + r(x)\) zerlegt werden (ohne Nachweis).
\[f(x) = \frac{2x^{2} + 2x}{4x^{2} + 4x - 24} = \frac{1}{2} + \frac{12}{4x^{2} + 4x - 24}\]
Dem Funktionsterm \(f(x) = \dfrac{1}{2} + \dfrac{12}{4x^{2} + 4x - 24}\) kann die waagrechte Asymptote mit der Gleichung \(y = \dfrac{1}{2}\) direkt entnommen werden, denn es gilt: \(\lim \limits_{x \, \to \, \pm \infty} \dfrac{12}{4x^{2} + 4x - 24} = 0\).
Nachweis der waagrechten Asymptote \(y = \dfrac{1}{2}\) durch Grenzwertbetrachtung:
\[\begin{align*}\lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2} + \frac{12}{4x^{2} + 4x - 24} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2} + \frac{\cancel{x^{2}} \cdot \frac{12}{x^{2}}}{\cancel{x^{2}} \left( 4 + \frac{4}{x} - \frac{24}{x^{2}}\right)} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2} + \frac{\overbrace{\frac{12}{x^{2}}}^{\to \, 0}}{ 4 + \underbrace{\frac{4}{x}}_{\to \, 0} - \underbrace{\frac{24}{x^{2}}}_{\to \, 0}} \\[0.8em] &= \frac{1}{2} \end{align*}\]
\(\Longrightarrow \quad y = \dfrac{1}{2}\) ist waagrechte Asymptote.
\(m = n + 1\): Grad des Zählerpolynoms um Eins höher als Grad des Nennerpolynoms
Eine gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) mit \(m = n + 1\) heißt unecht gebrochenrationale Funktion. In diesem Fall besitzt der Graph der gebrochenrationalen Funktion \(f\) eine schräge Asymptote für das Verhalten im Unendlichen.
Eine gebrochenrationale Funktion \(f\) mit \(m = n + 1\) lässt sich durch Division des Zählerpolynoms durch das Nennerpolynom (Polynomdivision) in eine lineare Funktion \(g(x)\) (vgl. Abiturskript - 1.1.1 Lineare Funktion) und eine echt gebrochenrationale Funktion \(r(x)\) zerlegen.
\[\begin{align*}f(x) &= \frac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}} & &| \; m = n + 1 \\[0.8em] &= g(x) + r(x) \end{align*}\]
Ist eine gebrochenrationale Funktion in dieser Form gegeben, so kann die schräge Asymptote \(y = g(x)\) direkt entnommen werden, denn es gilt stets \(\lim \limits_{x \to \pm \infty} r(x) = 0\).
\[\lim \limits_{x \, \to \, \pm \infty} f(x) = \lim \limits_{x \, \to \, \pm \infty} g(x) + \underbrace{r(x)}_{\to \, 0} = \lim \limits_{x \, \to \, \pm \infty} g(x)\]
\(f(x) = \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\)
mit \(\boldsymbol{m = n + 1}\)
\(G_{f}\) hat für \(x \to \pm \infty\) eine schräge Asymptote \(\boldsymbol{y = g(x)}\), wobei g(x) eine lineare Funktion ist.
Beispiel:
\[\begin{align*}f(x) &= \frac{2x^{3} + 2x^{2}}{4x^{2} + 4x - 24} \\[0.8em] &= \frac{1}{2}x + \frac{12x}{4x^{2} + 4x - 24} & &\text{(ohne Nachweis)} \end{align*}\]
\(m = 3\), \(n = 2\)
\(\Longrightarrow \quad m = n + 1 \quad \Longrightarrow \quad\)Schräge Asymptote: \(y = \dfrac{1}{2}x\)
Nachweis der schrägen Asymptote \(y = \dfrac{1}{2}x\) durch Grenzwertbetrachtung:
\[\begin{align*} \lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} \frac{2x^{3} + 2x^{2}}{4x^{2} + 4x - 24} \\[0.8em] & = \lim \limits_{x \, \to \, \pm \infty} x \cdot \frac{2x^{2} + 2x}{4x^{2} + 4x - 24} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} x \cdot \frac{\cancel{x^{2}} \cdot \left( 2 + \frac{2}{x} \right)}{\cancel{x^{2}} \cdot \left( 4 + \frac{4}{x} - \frac{24}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} x \cdot \frac{2 + \overbrace{\frac{2}{x}}^{\to \, 0}}{4 + \underbrace{\frac{4}{x}}_{\to \, 0} - \underbrace{\frac{24}{x^{2}}}_{\to \, 0}} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2}x \\[0.8em] &= \pm \infty \end{align*}\]
bzw.
\[\begin{align*} \lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2}x + \frac{12x}{4x^{2} + 4x - 24} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2}x + \frac{\cancel{x^{2}} \cdot \frac{12}{x}}{\cancel{x^{2}} \left( 4 + \frac{4}{x} - \frac{24}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2}x + \frac{\overbrace{\frac{12}{x}}^{\to \, 0}}{4 + \underbrace{\frac{4}{x}}_{\to \, 0} - \underbrace{\frac{24}{x^{2}}}_{\to \, 0}} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{1}{2}x \\[0.8em] &= \pm \infty \end{align*}\]
Für \(x \to \pm \infty\) nähert sich der Graph der gebrochenrationalen Funktion \(f\) der schrägen Asymptote \(y = \dfrac{1}{2}x\) an und verläuft auf diese Weise gegen \(+\infty\) bzw. \(-\infty\).
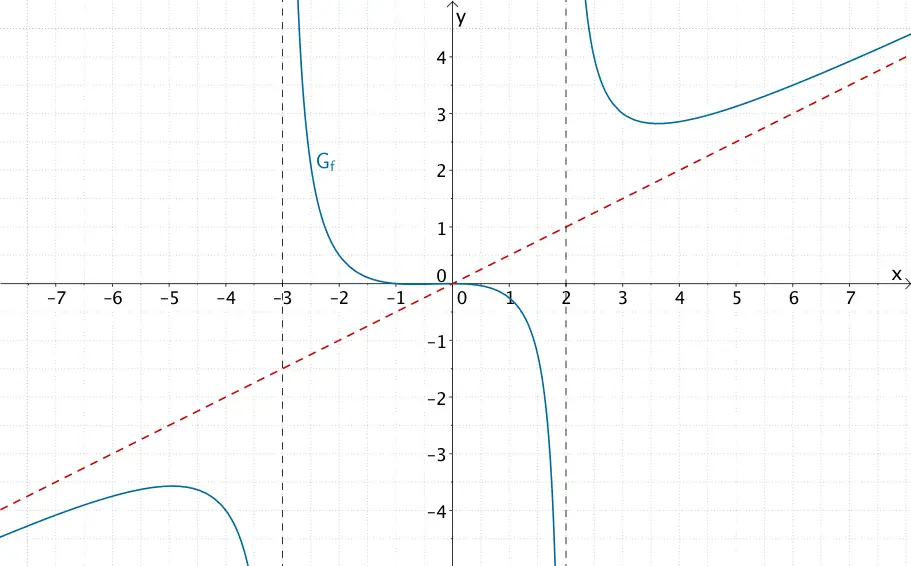
Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{2x^{3} + 2x^{2}}{4x^{2} + 4x - 24}\) mit schräger Asymptote \(y = \dfrac{1}{2}x\)
\(m > n + 1\): Grad des Zählerpolynoms um mehr als Eins höher als Grad des Nennerpolynoms
Eine gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\) mit \(m > n + 1\) ist eine unecht gebrochenrationale Funktion. In diesem Fall besitzt der Graph der gebrochenrationalen Funktion \(f\) keine waagrechte oder schräge Asymptote.
\(f(x) = \dfrac{a_{m}x^{m} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{b_{n}x^{n} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\)
mit \(\boldsymbol{m > n + 1}\)
\(G_{f}\) hat für \(x \to \pm \infty\) keine waagrechte oder schräge Asymptote.
Beispiel:
\[f(x) = \frac{2x^{4} + 2x^{3}}{8x^{2} + 4x - 24}\]
\(m = 4\), \(n = 2\)
\(\Longrightarrow \quad m > n + 1 \quad \Longrightarrow \quad\)Keine waagrechte oder schräge Asymptote
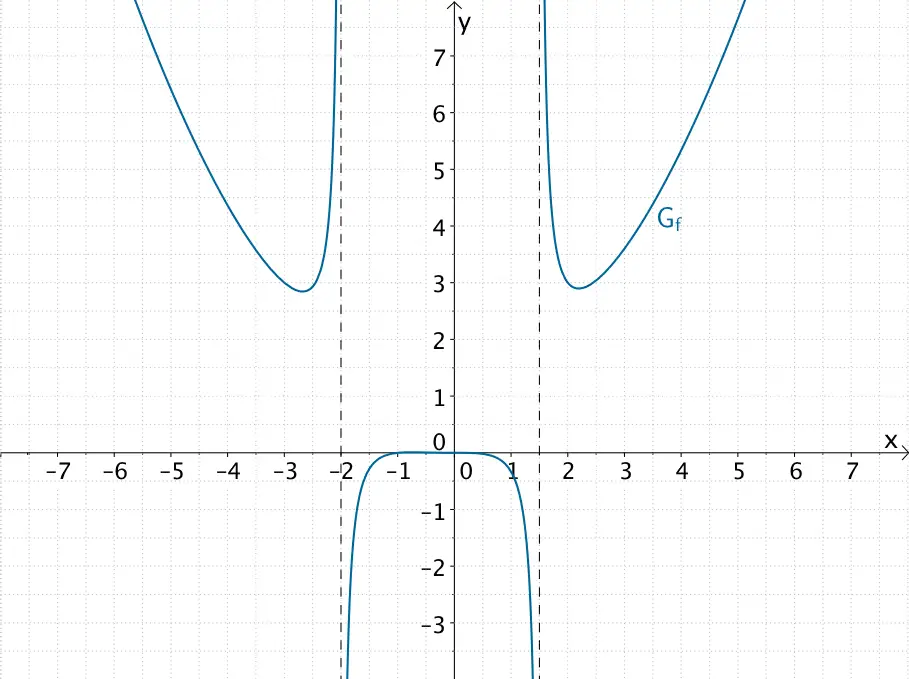
Der Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{2x^{4} + 2x^{3}}{8x^{2} + 4x - 24}\) besitzt keine waagrechte oder schräge Asymptote für das Verhalten im Unendlichen.
Beispielaufgabe
Gegeben sei die gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{2x^{2} - 2}{x^{2} - 4}\). Bestimmen Sie die Nullstellen von \(f\). Ermitteln Sie den maximalen Definitionsbereich von \(f\) und untersuchen Sie das Verhalten an den Definitionsrändern.
\[f(x) = \frac{2x^{2} - 2}{x^{2} - 4}\]
Nullstellen von \(f\):
Für die Bestimmung der Nullstellen werden das Zählerpolynom und das Nennerpolynom zunächst faktorisiert, um ggf. vorhandene gemeinsame Linearfaktoren zu kürzen (mögliche hebbare Definitionslücken).
\[\begin{align*}f(x) &= \frac{2x^{2} - 2}{x^{2} - 4} \\[0.8em] &= \frac{2 \cdot (x^{2} - 1)}{x^{2} - 4} & &| \;\text{3. binomische Formel anwenden} \\[0.8em] &= \frac{2(x - 1)(x + 1)}{(x - 2)(x + 2)} \end{align*}\]
\[f(x) = 0 \quad \Longrightarrow \quad (x - 1)(x + 1) = 0\]
\(\Longrightarrow \quad\)Nullstellen: \(x = -1\) und \(x = 1\)
Maximaler Definitionsbereich von \(f\):
Um mögliche Definitionslücken von \(f\) zu ermitteln, wird das Nennerpolynom auf Nullstellen untersucht.
\[(x - 2)(x + 2) = 0\]
\(\Longrightarrow \quad\)Einfache Nennernullstellen: \(x = -2\) und \(x = 2\)
Die Funktion \(f\) besitzt an der Stelle \(x = -2\) und \(x = 2\) jeweils eine Polstelle mit Vorzeichenwechsel.
\[\Longrightarrow \quad D_{f} = \mathbb R \backslash \{-2;2\}\]
Verhalten an den Polstellen \(x = -2\) und \(x = 2\):
\[\lim \limits_{x \, \to \, -2^{-}} f(x) = \lim \limits_{x \, \to \, -2^{-}} \frac{\overbrace{2x^{2} - 2}^{\to \, 6}}{\underbrace{x^{2} - 4}_{\to \, 0^{+}}} = +\infty\]
\[\lim \limits_{x \, \to \, -2^{+}} f(x) = \lim \limits_{x \, \to \, -2^{+}} \frac{\overbrace{2x^{2} - 2}^{\to \, 6}}{\underbrace{x^{2} - 4}_{\to \, 0^{-}}} = -\infty\]
\[\lim \limits_{x \, \to \, 2^{-}} f(x) = \lim \limits_{x \, \to \, 2^{-}} \frac{\overbrace{2x^{2} - 2}^{\to \, 6}}{\underbrace{x^{2} - 4}_{\to \, 0^{-}}} = -\infty\]
\[\lim \limits_{x \, \to \, 2^{+}} f(x) = \lim \limits_{x \, \to \, 2^{+}} \frac{\overbrace{2x^{2} - 2}^{\to \, 6}}{\underbrace{x^{2} - 4}_{\to \, 0^{+}}} = +\infty\]
Verhalten im Unendlichen, \(x \to \pm \infty\):
\[f(x) = \frac{2x^{2} - 2}{x^{2} - 4}\]
Das Zählerpolynom und das Nennerpolynom der Funktion \(f\) sind vom selben Grad.
Waagrechte Asymptote: \(y = \dfrac{a_{m}}{b_{n}} = \dfrac{2}{1} = 2\)
Nachweis der waagrechten Asymptote \(y = 2\) durch Grenzwertbetrachtung:
\[\begin{align*} \lim \limits_{x \, \to \, \pm \infty} f(x) &= \lim \limits_{x \, \to \, \pm \infty} \frac{2x^{2} - 2}{x^{2} - 4} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{\cancel{x^{2}} \left( 2 - \frac{2}{x^{2}} \right)}{\cancel{x^{2}} \left( 1 - \frac{4}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x \, \to \, \pm \infty} \frac{2 - \overbrace{\frac{2}{x^{2}}}^{\to \, 0}}{1 - \underbrace{\frac{4}{x^{2}}}_{\to \, 0}} \\[0.8em] &= 2 \end{align*}\]
\(\Longrightarrow \quad y = 2\) ist waagrechte Asymptote.
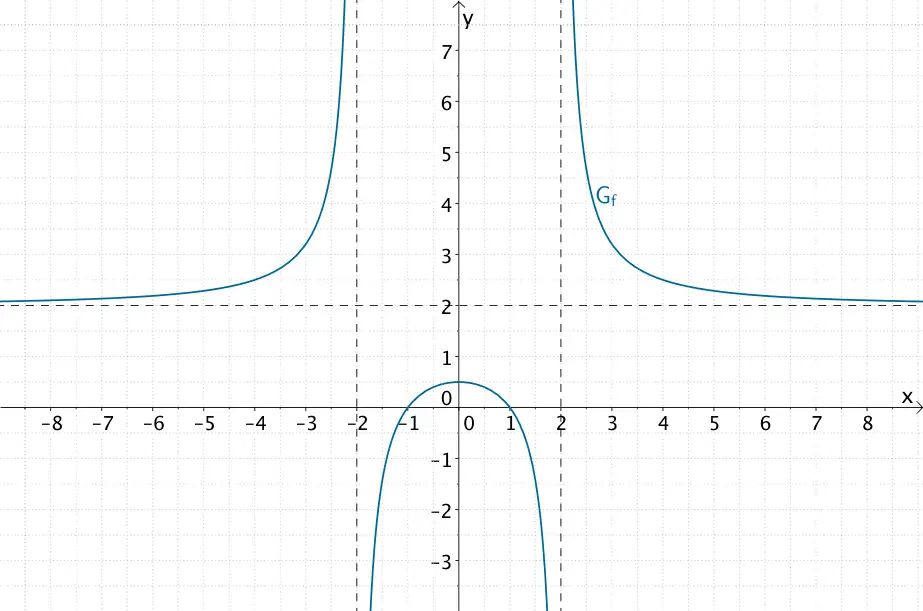
Graph der gebrochenrationalen Funktion \(f \colon x \mapsto \dfrac{2x^{2} - 2}{x^{2} - 4}\)


