Das Baumdiagramm in Abbildung 2 gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen \(A\) und \(B\). Bestimmen Sie die Wahrscheinlichkeit des Ereignisses \(B\).
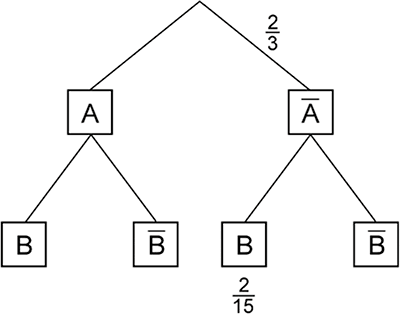Abb. 2
(3 BE)
Lösung zu Teilaufgabe 3
Stochastische Unabhängigkeit
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\[P(A) \cdot P(B) = P(A \cap B)^*\]
gilt.
Bedeutung: Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw. \(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw. \(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\)
gilt.
Nicht verwechseln! Die Unvereinbarkeit zweier Ereignisse \(A\) und \(B\) liegt vor, wenn \(A \cap B = \{\}\).
Allgemeines Baumdiagramm zweier Ereignisse \(A\) und \(B\) mit den bedingten Wahrscheinlichkeiten an den Pfaden der zweiten Stufe
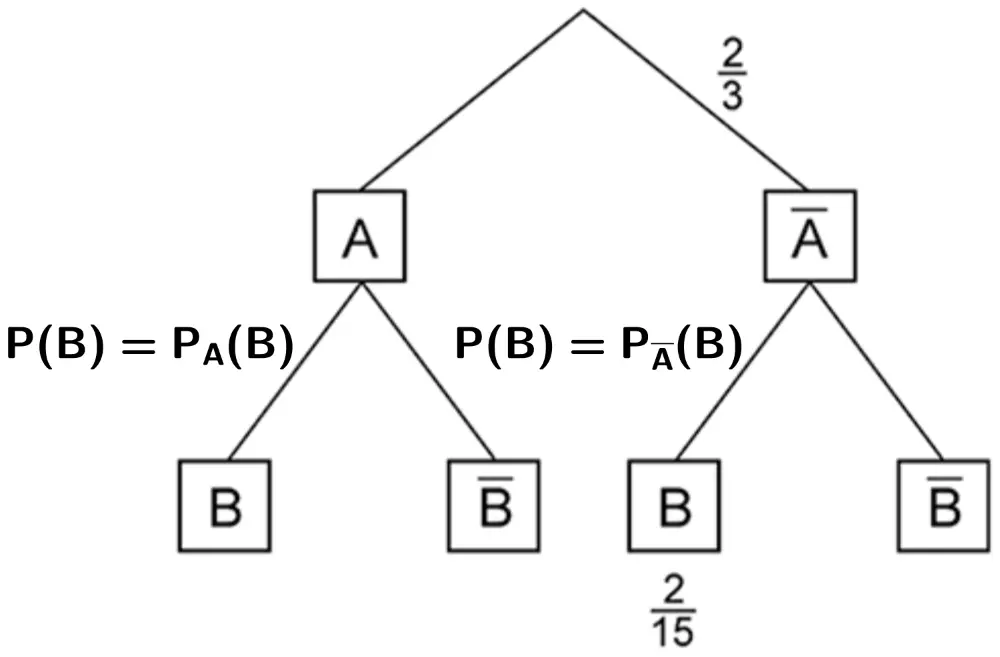
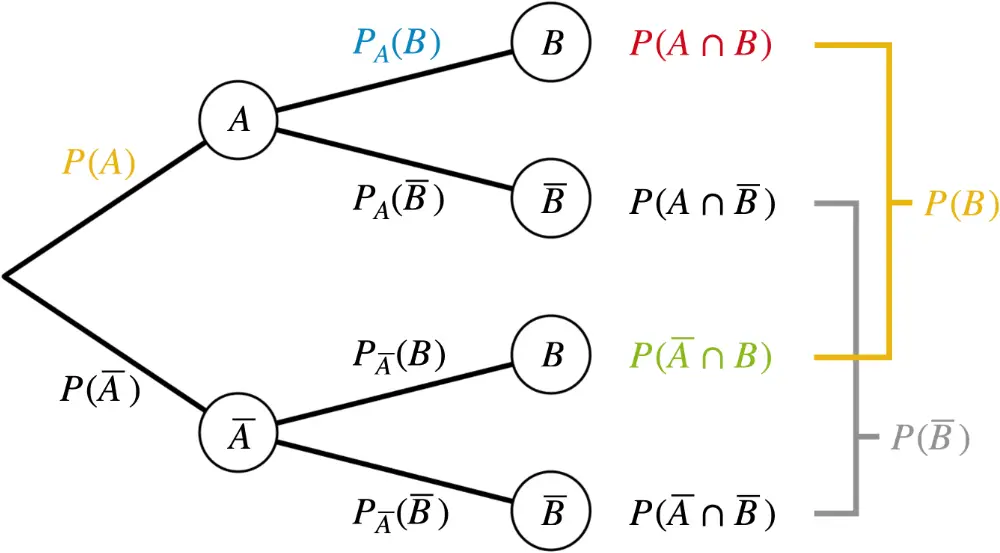
Baumdiagramm von zwei stochastisch unabhängigen Ereignissen \(A\) und \(B\). An den Pfaden der zweiten Stufe sind jeweils die gleichen Wahrscheinlichkeiten \(\textcolor{#89ba17}{P(B)}\) und \(\textcolor{#89ba17}{P(\overline{B})}\) angetragen.
| \(B\) | \(\overline{B}\) | ||
| \(A\) | \(P(A \cap B) = \textcolor{#e9b509}{P(A)} \cdot \textcolor{#0087c1}{P(B)}\) | \(P(A \cap \overline{B}) = \textcolor{#e9b509}{P(A)} \cdot \textcolor{#0087c1}{P(\overline{B})}\) | \(\textcolor{#e9b509}{P(A)}\) |
| \(\overline{A}\) | \(P(\overline{A} \cap B) = \textcolor{#e9b509}{P(\overline{A})} \cdot \textcolor{#0087c1}{P(B)}\) | \(P(\overline{A} \cap \overline{B}) = \textcolor{#e9b509}{P(\overline{A})} \cdot \textcolor{#0087c1}{P(\overline{B})}\) | \(\textcolor{#e9b509}{P(\overline{A})}\) |
| \(\textcolor{#0087c1}{P(B)}\) | \(\textcolor{#0087c1}{P(\overline{B})}\) | \(1\) |
Im Falle zweier unabhängiger Ereignisse \(A\) und \(B\) ist die Vierfeldertafel eine Multiplikationstafel. Die Einträge der inneren Zellen sind das Produkt der zugehörigen Einträge der äußeren Zellen.
Da die Ereignisse \(A\) und \(B\) stochastisch unabhängig sind (vgl. Angabe), gilt:
\(P(B) = P_{A}(B)\) und \(P(B) = P_{\overline{A}}(B)\).
Das heißt, das Ereignis \(B\) tritt unabhängig davon, ob zuvor das Ereignis \(A\) oder \(\overline{A}\) eingetreten ist, mit der gleichen Wahrscheinlichkeit \(P(B)\) ein.
Ein Baumdiagramm ist ein äußerst anschauliches Hilfsmittel für die Berechnung von Wahrscheinlichkeiten bei mehrstufigen Zufallsexperimenten. Jeder Pfad eines Baumdiagramms führt genau zu einem Ergebnis.
Es gelten folgende Pfadregeln:
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines einzelnen Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, deren Pfade zu diesem Ereignis gehören.
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
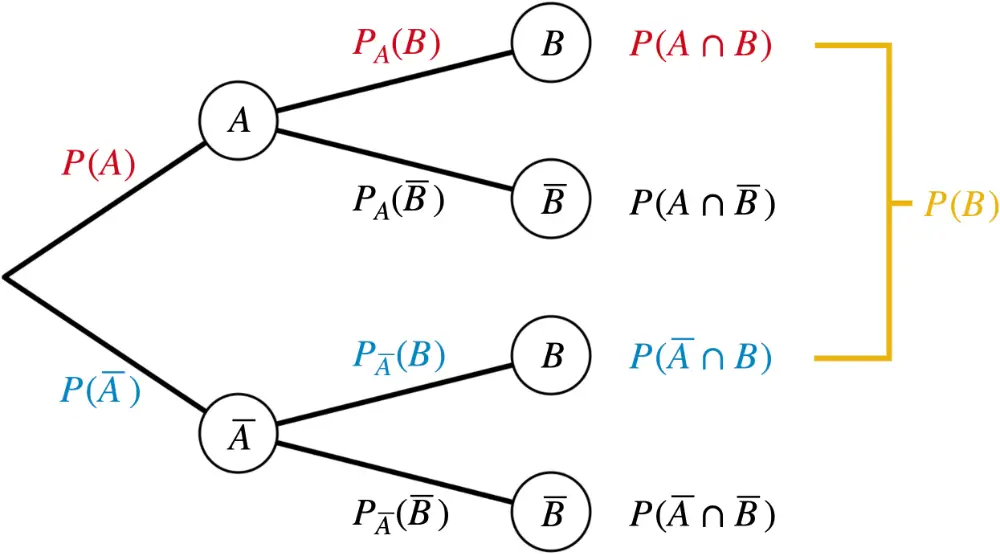
\[\begin{align*} \textcolor{#e9b509}{P(B)} &= \underbrace{\textcolor{#cc071e}{P(A \cap B)} + \textcolor{#0087c1}{P(\overline{A} \cap B)}}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= \underbrace{\textcolor{#cc071e}{P(A)} \cdot \textcolor{#cc071e}{P_A(B)}}_{\large{\text{1. Pfadregel}}} + \underbrace{\textcolor{#0087c1}{P(\overline{A})} \cdot \textcolor{#0087c1}{P_{\overline{A}}(B)}}_{\large{\text{1. Pfadregel}}}\end{align*}\]
Ein Laplace-Würfel mit verschiedenfarbigen Seitenflächen wird zweimal geworfen. Eine Seitenfläche des Würfels ist rot, zwei Seitenflächen sind gelb und drei sind blau.
Bestimmen Sie die Wahrscheinlichkeit für das Ereignis \(E\): „Beide Würfe zeigen die gleiche Farbe."
\(P(\text{„}\textcolor{#cc071e}{\text{rot}}\text{"}) = \textcolor{#cc071e}{\dfrac{1}{6}}\), \(P(\text{„}\textcolor{#e9b509}{\text{gelb}}\text{"}) = \textcolor{#e9b509}{\dfrac{1}{3}}\), \(P(\text{„}\textcolor{#0087c1}{\text{blau}}\text{"}) = \textcolor{#0087c1}{\dfrac{1}{2}}\)
\[E = \{(\textcolor{#cc071e}{rr}),(\textcolor{#e9b509}{gg}),(\textcolor{#0087c1}{bb})\}\]
\[\begin{align*}P(E) &= \underbrace{P(\textcolor{#cc071e}{rr})+P(\textcolor{#e9b509}{gg})+P(\textcolor{#0087c1}{bb})}_{\large{\text{2. Pfadregel}}}\\ &= \underset{\large{\text{jeweils 1. Pfadregel}}}{\underbrace{\textcolor{#cc071e}{\frac{1}{6}} \cdot \textcolor{#cc071e}{\frac{1}{6}}} + \underbrace{\textcolor{#e9b509}{\frac{1}{3}} \cdot \textcolor{#e9b509}{\frac{1}{3}}} + \underbrace{\textcolor{#0087c1}{\frac{1}{2}} \cdot \textcolor{#0087c1}{\frac{1}{2}}}} \\[0.8em] &= \textcolor{#cc071e}{\frac{1}{36}} + \textcolor{#e9b509}{\frac{1}{9}} + \textcolor{#0087c1}{\frac{1}{4}} = \frac{1}{36} + \frac{4}{36} + \frac{9}{36} \\[0.8em] &= \frac{14}{36} = \frac{7}{18} \end{align*}\]
Somit folgt nach der 1. Pfadregel bzw. mithilfe der Formel für die bedingte Wahrscheinlichkeit:
Bei der Betrachtung eines zweistufigen Zufallsexperiments mit den Ereignissen \(A\) und \(B\) müssen zwei Fälle sorgfältig unterschieden werden.
1. Die Ereignisse \(A\) und \(B\) treten zugleich ein (\(A \cap B\)).
2. Das Ereignis \(B\) tritt unter der Bedingung ein, dass das Ereignis \(A\) bereits eingetreten ist.
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_A(B)\) gekennzeichnet.
Es gilt: \(P_A(B) = \dfrac{P(A \cap B)}{P(A)} \enspace (P(A) \neq 0)\)
Die bedingten Wahrscheinlichkeiten werden bei einem Baumdiagramm an den Pfaden der zweiten Stufe (und ggf. höher) angetragen.
An den Enden der Pfade stehen die Wahrscheinlichkeiten für das gleichzeitige Eintreten der Ereignisse.
Nach der 1. Pfadregel (Multiplikationsregel) gilt beispielsweise:
\[\begin{align*}\textcolor{#e9b509}{P(A)} \cdot \textcolor{#0087c1}{P_A(B)} &= \textcolor{#cc071e}{P(A \cap B)} \\[0.8em] \Leftrightarrow \textcolor{#0087c1}{P_A(B)} &= \dfrac{\textcolor{#cc071e}{P(A \cap B)}}{\textcolor{#e9b509}{P(A)}}\end{align*}\]
Analog gilt für ein Baumdiagramm, das mit den Ereignissen \(B\) und \(\overline{B}\) beginnt, mithilfe der 1. und 2. Pfadregel:
\[\begin{align*}\textcolor{#e9b509}{P(B)} \cdot \textcolor{#0087c1}{P_B(A)} &= \textcolor{#cc071e}{P(A \cap B)} \\ \Leftrightarrow \textcolor{#0087c1}{P_B(A)} &= \frac{\textcolor{#cc071e}{P(A \cap B)}}{\textcolor{#e9b509}{P(B)}} \\\textcolor{#0087c1}{P_B(A)} &= \frac{\textcolor{#cc071e}{P(A \cap B)}}{\textcolor{#cc071e}{P(A \cap B)}+ \textcolor{#89ba17}{P(\overline{A} \cap B)}}\end{align*}\]
| \(B\) | \(\overline{B}\) | ||
| \(A\) | \(\textcolor{#cc071e}{P(A \cap B)}\) | \(P(A \cap \overline{B})\) | \(\textcolor{#e9b509}{P(A)}\) |
| \(\overline{A}\) | \(P(\overline{A} \cap B)\) | \(P(\overline{A} \cap \overline{B})\) | \(P(\overline{A})\) |
| \(\textcolor{#e9b509}{P(B)}\) | \(P(\overline{B})\) | \(1\) |
\[\textcolor{#0087c1}{P_A(B)} = \frac{\textcolor{#cc071e}{P(A \cap B)}}{\textcolor{#e9b509}{P(A)}} \qquad \textcolor{#0087c1}{P_B(A)} = \frac{\textcolor{#cc071e}{P(A \cap B)}}{\textcolor{#e9b509}{P(B)}}\]
Die bedingten Wahrscheinlichkeiten ergeben sich bei einer Vierfeldertafel als Quotient aus dem Eintrag einer inneren Zelle und dem Eintrag einer Randzelle.
\[\begin{align*}P(\overline{A}) \cdot P_{\overline{A}}(B) = P(\overline{A} \cap B) \Leftrightarrow P_{\overline{A}}(B) &= \frac{P(\overline{A} \cap B)}{P(\overline{A})} \\[0.8em] P(B) &= \frac{P(\overline{A} \cap B)}{P(\overline{A})} \\[0.8em] &= \frac{\frac{2}{15}}{\frac{2}{3}} \\[0.8em] &= \frac{\cancel{2}}{15} \cdot \frac{3}{\cancel{2}} \\[0.8em] &= \frac{1}{5} \end{align*}\]
