Die \(x_{1}x_{2}\)-Ebene beschreibt modellhaft eine horizontale Fläche, auf der eine Achterbahn errichtet wurde. Ein gerader Abschnitt der Bahn beginnt im Modell im Punkt \(A\) und verläuft entlang der Geraden \(g\). Der Vektor \(\displaystyle \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\) beschreibt die Fahrtrichtung auf diesem Abschnitt.
Berechnen Sie im Modell die Größe des Winkels, unter dem dieser Abschnitt der Achterbahn gegenüber der Horizontalen ansteigt.
(3 BE)
Lösung zu Teilaufgabe b
Schnittwinkel zwischen Gerade und Ebene
\[g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\,; \enspace \lambda \in \mathbb R\]
\[\overrightarrow{v} = \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
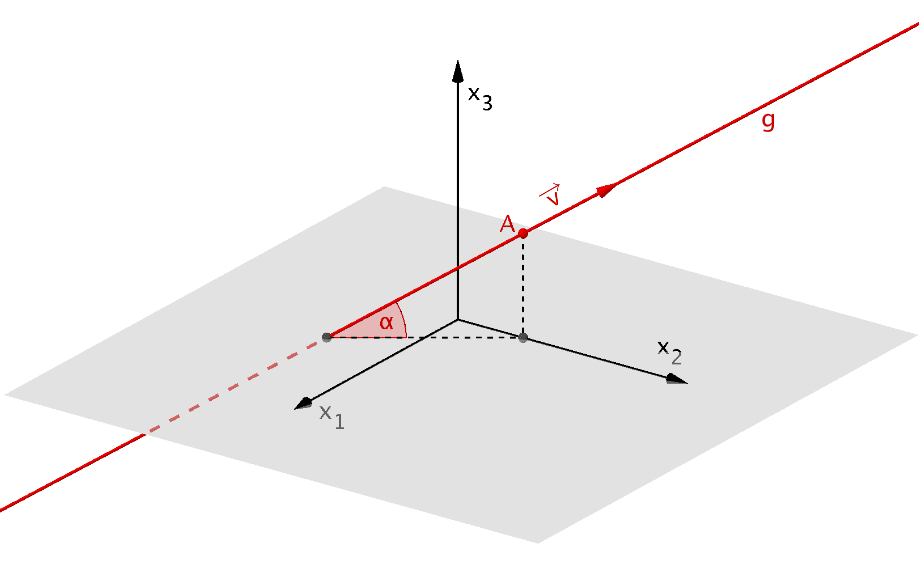
Schnittwinkel \(\alpha\) zwischen der Geraden \(g\) und der \(x_{1}x_{2}\)-Ebene.
Schnittwinkel \(\boldsymbol{\varphi}\) zwischen Gerade und Ebene
\[\cos{(90^{\circ} - \varphi)} = \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert}\]
Mit \(\cos{(90^{\circ}-\varphi)} = \sin{\varphi}\) folgt:
\[\begin{align*}\sin{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \sin^{-1}(\cdots)\end{align*}\]
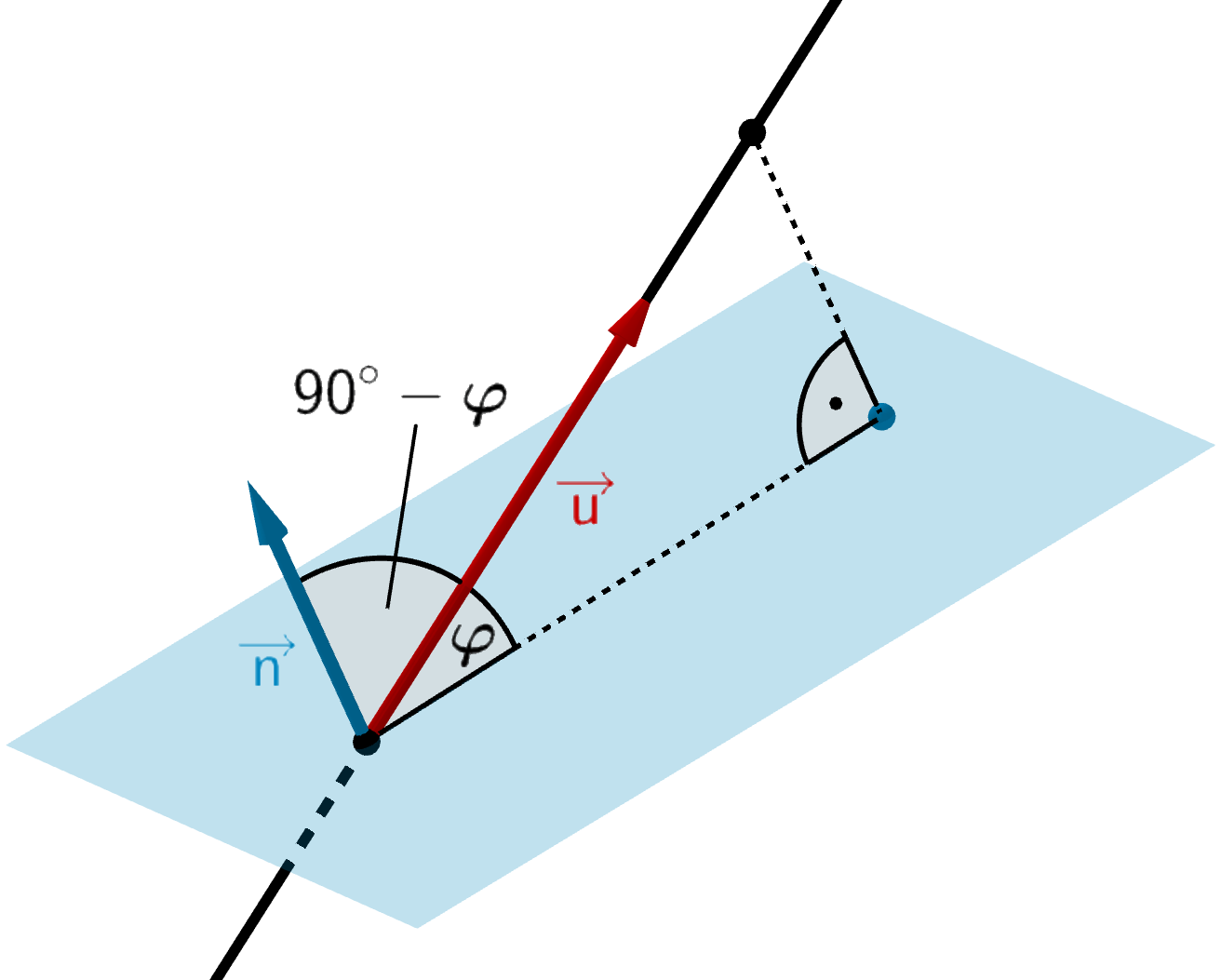
Normalenvektor der \(x_{1}x_{2}\)-Ebene:
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
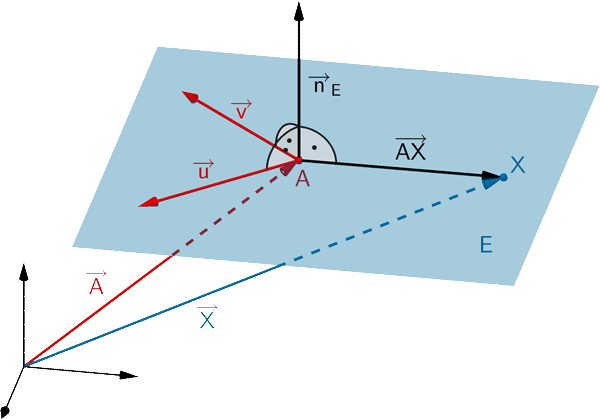
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[x_{1}x_{2}\text{-Ebene}\colon x_{3} = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
Richtungsvektor der Geraden \(g\):
\[\overrightarrow{v} = \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\]
Schnittwinkel \(\alpha\) berechnen:
\[\begin{align*} \sin{\alpha} &= \frac{\vert \overrightarrow{v} \circ \overrightarrow{n}_{x_{1}x_{2}} \vert}{\vert \overrightarrow{v} \vert \cdot \vert \overrightarrow{n}_{x_{1}x_{2}} \vert} \\[0.8em] &= \frac{\left| \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert (-1) \cdot 0 + \sqrt{2} \cdot 0 + 1 \cdot 1 \vert}{\sqrt{(-1)^{2} + (\sqrt{2})^{2} + 1^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{1}{\sqrt{4} \cdot \sqrt{1}} \\[0.8em] &= \frac{1}{2} \\[3.2em] \alpha &= 30^{\circ} \end{align*}\]


