Zu Beginn eines Ausatemvorgangs befinden sich 3,5 Liter Luft in der Lunge der Testperson. Skizzieren Sie auf der Grundlage des Modells unter Berücksichtigung des Ergebnisses aus Aufgabe 3c in einem Koordinatensystem für \(0 \leq t \leq 8\) den Graphen einer Funktion, die den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt.
(3 BE)
Lösung zu Teilaufgabe 3d
Funktionsgraphen im Sachzusammenhang skizzieren
\[g(t) = -\frac{\pi}{8} \sin \left( \frac{\pi}{2}t \right)\,; \enspace D = \mathbb R_{0}^{+}\]
Ergebnis aus Teilaufgabe 3c:
\[\int_{2}^{4} g(t)\,dt = 0{,}5\]
In der Zeit von der zweiten bis zur vierten Sekunde seit Beobachtungsbeginn atmet die Testperson 0,5 Liter Luft ein.
Auf der Grundlage des Modells bedeutet das Ergebnis aus Teilaufgabe 3c, dass das Luftvolumen in der Lunge der Testperson beim Einatmen um 0,5 Liter zunimmt und beim Ausatmen um 0,5 Liter abnimmt. Da sich zu Beginn eines Ausatemvorgangs 3,5 Liter Luft in der Lunge der Testperson befinden, beträgt das Luftvolumen zu Beginn eines Einatemvorgangs somit 3,0 Liter.
Zu Begin eines Ausatemvorgangs ist das Luftvolumen in der Lunge der Testperson also mit 3,5 Liter maximal und zu Beginn eines Einatemvorgangs ist das Luftvolumen mit 3,0 Liter minimal.
Ein Einatemvorgang sowie ein Ausatemvorgang dauert jeweils zwei Sekunden lang.
Im betrachteten Zeitraum \(t \in [0;8]\) (t in Sekunden) ist das Luftvolumen in der Lunge der Testperson
für \(t = 0\), \(t= 4\) bzw. \(t = 8\) mit 3,5 Liter maximal und
für \(t = 2\) bzw. \(t = 6\) mit 3,0 Liter minimal.
Aus Teilaufgabe 3c ist weiterhin bekannt, dass die Stammfunktionen \(G\) der Funktion \(g\) Kosinusfunktionen sind: \(\displaystyle G(t) = \frac{1}{4}\cos\left( \frac{\pi}{2}t \right) + C\).
Die Funktion, die den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt, ist eine Integralfunktion über die Funktion \(g\), welche die Atemstromstärke (momentane Änderungsrate des Luftvolumens) beschreibt.
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung ist jede Integralfunktion über die Funktion \(g\) eine Stammfunktion \(G\) von \(g\). Folglich ist der Graph der Funktion, die den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt, der Graph einer Kosinusfunktion mit dem Wertebereich \(W = [3{,}0;3{,}5]\). Das heißt, der Graph oszilliert mit der Amplitude \(\vert 0{,}25 \vert\) um die Gerade \(y = 3{,}25\) (siehe Ergänzung: Bestimmung des Funktionsterms).
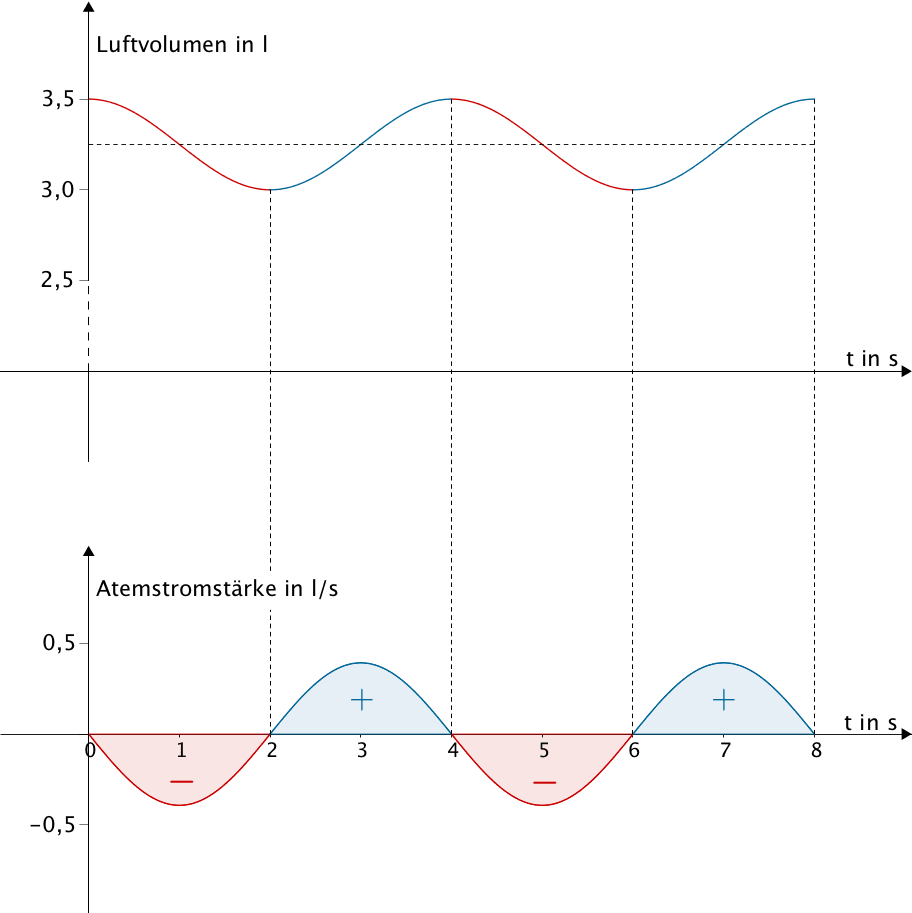
Zeitlicher Verlauf der Atemstromstärke, welche durch die Funktion \(g\) beschrieben wird und zeitlicher Verlauf des Luftvolumens in der Lunge der Testperson, welches durch eine Integralfunktion über die Funktion \(g\) beschrieben wird.
Ergänzung: Betrachtung der Extrempunkte der Funktion \(g\)
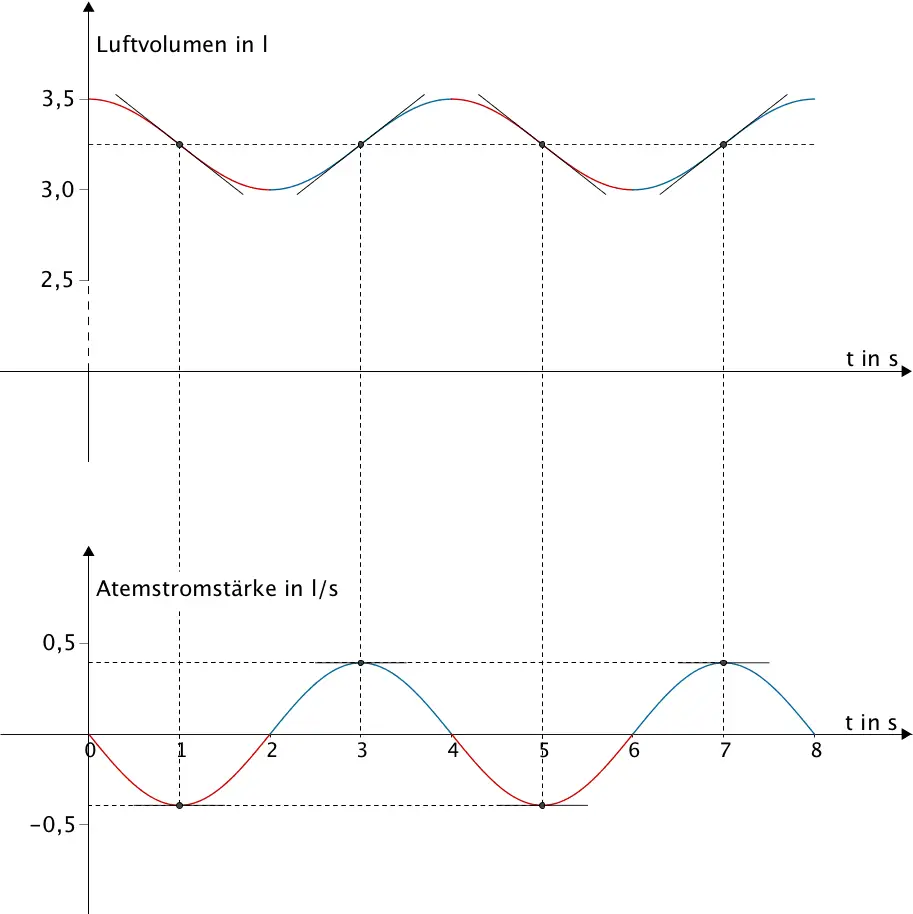
Extrempunkte der Funktion \(g\), deren Graph den zeitlichen Verlauf der Atemstromstärke beschreibt und Wendepunkte mit Wendetangenten der Integralfunktion über \(g\), deren Graph den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt.
Im Folgenden sei \(V\) die Integralfunktion, welche den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt und \(G_{V}\) der Graph dieser Integralfunktion.
An den Extremstellen \(t = 1\), \(t = 3\), \(t = 5\) und \(t = 7\) hat der Graph der Funktion \(g\) waagrechte Tangenten. Die erste Ableitung \(g'\) der Funktion \(g\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(g\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[\Longrightarrow \quad g'(1) = 0\,; \enspace g'(3) = 0\,; \enspace g'(5) = 0\,; \enspace g'(7) = 0\]
Nach dem Hauptsatz der Differential- und Integralrechnung folgt daraus:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[g'(1) = V''(1) = 0\]
\[g'(3) = V''(3) = 0\]
\[g'(5) = V''(5) = 0\]
\[g'(7) = V''(7) = 0\]
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
In der Umgebung der Extremstellen ändert der Graph der Funktion \(g\) (Atemstromstärke) das Monotonieverhalten, d.h. \(g' = V''\) wechselt das Vorzeichen. Demnach sind die Extremstellen des Graphen der Funktion \(g\) die Wendestellen des Graphen der Integralfunktion \(V\).
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\(\Longrightarrow \quad\)\(W_{1}\,(1|V(1))\), \(W_{2}\,(3|V(3))\), \(W_{3}\,(5|V(5))\) und \(W_{4}\,(7|V(7))\) sind für \(t \in [0;8]\) (t in Sekunden) Wendepunkte des Graphen der Integralfunktion \(V\).
Wendetangenten \(w\) von \(G_{V}\):
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Die Steigungen der Wendetangenten in den Wendepunkten der Integralfunktion \(V\) lassen sich am Graphen der Funktion \(g\) (Atemstromstärke) und unter Berücksichtigung des Hauptsatzes der Differential- Und Integralrechnung direkt ablesen:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[g(1) = V'(1) = m_{w_{1}} \approx -0{,}4\]
\[g(3) = V'(3) = m_{w_{2}} \approx 0{,}4\]
\[g(5) = V'(5) = m_{w_{3}} \approx -0{,}4\]
\[g(7) = V'(7) = m_{w_{4}} \approx 0{,}4\]
{zen-exclamation-circle}Wichtig:{/zen-exclamation-circle} Die Extremstellen des Graphen der Ableitung \(f'\) einer Funktion \(f\) sind immer die Wendestellen des Graphen einer Funktion \(f\). An den Wendestellen ist die Steigung des Graphen einer Funktion \(f\) (Steigung der Wendetangente) maximal oder minimal. Das Krümmungsverhalten des Graphen einer Funktion \(f\) ändert sich an den Wendestellen.
Graphenkrümmung des Graphen der Integralfunktion \(V\):
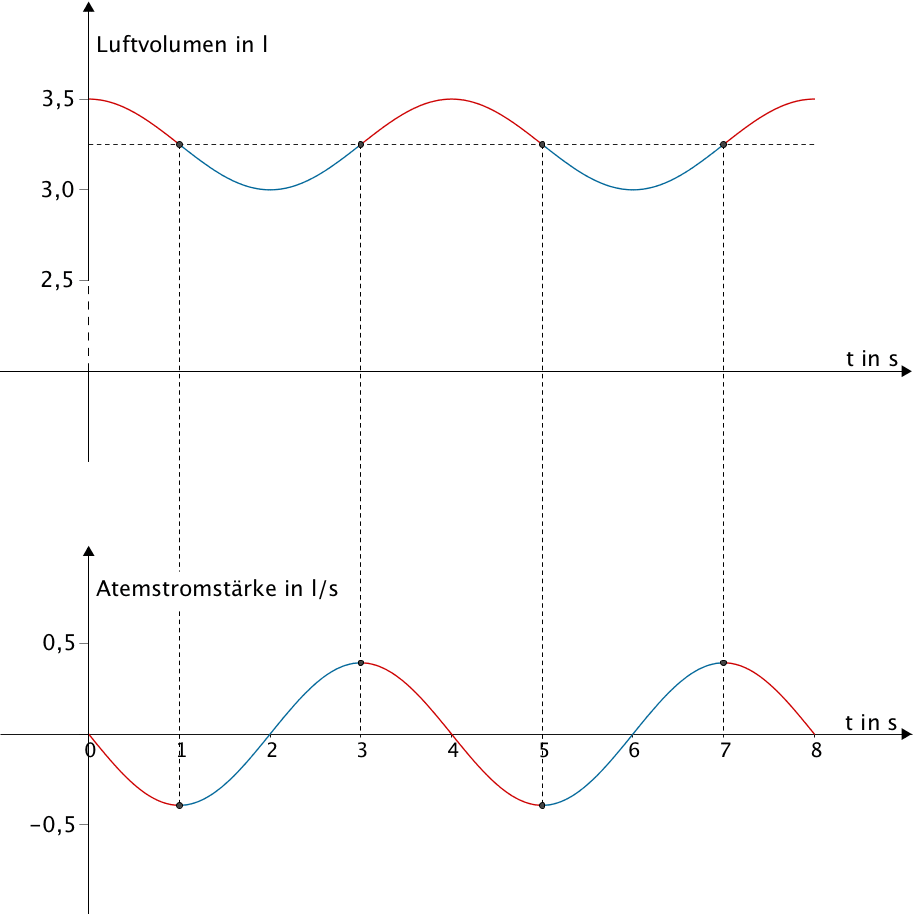
Monotonieverhalten des Graphen der Funktion \(g\) (Atemstromstärke) und Krümmungsverhalten des Graphen der Integralfunktion \(V\) (Luftvolumen).
Für \(t \in [0;1]\) (t in Sekunden) ist der Graph der Funktion \(g\) streng monoton fallend.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\Longrightarrow \quad g'(x) = V''(x) < 0\]
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(V\) ist für \(t \in [0;1]\) rechtsgekrümmt.
Für \(t \in [1;3]\) (t in Sekunden) ist der Graph der Funktion \(g\) streng monoton steigend.
\[\Longrightarrow \quad g'(x) = V''(x) > 0\]
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(V\) ist für \(t \in [1;3]\) linksgekrümmt.
Für \(t \in [3;5]\) (t in Sekunden) ist der Graph der Funktion \(g\) streng monoton fallend.
\[\Longrightarrow \quad g'(x) = V''(x) < 0\]
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(V\) ist für \(t \in [3;5]\) rechtsgekrümmt.
Für \(t \in [5;7]\) (t in Sekunden) ist der Graph der Funktion \(g\) streng monoton steigend.
\[\Longrightarrow \quad g'(x) = V''(x) > 0\]
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(V\) ist für \(t \in [5;7]\) linksgekrümmt.
Für \(t \in [7;8]\) (t in Sekunden) ist der Graph der Funktion \(g\) streng monoton fallend.
\[\Longrightarrow \quad g'(x) = V''(x) < 0\]
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(V\) ist für \(t \in [7;8]\) rechtsgekrümmt.
Ergänzung: Funktionsterm der Funktion, die den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt
Im Folgenden sei \(V\) die Integralfunktion, welche den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson beschreibt.
Stammfunktionen \(G\) der Funktion \(g\) (siehe Teilaufgabe 3c):
\[G(t) = \frac{1}{4}\cos\left( \frac{\pi}{2}t \right) + C\]
Wie bereits erwähnt, ist die Integralfunktion \(V\) eine Stammfunktion von \(g\). Laut der Angabe zu Teilaufgabe 1d befinden sich zu Beginn eines Ausatemvorgangs 3,5 Liter Luft in der Lunge der Testperson. Folglich ist die Integralfunktion \(V\) diejenige Stammfunktion \(G\) von \(g\), für die gilt: \(G(0) = 3{,}5\). Damit lässt sich der Funktionsterm der Integralfunktion \(V\) integralfrei bestimmen.
\[\begin{align*} G(t) &= \frac{1}{4}\cos\left( \frac{\pi}{2}t \right) + C \\[0.8em] 3{,}5 &= \frac{1}{4}\cos\left( \frac{\pi}{2} \cdot 0 \right) + C \\[0.8em] 3{,}5 &= \frac{1}{4} \cdot 1 + C & &| - 0{,}25 \\[0.8em] 3{,}25 &= C \end{align*}\]
\[\Longrightarrow \quad G_{3{,}25}(t) = \frac{1}{4}\cos\left( \frac{\pi}{2}t \right) + 3{,}25\]
\[\Longrightarrow \quad V(t) = \frac{1}{4}\cos\left( \frac{\pi}{2}t \right) + 3{,}25\]
Der Graph \(G_{V}\) der Funktion \(\displaystyle V \colon t \mapsto \frac{1}{4}\cos\left( \frac{\pi}{2}t \right) + 3{,}25\) mit Definitionsmenge \(\mathbb R_{0}^{+}\) beschreibt den zeitlichen Verlauf des Luftvolumens in der Lunge der Testperson.


