Welche Lagebeziehung muss eine Gerade zur Ebene \(E\) haben, wenn für jeden Punkt \(P\) dieser Geraden die Pyramide \(ABCP\) das gleiche Volumen wie die Pyramide \(ABCS\) besitzen soll? Begründen Sie Ihre Antwort.

(3 BE)

Lösung zu Teilaufgabe e

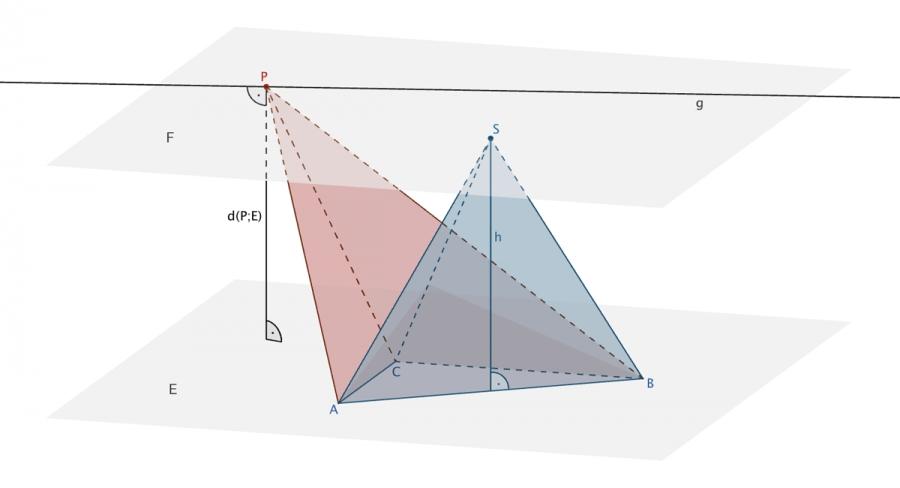
Das Volumen einer Pyramide \(ABCP\) mit fester Grundfläche \(ABC\) ist nur von der Höhe der Pyramide abhängig (schematische Darstellung).

\[V = \frac{1}{3} \cdot A_{ABC} \cdot h\]

Für gleiche Volumen der Pyramiden \(ABCS\) und \(ABCP\) muss demnach gelten:

\(d\,(P; E) = d\,(S; E) = h = 12\) (vgl. Teilaufgabe d)

Folglich liegen alle Geraden \(g\) mit \(P \in g\) im Abstand 12 in einer zur Ebene \(E\) parallelen Ebene \(F\).

\[g \subset F\,; \enspace F \parallel E\,; \enspace d\,(F;E) = d\,(P;E) = d\,(S;E) = h = 12\]