Beurteilen Sie die folgende Aussage:
Der Graph von \(F\) verläuft vollständig unterhalb der \(x\)-Achse.
(3 BE)
Lösung zu Teilaufgabe 1e
\[F(x) = 4x - \underbrace{4 \cdot \underbrace{\ln{(e^x+1)}}_{>\,x}}_{>\,4x} \textcolor{#cc071e}{<} 0\]
Die Aussage ist richtig.
Ergänzende Erklärung (nicht verlangt)
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) ist in \(\mathbb R^+\) streng monoton zunehmend. Deswegen ist der Wert des Terms \(\ln{(e^x+1)}\) stets größer als der Wert des Terms \(\ln{(e^x)} = x\). Somit ist der Wert der Differenz \(4x - 4 \cdot \ln{(e^x+1)}\) für alle \(x \in \mathbb R\) negativ und der Graph von \(F\) verläuft vollständig unterhalb der \(\textcolor{#cc071e}{x}\)-Achse.
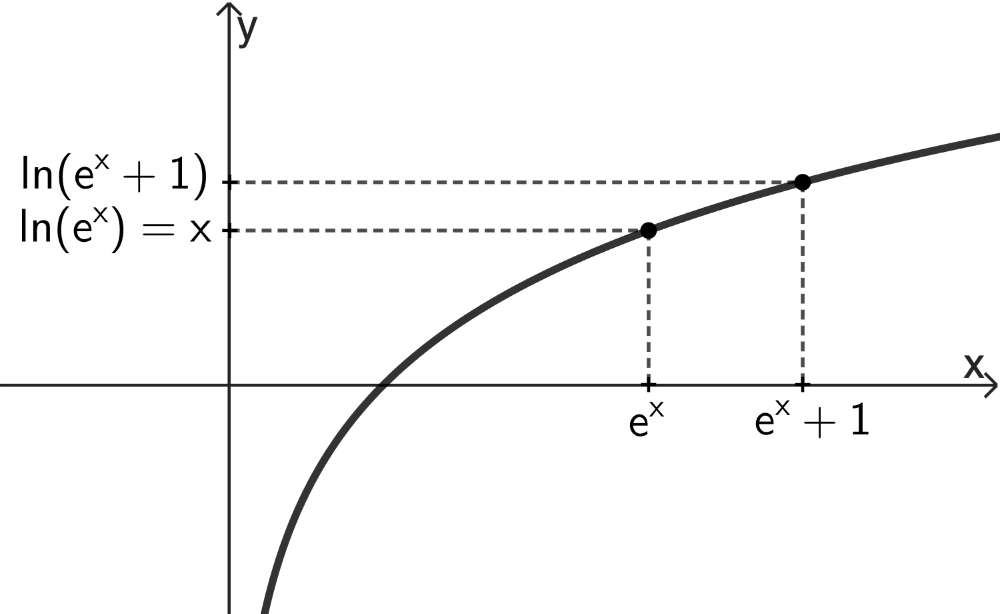
Veranschaulichung der Ungleichung \(\ln{(e^x+1)} > \ln{(e^x)} = x\)


