Geben Sie das Verhalten von \(g\) für \(x \to -\infty\) und \(x \to +\infty\) an.
(2 BE)
Lösung zu Teilaufgabe 2b
\[g(x) = x \cdot e^{-2x}\,, \quad D_g = \mathbb R\]
Verhalten von \(g\) für \(x \to -\infty\)
\[\lim \limits_{x \, \to \, -\infty} g(x) = \lim \limits_{x \, \to \, -\infty} \enspace \underset{\to \, -\infty }{x} \cdot \; \underbrace{e^{-2x}}_{\to \, +\infty} = -\infty\]
Verhalten von \(g\) für \(x \to +\infty\)
\[\lim \limits_{x \, \to \, +\infty} g(x) = \lim \limits_{x \, \to \, +\infty} \enspace \underset{\to \, +\infty}{x} \cdot \; \underbrace{e^{-2x}}_{\to \, 0}\]
Die Grenzwertbetrachtung führt auf den unbestimmten Ausdruck \(\,\infty \cdot 0\,\).
1. Lösungsansatz: Wichtiger Grenzwert (siehe Merkhilfe)
Wichtiger Grenzwert
\[\lim \limits_{x \, \to \, +\infty} \frac{x^r}{e^x} = 0 \enspace (r > 0)\]
Für \(\,x \to +\infty\,\) wächst \(e^x\) „schneller" als jede Potenz \(x^r \enspace (r > 0)\).
(vgl. Merkhilfe)
\[\lim \limits_{x \, \to \, +\infty} x \cdot e^{-2x} = \lim \limits_{x \, \to \, +\infty} \frac{x}{e^{2x}} = 0\]
Für \(x \to + \infty\) wächst \(e^{2x}\) schneller als \(x\).
2. Lösungsansatz: Regel von L'Hospital anwenden
Regel von L'Hospital
Führt der Grenzwert \(\,\displaystyle \lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)}\,\) auf den unbestimmten Ausdruck \(\displaystyle \,\frac{0}{0}\,\) oder \(\displaystyle \,\frac{\infty}{\infty}\,\),
und existiert der Grenzwert \(\displaystyle \,\lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\,\), so gilt:
\[\lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)} = \lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\]
Die Regel kann anstelle \(\,x \to x_0\,\) auch für \(\,x \to \infty\,\) oder \(\,x \to -\infty\,\) angewendet werden.
\[g(x) = x \cdot x^{-2x} = \frac{x}{e^{2x}}\]
\[\lim \limits_{x \, \to \, +\infty} g(x) = \lim \limits_{x \, \to \, +\infty} \; \frac{\overset{\to \, +\infty}{x}}{\underbrace{e^{2x}}_{\to \, +\infty}}\]
Der Grenzwert führt auf den unbestimmten Ausdruck \(\, \displaystyle \frac{\infty}{\infty}\,\).
Ableitung des Zählerterms und des Nennerterms bestimmen:
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
(vgl. Merkhilfe)
\[(x)' = 1\]
\[(e^{2x})' = 2 \cdot e^{2x}\]
Regel von L'Hospital anwenden:
Regel von L'Hospital
Führt der Grenzwert \(\,\displaystyle \lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)}\,\) auf den unbestimmten Ausdruck \(\displaystyle \,\frac{0}{0}\,\) oder \(\displaystyle \,\frac{\infty}{\infty}\,\),
und existiert der Grenzwert \(\displaystyle \,\lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\,\), so gilt:
\[\lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)} = \lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\]
Die Regel kann anstelle \(\,x \to x_0\,\) auch für \(\,x \to \infty\,\) oder \(\,x \to -\infty\,\) angewendet werden.
\[\lim \limits_{x \, \to \, +\infty} g(x) = \lim \limits_{x \, \to \, +\infty} \; \frac{x}{e^{2x}} = \lim \limits_{x \, \to \, +\infty} \; \frac{1}{2 \cdot \underbrace{e^{2x}}_{\to \, +\infty}} = 0\]
Anmerkung:
Die Regel von L'Hospital ist nicht im G8 Mathematik Lehrplan enthalten. Erfahrungsgemäß wird diese aber des Öfteren optional unterrichtet, um Grenzwertbetrachtungen von unbestimmten Ausdrücken der Form \(\dfrac{0}{0}\) oder \(\dfrac{\infty}{\infty}\) zu vertiefen.
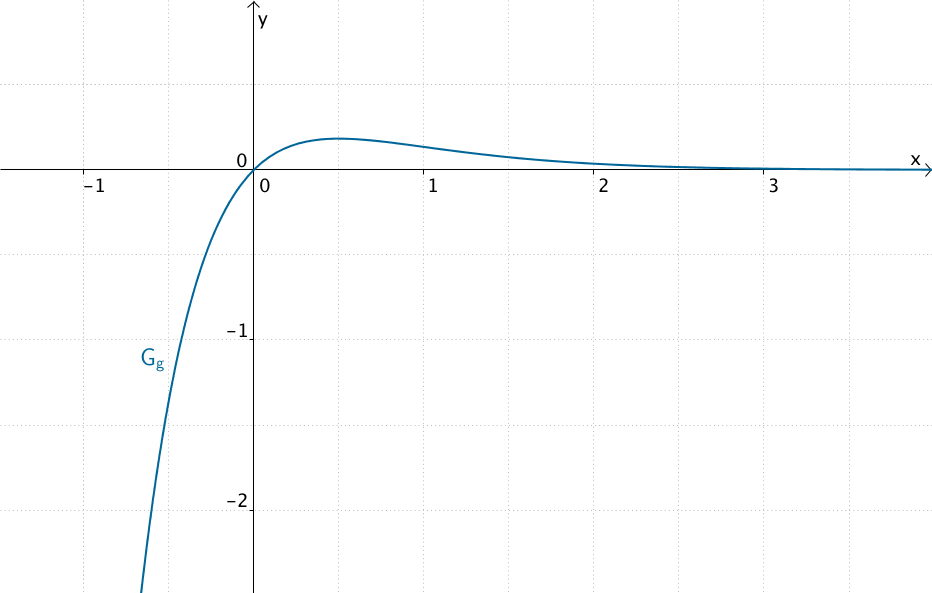
Der Graph der Funktion \(\,g\,\) verläuft für \(\,x \to -\infty\,\) gegen \(\,-\infty\,\) und nähert sich für \(\,x \to +\infty\,\) asymptotisch der \(x\)-Achse an.


