Ein Laplace-Tetraeder (dreiseitige Pyramide mit vier kongruenten gleichseitigen Dreiecken) ist auf seinen vier Flächen mit je einer der Ziffern 1 bis 4 beschriftet. Es wird folgendes Spiel gespielt:
Ein Spieler zahlt einen Einsatz in Höhe von 1 Euro. Dann setzt er auf eine der Ziffern 1, 2, 3 oder 4 und wirft das Tetraeder anschließend dreimal. Gewertet wird die Ziffer der Fläche, auf der das Tetraeder zu liegen kommt.
Erzielt der Spieler bei keinem Wurf die gesetzte Ziffer, ist der Einsatz verloren.
Erzielt der Spieler einmal die gesetzte Ziffer, erhält er den Einsatz zurück.
Erzielt der Spieler zweimal die gesetzte Ziffer, erhält er den doppelten Einsatz zurück.
Erzielt der Spieler dreimal die gesetzte Ziffer, erhält er den dreifachen Einsatz zurück.
Die Zufallsgröße \(G\) beschreibt den Gewinn eines Spielers pro Spiel in Euro.
a) Ermitteln Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\).
b) Berechnen Sie den Erwartungswert der Zufallsgröße \(G\) und interpretieren Sie das Ergebnis im Sachzusammenhang.
a) Wahrscheinlichkeitsverteilung der Zufallsgroße \(G\)
Veranschaulichung des Spiels mithilfe eines Baumdiagramms:
Betrachtet werden folgende Ereignisse:
\(Z\): „Der Spieler erzielt die gesetzte Zahl."
\(\overline{Z}\): „Der Spieler erzielt die gesetzte Zahl nicht."
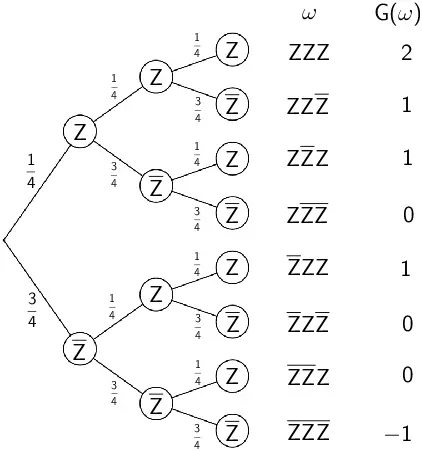
Es gibt pro Wurf des Tetraeders vier gleichwahrscheinliche Möglichkeiten, eine der Ziffern 1, 2, 3 oder 4 zu erzielen. Damit beträgt die Wahrscheinlichkeit dafür, dass ein Spieler die gesetzte Zahl erzielt bei jedem Wurf \(P(Z) = \frac{1}{4}\) (vgl. Abiturskript - 3.1.3 Laplace-Experiment, Laplace-Wahrscheinlichkeit). Gemäß der Knotenregel gilt: \(P(\overline{Z}) = \frac{3}{4}\) (vgl. Abiturskript - 3.1.4 Baumdiagramm und Vierfeldertafel).
Unter Anwendung der ersten bzw. zweiten Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(G = 2) = P(\{ZZZ\}) = \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} = \left( \frac{1}{4} \right)^{3} = \frac{1}{64}\]
\[\begin{align*}P(G = 1) &= P(\{ZZ\overline{Z}\}) + P(\{Z\overline{Z}Z\}) + P(\{\overline{Z}ZZ\}) \\[0.8em] &= \underbrace{\underbrace{\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{3}{4}}_{\large{\text{1. Pfadregel}}} + \underbrace{\frac{1}{4} \cdot \frac{3}{4} \cdot \frac{1}{4}}_{\large{\text{1. Pfadregel}}} + \underbrace{\frac{3}{4} \cdot \frac{1}{4} \cdot \frac{1}{4}}_{\large{\text{1. Pfadregel}}}}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= 3 \cdot \left( \frac{1}{4} \right)^{2} \cdot \frac{3}{4} \\[0.8em] &= \frac{9}{64}\end{align*}\]
\[\begin{align*}P(G = 0) &= P(\{Z\overline{Z}\overline{Z}\}) + P(\{\overline{Z}Z\overline{Z}\}) + P(\{\overline{Z}\overline{Z}Z\}) \\[0.8em] &= \underbrace{\underbrace{\frac{1}{4} \cdot \frac{3}{4} \cdot \frac{3}{4}}_{\large{\text{1. Pfadregel}}} + \underbrace{\frac{3}{4} \cdot \frac{1}{4} \cdot \frac{3}{4}}_{\large{\text{1. Pfadregel}}} + \underbrace{\frac{3}{4} \cdot \frac{3}{4} \cdot \frac{1}{4}}_{\large{\text{1. Pfadregel}}}}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= 3 \cdot \frac{1}{4} \cdot \left( \frac{3}{4} \right)^{2} \\[0.8em] &= \frac{27}{64}\end{align*}\]
\[P(G = -1) = P(\{\overline{Z}\overline{Z}\overline{Z}\}) = \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} = \left( \frac{3}{4} \right)^{3} = \frac{27}{64}\]
Veranschaulichung als Verteilungstabelle:
| \(G = g_{i}\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(P(G = g_{i})\) | \(\dfrac{27}{64}\) | \(\dfrac{27}{64}\) | \(\dfrac{9}{64}\) | \(\dfrac{1}{64}\) |
Probe:
Die Summe der Wahrscheinlichkeiten \(P(G = g_{i})\) aller Werte \(g_{i}\) der Zufallsgröße \(G\) ist gleich Eins.
\[\sum_{i\,=\,1}^{n}P(G = g_{i}) = \frac{27}{64} + \frac{27}{64} + \frac{9}{64} + \frac{1}{64} = 1\]
b) Erwartungswert der Zufallsgröße \(G\) und Interpretation des Ergebnisses im Sachzusammenhang
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*} E(G) &= g_{1} \cdot p_{1} + g_{2} \cdot p_{2} + g_{3} \cdot p_{3} + g_{4} \cdot p_{4} \\[0.8em] &= (-1) \cdot \frac{27}{64} + 0 \cdot \frac{27}{64} + 1 \cdot \frac{9}{64} + 2 \cdot \frac{1}{64} \\[0.8em] &= -\frac{27}{64} + \frac{9}{64} + \frac{2}{64} \\[0.8em] &= -\frac{16}{64} \\[0.8em] &= -\frac{1}{4} \end{align*}\]
Interpretation des Ergebnisses im Sachzusammenhang:
Das Ergebnis \(E(G) = -\frac{1}{4}\) bedeutet, dass ein Spieler im Mittel pro Spiel 25 Cent verliert.

