Gegeben sind die Punkte \(A(4|-2|-1)\), \(B(2|4|5)\) und \(C(5|-6|3)\).
a) Ermitteln Sie die Größe des Innenwinkels \(\alpha\) des Dreiecks \(ABC\).
b) Geben Sie die Gleichung der Kugel \(K\) mit dem Mittelpunkt \(C\) in Koordinatendarstellung an, auf deren Oberfläche der Punkt \(A\) liegt. Untersuchen Sie mithilfe der Kugelgleichung, ob der Punkt \(B\) innerhalb der Kugel \(K\), auf der Kugeloberfläche von \(K\) oder außerhalb von \(K\) liegt.
a) Größe des Innenwinkels \(\alpha\) des Dreiecks \(ABC\)
Planskizze:
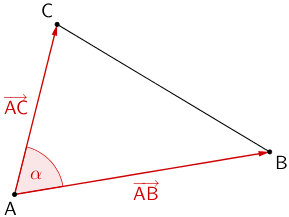
Der Innenwinkel \(\alpha\) des Dreiecks \(ABC\) ist gleich dem Winkel zwischen den Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\).
Anwendung des Skalarprodukts:
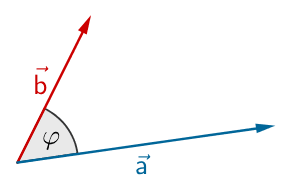
Winkel zwischen zwei Vektoren (vgl. Merkhilfe)
\[\cos \varphi = \frac{\overrightarrow{a} \circ \overrightarrow{b}}{\vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert}\,; \quad \varphi \in [0;\pi]\]
\[\cos{\alpha} = \frac{\overrightarrow{AB} \circ \overrightarrow{AC}}{\vert \overrightarrow{AB} \vert \cdot \vert \overrightarrow{AC} \vert}\]
Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) berechnen:
\(A(4|-2|-1)\), \(B(2|4|5)\), \(C(5|-6|3)\)
\[\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} = \begin{pmatrix} 2 \\ 4 \\ 5 \end{pmatrix} - \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} = \begin{pmatrix} -2 \\ 6 \\ 6 \end{pmatrix}\]
\[\overrightarrow{AC} = \overrightarrow{C} - \overrightarrow{A} = \begin{pmatrix} 5 \\ -6 \\ 3 \end{pmatrix} - \begin{pmatrix} 4 \\ -2 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ -4 \\ 4 \end{pmatrix}\]
Innenwinkel \(\alpha\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \cos{\alpha} &= \frac{\overrightarrow{AB} \circ \overrightarrow{AC}}{\vert \overrightarrow{AB} \vert \cdot \vert \overrightarrow{AC} \vert} \\[0.8em] &= \frac{\begin{pmatrix} -2 \\ 6 \\ 6 \end{pmatrix} \circ \begin{pmatrix} 1 \\ -4 \\ 4 \end{pmatrix}}{\left| \begin{pmatrix} -2 \\ 6 \\ 6 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 1 \\ -4 \\ 4 \end{pmatrix} \right|} \\[0.8em] &= \frac{(-2) \cdot 1 + 6 \cdot (-4) + 6 \cdot 4}{\sqrt{(-2)^{2} + 6^{2} + 6^{2}} \cdot \sqrt{1^{2} + (-4)^{2} + 4^{2}}} \\[0.8em] &= \frac{-2}{\sqrt{76} \cdot \sqrt{33}} \\[0.8em] &\approx -0{,}040 & &| \; \text{TR:} \; \cos^{-1}(\dots) \\[2.4em] \alpha &\approx 92{,}29^{\circ} \end{align*}\]
b) Gleichung der Kugel \(K\) mit Mittelpunkt \(C\) und \(A \in K\) in Koordinatendarstellung sowie Untersuchung der Lage des Punktes \(B\) bezüglich \(K\)
Gleichung der Kugel \(K\) mit Mittelpunkt \(C\) und \(A \in K\) in Koordinatendarstellung
Anmerkung:
Die Gleichung der Kugel \(K\) ist lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.
Der Radius \(r\) der Kugel \(K\) ist gleich dem Betrag des Verbindungsvektors \(\overrightarrow{AC}\) oder dessen Gegenvektor \(\overrightarrow{CA}\).
\(r = \vert \overrightarrow{AC} \vert = \sqrt{33}\) (vgl. Teilaufgabe a)
\(C(5|-6|3)\)
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[\begin{align*} &K \colon (x_{1} - c_{1})^{2} + (x_{2} - c_{2})^{2} + (x_{3} - c_{3})^{2} = r^{2} \\[0.8em] &K \colon (x_{1} - c_{1})^{2} + (x_{2} - c_{2})^{2} + (x_{3} - c_{3})^{2} = {\vert \overrightarrow{AC} \vert}^{2} \\[0.8em] &K \colon (x_{1} - 5)^{2} + (x_{2} + 6)^{2} + (x_{3} - 3)^{2} = {\sqrt{33}}^{2} \\[0.8em] &K \colon (x_{1} - 5)^{2} + (x_{2} + 6)^{2} + (x_{3} - 3)^{2} = 33 \end{align*}\]
Untersuchung der Lage des Punktes \(B\) bezüglich der Kugel \(K\) mithilfe der Kugelgleichung
Es wird die Punktprobe \(B \in K\) durchgeführt. Folgende drei Fälle sind möglich:
\[B \notin K \colon (b_{1} - 5)^{2} + (b_{2} + 6)^{2} + (b_{3} - 3)^{2} < 33\]
Der Punkt \(B\) liegt innerhalb der Kugel \(K\).
\[B \in K \colon (b_{1} - 5)^{2} + (b_{2} + 6)^{2} + (b_{3} - 3)^{2} = 33\]
Der Punkt \(B\) liegt auf der Kugeloberfläche.
\[B \notin K \colon (b_{1} - 5)^{2} + (b_{2} + 6)^{2} + (b_{3} - 3)^{2} > 33\]
Der Punkt \(B\) liegt außerhalb der Kugel \(K\).
Punktprobe:
\(B(2|4|5)\)
\[\begin{align*}(b_{1} - 5)^{2} + (b_{2} + 6)^{2} + (b_{3} - 3)^{2} &= (2 - 5)^{2} + (4 + 6)^{2} + (5 - 3)^{2} \\[0.8em] &= (-3)^{2} + 10^{2} + 2^{2} \\[0.8em] &= 113\end{align*}\]
\[\Longrightarrow \quad 113 > 33\]
\(\Longrightarrow \quad\)Derr Punkt \(B\) liegt außerhalb der Kugel \(K\).

