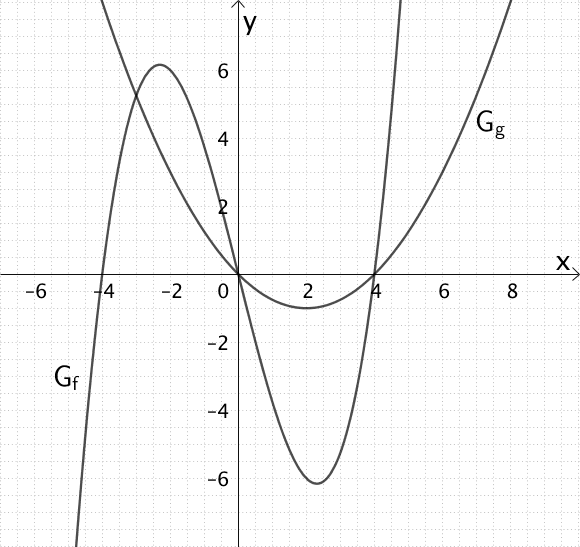
Gegeben sind die Funktionen \(f \colon x \mapsto \dfrac{1}{4}x^{3} - 4x\) und \(g \colon x \mapsto \dfrac{1}{4}x^{2} - x\). Die Abbildung zeigt den Graphen \(G_{f}\) der Funktion \(f\) sowie den Graphen \(G_{g}\) der Funktion \(g\).
a) Berechnen Sie den Flächeninhalt \(A\) der von den Graphen \(G_{f}\) und \(G_{g}\) begrenzten Fläche.
b) Geben Sie ohne weitere Rechnung den Wert des Integrals \(\displaystyle \int_{-4}^{+4} f(x) dx\) an und veranschaulichen Sie Ihr Ergebnis in der Abbildung durch geeignete Eintragungen.
a) Berechnung des Flächeninhalts \(A\) der von den Graphen \(G_{f}\) und \(G_{g}\) begrenzten Fläche
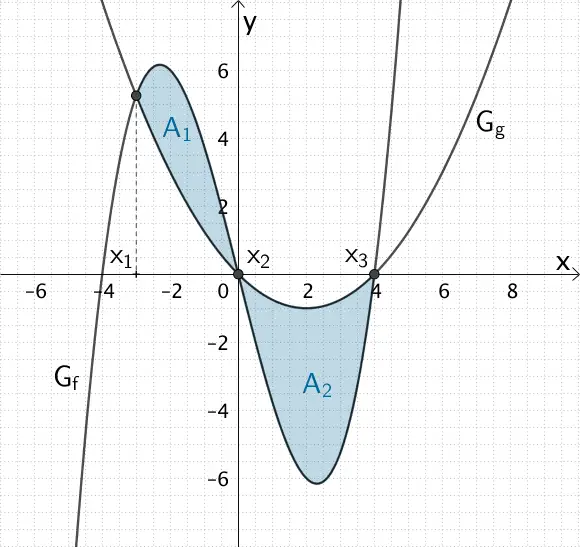
Die Abbildung zeigt, dass sich die Graphen \(G_{f}\) und \(G_{g}\) an den Stellen \(x_{1}\), \(x_{2}\) und \(x_{3}\) schneiden.
Für die Berechnung des Flächeninhalts \(A\) werden die Flächeninhalte \(A_{1}\) und \(A_{2}\) der Teilflächen in den Intervallen \([x_{1};x_{2}]\) und \([x_{2};x_{3}]\) addiert. Hierfür wird über die Differenzfunktion \(f(x) - g(x)\) bzw. \(g(x) - f(x)\) integriert, wobei die Schnittstellen \(x_{1}\), \(x_{2}\) und \(x_{3}\) die Intergrationsgrenzen bilden..
Um jeweils einen positiven Wert für den Flächeninhalt der Teilflächen zu erhalten, wählt man den Betrag der Integrale. Eine Berücksichtigung, ob \(G_{f}\) oberhalb \(G_{g}\) verläuft oder umgekehrt, kann somit entfallen.
\[\begin{align*} A &= A_{1} + A_{2} \\[0.8em] &= \int_{x_{1}}^{x_{2}} \Big[\underbrace{f(x) - g(x)}_{\large{f(x) \,>\, g(x)}}\Big] dx + \int_{x_{2}}^{x_{3}} \Big[\underbrace{g(x) - f(x)}_{\large{g(x) \,>\, f(x)}} \Big] dx \\[0.8em] &= \left| \int_{x_{1}}^{x_{2}} \left[ f(x) - g(x) \right] dx \right| + \left| \int_{x_{2}}^{x_{3}} \left[ f(x) - g(x) \right] dx \right| \end{align*}\]
Schnittstellen der Graphen \(G_{f}\) und \(G_{g}\) berechnen:
Für die Berechnung der Schnittstellen von \(G_{f}\) und \(G_{g}\) werden die Funktionsterme \(f(x)\) und \(g(x)\) gleichgesetzt.
\[f(x) = \frac{1}{4}x^{3} - 4x; \; D_{f} = \mathbb R\]
\[g(x) = \frac{1}{4}x^{2} - x; \; D_{g} = \mathbb R\]
\[\begin{align*} f(x) &= g(x) \\[0.8em] \frac{1}{4}x^{3} - 4x &= \frac{1}{4}x^{2} - x &&| -\frac{1}{4}x^{2} + x \\[0.8em] \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x &= 0 \\[0.8em] \frac{1}{4}x\left( x^{2} - x - 12 \right) &= 0 \end{align*}\]
Satz vom Nullsprodukt:
Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist.
\[\Longrightarrow \quad x_{1} = 0 \enspace \vee \enspace x^{2} - x - 12 = 0\]
Lösungsformel für quadratische Gleichungen anwenden:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{2,3} &= \frac{1 \pm \sqrt{(-1)^{2} - 4 \cdot 1 \cdot (-12)}}{2 \cdot 1} \\[0.8em] &= \frac{1 \pm 7}{2}\end{align*}\]
\[x_{2} = -3; \; x_{3} = 4\]
Die Schnittstellen der Graphen \(G_{f}\) und \(G_{g}\) sind \(x_{1} = -3\), \(x_{2} = 0\) und \(x_{3} = 4\) (aufsteigend sortiert und nummeriert).
Damit ergibt sich der Flächeninhalt \(A\) zu:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[f(x) = \frac{1}{4}x^{3} - 4x; \; D_{f} = \mathbb R\]
\[g(x) = \frac{1}{4}x^{2} - x; \; D_{g} = \mathbb R\]
\[\begin{align*} A &= \left| \int_{-3}^{0} \left[ f(x) - g(x) \right] dx \right| + \left| \int_{0}^{4} \left[ f(x) - g(x) \right] dx \right| \\[0.8em] &= \left| \int_{-3}^{0} \left[ \frac{1}{4}x^{3} - 4x - \left( \frac{1}{4}x^{2} - x \right) \right] dx \right| + \left| \int_{0}^{4} \left[ \frac{1}{4}x^{3} - 4x - \left( \frac{1}{4}x^{2} - x \right) \right] dx \right| \\[0.8em] &= \left| \int_{-3}^{0} \left( \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x \right) dx \right| + \left| \int_{0}^{4} \left( \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x \right) dx \right| \end{align*}\]
Für die Berechnung der bestimmten Integrale wird eine Stammfunktion der Integrandenfunktion \(x \mapsto \dfrac{1}{4}x^{3} - \dfrac{1}{4}x^{2} - 3x\) benötigt. Die Menge aller Stammfunktionen ist gegeben durch das unbestimmte Integral \(\displaystyle \int \left( \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x \right) dx\).
Unter Anwendung des wichtigen unbestimmten Integrals \(\displaystyle \int x^r \,dx = \dfrac{x^{r + 1}}{r + 1} + C \quad (r \neq -1)\) ergibt sich:
Wichtiges unbestimmtes Integral:
\[\int x^r \,dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq -1)\]
\[C \in \mathbb R\]
(vgl. Merkhilfe)
\[\begin{align*}\int \left( \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x \right) dx &= \frac{1}{4} \cdot \frac{x^{4}}{4} - \frac{1}{4} \cdot \frac{x^{3}}{3} - 3 \cdot \frac{x^{2}}{2} + C \\[0.8em] &= \frac{1}{16}x^{4} - \frac{1}{12}x^{3} - \frac{3}{2}x^{2} + C \end{align*}\]
Für \(C = 0\) ist die Funktion \(x \mapsto \dfrac{1}{16}x^{4} - \dfrac{1}{12}x^{3} - \dfrac{3}{2}x^{2}\) eine Stammfunktion der Integrandenfunktion \(x \mapsto \dfrac{1}{4}x^{3} - \dfrac{1}{4}x^{2} - 3x\).
Flächeninhalt \(A\) berechnen:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} A = \quad &\left| \int_{-3}^{0} \left( \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x \right) dx \right| + \left| \int_{0}^{4} \left( \frac{1}{4}x^{3} - \frac{1}{4}x^{2} - 3x \right) dx \right| \\[0.8em] = \quad &\left| \left[ \frac{1}{16}x^{4} - \frac{1}{12}x^{3} - \frac{3}{2}x^{2} \right]_{-3}^{0} \right| + \left| \left[ \frac{1}{16}x^{4} - \frac{1}{12}x^{3} - \frac{3}{2}x^{2} \right]_{0}^{4} \right| \\[0.8em] = \quad &\left| \frac{1}{16} \cdot 0^{4} - \frac{1}{12} \cdot 0^{3} - \frac{3}{2} \cdot 0^{2} - \left( \frac{1}{16} \cdot (-3)^{4} - \frac{1}{12} \cdot (-3)^{3} - \frac{3}{2} \cdot (-3)^{2} \right) \right| \\[0.8em] +\; &\left| \frac{1}{16} \cdot 4^{4} - \frac{1}{12} \cdot 4^{3} - \frac{3}{2} \cdot 4^{2} - \left( \frac{1}{16} \cdot 0^{4} - \frac{1}{12} \cdot 0^{3} - \frac{3}{2} \cdot 0^{2} \right) \right| \\[0.8em] = \quad &\left| 0 - \left( \frac{81}{16} - \left( -\frac{27}{12} \right) - \frac{27}{2} \right) \right| + \left| \frac{256}{16} - \frac{64}{12} - \frac{48}{2} - 0 \right| \\[0.8em] = \quad &\left| -\frac{99}{16} \right| + \left| -\frac{40}{3} \right| \\[0.8em] = \quad &\frac{99}{16} + \frac{40}{3} \\[0.8em] = \quad &\frac{937}{46} \\[0.8em] \approx \quad &19{,}52 \end{align*}\]
Der Flächeninhalt \(A\) der von den Graphen \(G_{f}\) und \(G_{g}\) begrenzten Fläche beträgt ca. 19,52 FE (Flächeneinheiten).
b) Wert des Integrals \(\displaystyle \int_{-4}^{+4} f(x) dx\) und Veranschaulichung des Ergebnisses
\[\int_{-4}^{+4} f(x) dx = 0\]
![Flächenbilanz der Flächenstücke, welche der Graph der Funktion f im Intervall [-4;+4] mit der x-Achse einschließt. Flächenbilanz der Flächenstücke, welche der Graph der Funktion f im Intervall [-4;+4] mit der x-Achse einschließt.](/images/stories/Klausuren/Klausuren_Q12_1/Klausur_Q12_1-003/Klausur_Q12_1-003_A1_2.png)
Der Wert des Integrals \(\displaystyle \int_{-4}^{+4} f(x) dx\) lässt sich als Flächenbilanz der Flächenstücke interpretieren, welche \(G_{f}\) im Intervall \([-4;+4]\) mit der \(x\)-Achse einschließt. Die Abbildung zeigt, dass \(G_{f}\) punktsymmetrisch zum Koordinatenursprung ist und im Intervall \([-4;+4]\) zwei flächengleiche Flächenstücke mit der \(x\)-Achse einschließt. Das im Intervall \([-4;0]\) oberhalb der \(x\)-Achse liegende Flächenstück zählt positiv und das im Intervall \([0;+4]\) unterhalb der \(x\)-Achse liegende Flächenstück zählt negativ. Die Flächenbilanz der beiden Flächenstücke ist somit gleich Null.

