Begründen Sie mithilfe von Abbildung 1, dass \(F_{1}\) mindestens eine weitere positive Nullstelle hat.
(2 BE)
Lösung zu Teilaufgabe 1e
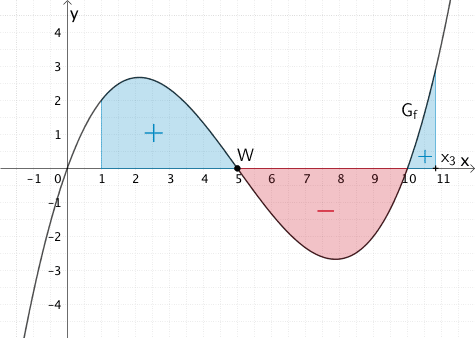
Da \(G_{f}\) punktsymmetrisch zum Wendepunkt \(W(5|0)\) ist (vgl. Teilaufgabe 1b), gilt:
\[ \textcolor{#0087c1}{\int_{1}^{5}f(t)dt} < \textcolor{#cc071e}{\left| \int_{5}^{10} f(t)dt \right|}\]
Da \(G_{f}\) im Intervall \([1;5]\) oberhalb und im Intervall \([5;10]\) unterhalb der \(x\)-Achse verläuft, ist die Flächenbilanz des Integrals \(\displaystyle \int_{1}^{10}f(t)dt\) negativ.
Weil \(G_{f}\) für \(x > 10\) wieder oberhalb der \(x\)-Achse verläuft, gibt es eine dritte positive Nullstelle \(x _{3} \in \; ]10;+\infty[\) sodass die Flächenbilanz von \(\displaystyle F_{1}(x_{3}) = \int_{1}^{x_{3}}f(t)dt\) gleich Null ist.


