Die Abbildung zeigt modellhaft wesentliche Elemente einer Kletteranlage: zwei horizontale Plattformen, die jeweils um einen vertikal stehenden Pfahl gebaut sind, sowie eine Kletterwand, die an einer der beiden Plattformen angebracht ist.
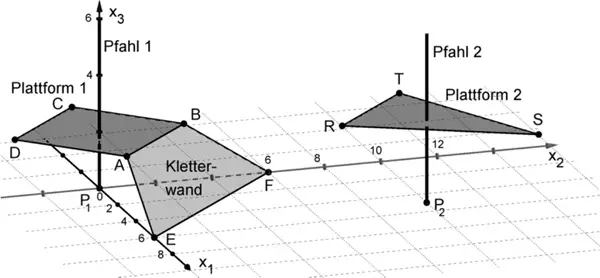
Im verwendeten Koordinatensystem beschreibt die \(x_{1}x_{2}\)-Ebene den horizontalen Untergrund. Die Plattformen und die Kletterwand werden als ebene Vielecke betrachtet. Eine Längeneinheit entspricht 1 m in der Wirklichkeit. Die Punkte, in denen die Pfähle aus dem Untergrund austreten, werden durch \(P_{1}(0|0|0)\) und \(P_{2}(5|10|0)\) dargestellt. Außerdem sind die Eckpunkte \(A(3|0|2)\), \(B(0|3|2)\), \(E(6|0|0)\), \(F(0|6|0)\), \(R(5|7|3)\) und \(T(2|10|3)\) gegeben. Die Materialstärke aller Bauteile der Anlage soll vernachlässigt werden.
In den Mittelpunkten der oberen und unteren Kante der Kletterwand sind die Enden eines Seils befestigt, das 20 % länger ist als der Abstand der genannten Mittelpunkte. Berechnen Sie die Länge des Seils.
(3 BE)
Lösung zu Teilaufgabe a
![Mittelpunkte der Seiten [AB] und [EF] des Vierecks AEFB (Kletterwand) Mittelpunkte der Seiten [AB] und [EF] des Vierecks AEFB (Kletterwand)](/images/stories/B2018_PT_B_G2/B2018_PT_B_G2_a.png)
Die Länge \(l\) des Seils ist gleich der 1,2-fachen Länge (120 %) der Strecke \([M_{EF}M_{AB}]\) der Mittelpunkte \(M_{EF}\) und \(M_{AB}\) der Kanten \([EF]\) und \([AB]\).
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[l = 1{,}2 \cdot \overline{M_{EF}M_{AB}} = 1{,}2 \cdot \vert \overrightarrow{M_{EF}M_{AB}} \vert\]
Ortsvektoren der Mittelpunkte \(M_{EF}\) und \(M_{AB}\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\(A(3|0|2)\), \(B(0|3|2)\), \(E(6|0|0)\), \(F(0|6|0)\)
\[\overrightarrow{M_{AB}} = \frac{1}{2} \cdot (\overrightarrow{A} + \overrightarrow{B}) = \frac{1}{2} \cdot \left[ \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \\ 2 \end{pmatrix} \right] = \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 2 \end{pmatrix}\]
\[\overrightarrow{M_{EF}} = \frac{1}{2} \cdot (\overrightarrow{E} + \overrightarrow{F}) = \frac{1}{2} \cdot \left[ \begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} \right] = \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}\]
Länge \(l\) des Seils berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}l &= 1{,}2 \cdot \vert \overrightarrow{M_{EF}M_{AB}} \vert = 1{,}2 \cdot \vert \overrightarrow{M_{AB}} - \overrightarrow{M_{EF}} \vert \\[0.8em] &= 1{,}2 \cdot \left| \begin{pmatrix} 1{,}5 \\ 1{,}5 \\ 2 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix} \right| = 1{,}2 \cdot \left| \begin{pmatrix} -1{,}5 \\ -1{,}5 \\ 2 \end{pmatrix} \right| \\[0.8em] &= 1{,}2 \cdot \sqrt{(-1{,}5)^{2} + (-1{,}5)^{2} + 2^{2}} = 1{,}2 \cdot \sqrt{8{,}5} \approx 3{,}50 \end{align*}\]
Die Länge des Seils, das die Mittelpunkte der oberen und unteren Kante der Kletterwand verbindet, beträgt ca. 3,50 Meter.


