Abbildung 2 zeigt den Graphen \(G_{k}\) einer in \(\mathbb R\) definierten Funktion \(k\). Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion \(k'\). Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen \(G_{k}\) an dessen Wendepunkt \((0|-3)\) sowie die Nullstelle von \(k'\).
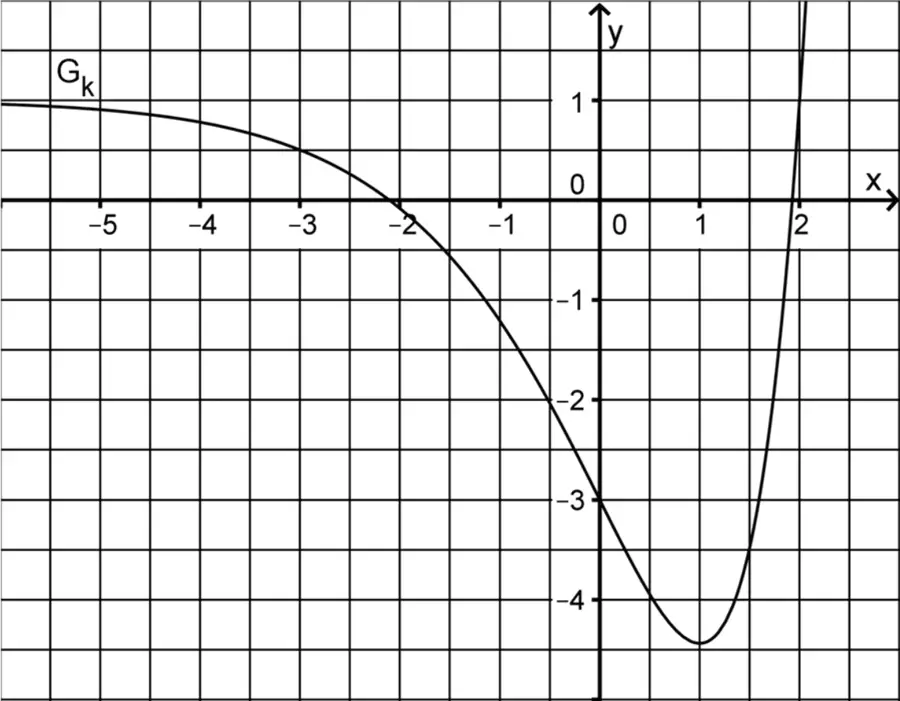
Abb. 2
(4 BE)
Lösung zu Teilaufgabe 4
Die Ableitung \(k'\) beschreibt die Steigung der Tangente an den Graphen der Funktion \(k\). Der Wert der Steigung der Tangente an den Graphen der Funktion \(k\) liefert also an jeder betrachteten Stelle \(x_{0}\) einen Punkt \((x_{0}|k'(x_{0})\) des Graphen der Ableitungsfunktion \(k'\).
Verhalten von \(G_{k'}\) für \(x < 1\) bzw. \(x \to -6\)
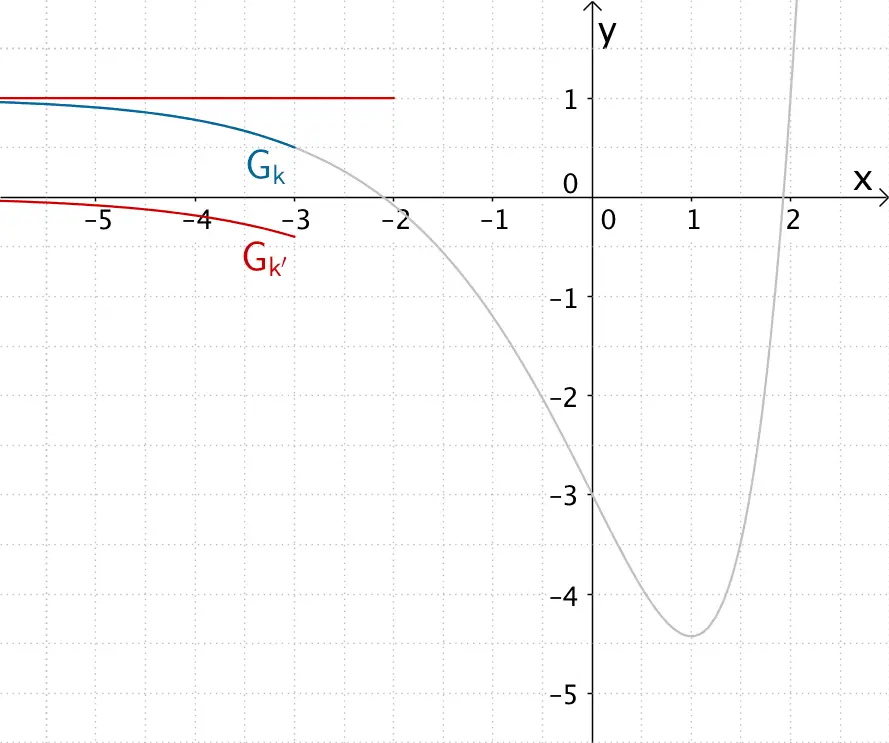
Für \(x < 1\) ist der Graph der Funktion \(k\) streng monoton fallend.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(\Longrightarrow \quad k'(x) < 0\) für \(x < 1\), also verfüllt der Graph der Funktion \(k'\) für \(x < 0\) unterhalb der \(x\)-Achse.
Für \(x \to -6\) verläuft der Graph der Funktion \(k\) tangential zur Geraden mit der Gleichung \(y = 1\). Folglich nimmt die Steigung der Tangente an den Graphen der Funktion \(k\) für \(x \to -6\) den Grenzwert Null an.
\[\lim \limits_{x \, \to \, -6} k'(x) = 0 \]
Der Graph der Funktion \(k'\) nähert sich daher für \(x \to -6\) tangential dem Wert \(y = 0\) an.
Verhalten von \(G_{k'}\) in der Umgebung des Wendepunkts von \(G_{k}\)
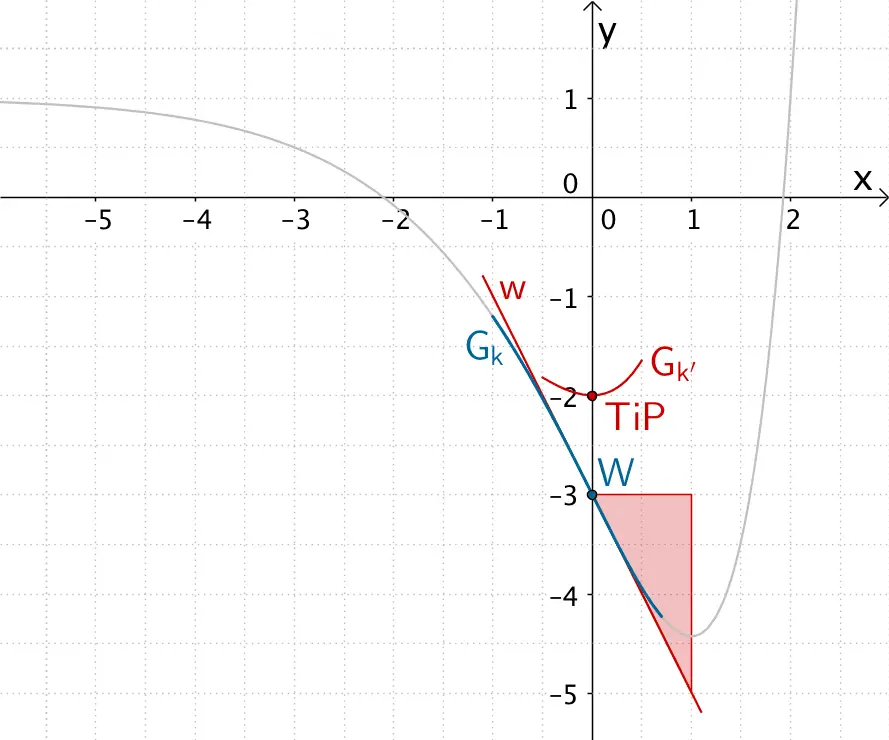
An der Wendestelle \(x_{W} = 0\) besitzt der Graph der Funktion \(k\) den Wendepunkt \(W(0|-3)\) (vgl. Angabe). An dieser Wendestelle erreicht die Steigung der Tangente an den Graphen der Funktion \(k\) (Steigung der Wendetangente \(w\)) ein Minimum.
Das bedeutet, dass der Graph der Ableitungsfunktion \(k'\) an der Wendestelle von \(G_{k}\) einen Tiefpunkt hat.
Die Steigung der Wendetangente \(w\) kann der Abbildung näherungsweise mithilfe eines Steigungsdreiecks zu \(m_{w} \approx -2\) entnommen werden.
Folglich besitzt der Graph der Ableitungsfunktion \(k'\) an der Wendestelle \(x_{W} = 0\) den Tiefpunkt \(TiP(0|-2)\).
Verhalten von \(G_{k'}\) in der Umgebung des Tiefpunkts von \(G_{k}\)
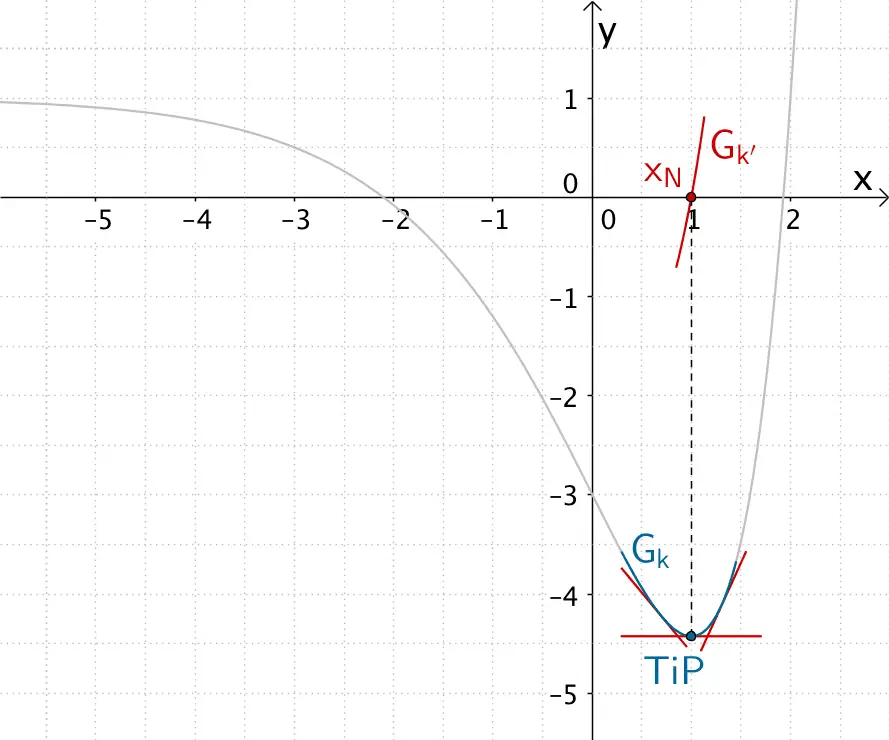
Für \(x = 1\) besitzt der Graph der Funktion \(k\) einen Tiefpunkt \(TiP\). Die Steigung der Tangente an den Graphen der Funktion \(k\) im Tiefpunkt ist gleich Null. In der Umgebung des Tiefpunkts von \(G_{k}\) wechselt die Steigung einer Tangente an \(G_{k}\) das Vorzeichen von \(-\) nach \(+\).
Folglich hat der Graph der Ableitungsfunktion \(k'\) für \(x = 1\) eine einfache Nullstelle \(x_{N}\) mit Vorzeichenwechsel von \(-\) nach \(+\).
Verhalten von \(G_{k'}\) für \(x \to +\infty\)
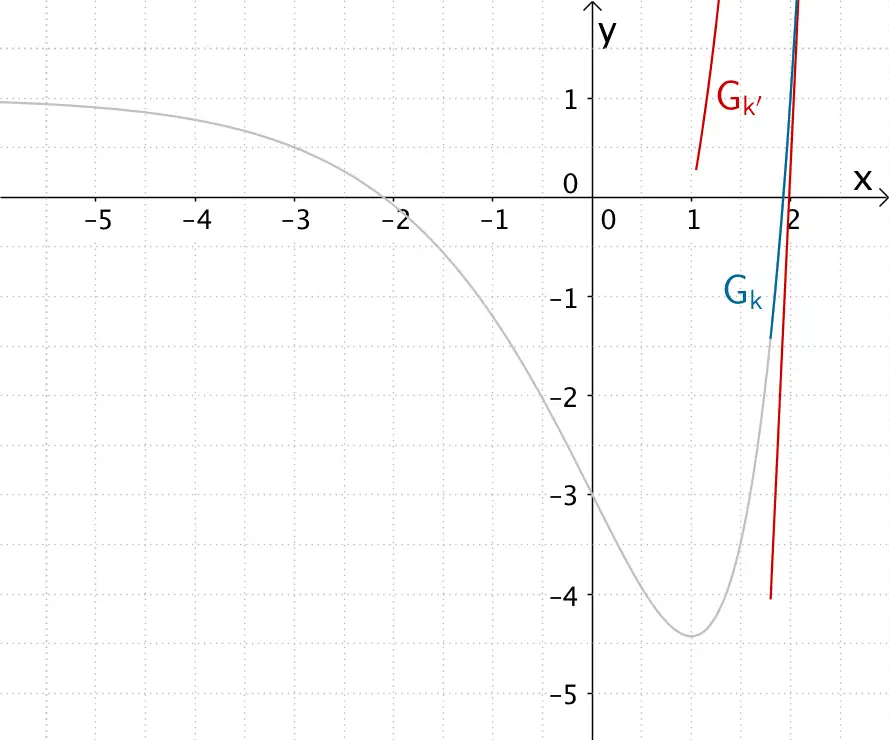
Für \(x > 1\) ist der Graph der Funktion \(k\) streng monoton steigend und strebt schnell gegen \(+\infty\). Der Wert der Steigung der Tangente an den Graphen der Funktion \(k\) strebt demnach für \(x > 1\) ebenfalls schnell gegen \(+\infty\).
Folglich verläuft der Graph der Ableitungsfunktion \(k'\) für \(x > 1\) oberhalb der \(x\)-Achse und strebt schnell gegen \(+\infty\).
Zusammenfassung der Ergebnisse
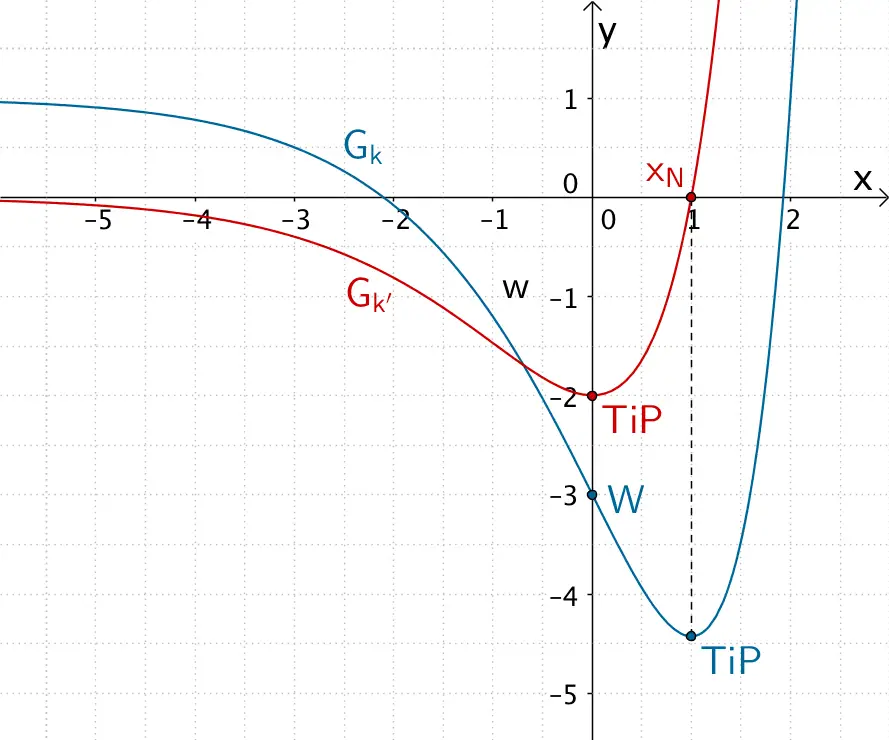
Graph der Funktion \(k\) und Graph der Ableitungsfunktion \(k'\)


