Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \frac{1}{100} \cdot \left( 2x^3 - 43x^2 + 248x \right)\). Abbildung 1 zeigt den Graphen \(G_f\) von \(f\) im Bereich \(0 \leq x \leq 10\).
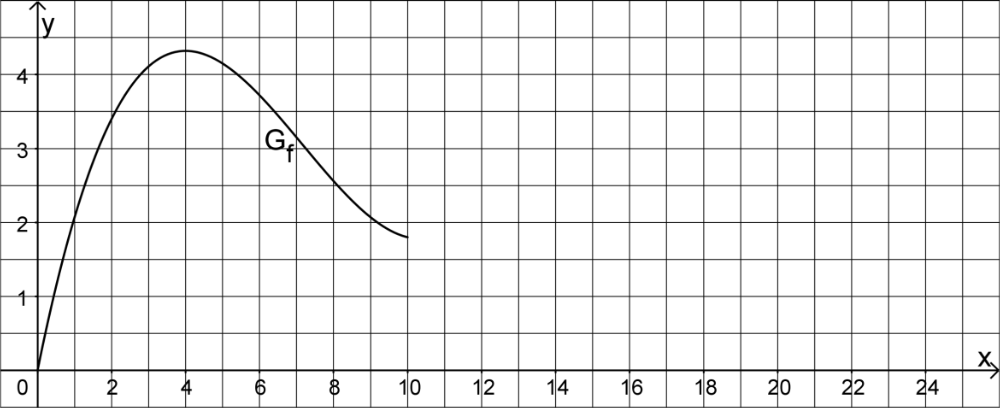Abb. 1
Begründen Sie anhand des Terms von \(f\), dass \(G_f\) nicht symmetrisch bezüglich des Koordinatenursprungs ist, und zeigen Sie rechnerisch, dass \(G_f\) für \(x < 7\frac{1}{6}\) rechtsgekrümmt ist.
(4 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = \frac{1}{100}\left(2x^3 - 43x^2 + 248x\right); \; D_f = \mathbb R\]
Begründung, dass \(G_f\) nicht symmetrisch bezüglich des Koordinatenursprungs ist
Da der Funktionsterm von \(f\) nicht ausschließlich Potenzen von \(x\) mit ungeradem Exponenten enthält, ist \(G_f\) nicht symmetrisch bezüglich des Koordinatenursprungs.
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.1.1 Ganzrationale Funktion - Symmetrie von Funktionsgraphen)
Rechnerischer Nachweis, dass \(G_f\) für \(x < 7\frac{1}{6}\) rechtsgekrümmt ist
Mithilfe der zweiten Ableitung \(f''\) lässt sich das Krümmungsverhalten des Graphen von \(f\) untersuchen.
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[f'(x) = \frac{1}{100}\cdot \left( 6x^2 - 86x + 248 \right)\]
\[f''(x) = \frac{1}{100} \cdot (12x - 86)\]
\(G_f\) ist in dem Bereich rechtsgekrümmt, für den \(f''(x) \textcolor{#cc071e}{<} 0\) gilt.
Anwendung der Differentialrechnung
Krümmungsverhalten von Funktionsgraphen
Der Graph einer in einem Intervall \(I = ]a;b[\) zweimal differenzierbaren Funktion \(f\) ist in \(I\)
linksgekrümmt \(\Large{\textcolor{#0087c1}{\curvearrowright}}\), wenn \(f''(x) \textcolor{#0087c1}{\boldsymbol{>}} 0\) ist für alle \(x \in I\)
positiv
rechtsgekrümmt \(\Large{\textcolor{#cc071e}{\curvearrowright}}\), wenn \(f''(x) \textcolor{#cc071e}{\boldsymbol{<}} 0\) ist für alle \(x \in I\)
negativ
\[\begin{align*} f''(x) &\textcolor{#cc071e}{<} 0 \\[0.8em] \Rightarrow \; 12x - 86 &< 0 &&| + 86 \\[0.8em] 12x &< 86 &&| : 12 \\[0.8em] x &< \frac{86}{12} \\[0.8em] x &< 7\frac{1}{6} \end{align*}\]
Somit ist \(G_f\) für \(x < 7\frac{1}{6}\) rechtsgekrümmt.
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.2.5 Krümmungsverhalten, Wendestellen und Wendepunkte)
