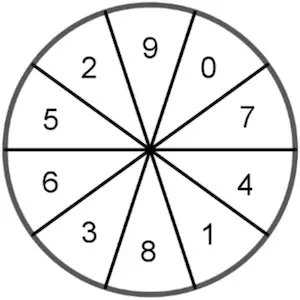
Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von 0 bis 9 durchnummeriert.
Das Glücksrad wird zwanzigmal gedreht. Bestimmen Sie die Wahrscheinlichkeit der Ereignisse \(A\) und \(B\).
\(A\): „Es wird genau siebenmal eine ungerade Zahl erzielt."
\(B\): „Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt."
(3 BE)
Lösung zu Teilaufgabe 1
\[\begin{align*} P(A) &= P_{0{}5}^{20}(X = 7) \\[0.8em] &= B(20;0{,}5;7) \\[0.8em] &= \binom{20}{7} \cdot 0{,}5^7 \cdot 0{,}5^{13} &&(\text{oder Tafelwerk}) \\[0.8em] &= 0{,}07393 \approx 7{,}4\,\%\end{align*}\]
\[\begin{align*}P(B) &= P_{0{,}5}^{20}(8 \leq X \leq 12) = P_{0{,}5}^{20}(X \leq 12) - P_{0{,}5}^{20}(X \leq 7) \\[0.8em] &= \sum \limits_{i\,=\,0}^{k \,=\,12}B(20;0{,}5;i) - \sum \limits_{i\,=\,0}^{k\,=\,7}B(20;0{,}5;i) \\[0.8em] &= 0{,}86841 - 0{,}13159 \\[0.8em] &= 0{,}73682 \approx 73{,}7\,\% \end{align*}\]
Ausführliche Erklärung (nicht verlangt)
Da nur zwischen den beiden sich gegenseitig ausschließenden Ereignissen „ungerade Zahl" und „nicht ungerade Zahl" unterschieden wird, beschreibt eine Drehung des Glücksrads ein Bernoulli-Experiment. 20 Drehungen des Glücksrads bilden eine Bernoulli-Kette der Länge \(\textcolor{#0087c1}{n = 20}\). Die Trefferwahrscheinlichkeit \(\textcolor{#cc071e}{p}\) für das Ereignis „ungerade Zahl" ist bei jeder Drehung konstant.
Bernoulli-Experiment, Bernoulli-Kette
Ein Zufallsexperiment, bei dem nur zwei verschiedene sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können, heißt Bernoulli-Experiment.
Das Eintreten des Ereignisses \(A\) wird als Treffer und das Eintreten des Gegeneignisses \(\overline{A}\) wird als Niete bezeichnet. Die Trefferwahrscheinlichkeit \(P(A)\) bezeichnet man mit \(\boldsymbol{p}\) und die Wahrscheinlichkeit für eine Niete mit \(q = 1- p\). Wird ein Bernoulli-Experiment \(n\)-mal wiederholt, spricht man von einer Bernoulli-Kette der Länge \(\boldsymbol{n}\). Dabei müssen die einzelnen Wiederholungen unabhängig voneinander erfolgen. Das heißt, die Trefferwahrscheinlichkeit \(p\) bleibt konstant.
Da die Sektoren des Glücksrads gleich groß sind, sind alle Ergebnisse \(\Omega = \{0;1;2;3;4;5;6;7;8;9\}\) gleichwahrscheinlich (Laplace-Experiment).
Das Glücksrad zeigt 5 ungerade Zahlen \(\{1;3;5;7;9\}\) von insgesamt 10 Zahlen. Die Laplace-Wahrscheinlichkeit für das Ereignis „ungerade Zahl" beträgt dann:
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
\[\textcolor{#cc071e}{p} = P(\text{„ungerade Zahl"}) = \frac{5}{10} \textcolor{#cc071e}{= 0{,}5}\]
Es sei \(X\) die Zufallsgröße, welche die Anzahl der erzielten ungeraden Zahlen von 20 Drehungen beschreibt.
Die Zufallsgröße \(X\) ist nach \(B(\textcolor{#0087c1}{20};\textcolor{#cc071e}{0{,}5})\) binomialverteilt.
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Wahrscheinlichkeit des Ereignisse \(A\)
\(A\): „Es wird genau siebenmal eine ungerade Zahl erzielt."
\[\begin{align*} P(A) &= P_{\textcolor{#cc071e}{0{}5}}^{\textcolor{#0087c1}{20}}(\textcolor{#e9b509}{X = 7}) \\[0.8em] &= B(\textcolor{#0087c1}{20};\textcolor{#cc071e}{0{,}5};\textcolor{#e9b509}{7}) \\[0.8em] &= \binom{\textcolor{#0087c1}{20}}{\textcolor{#e9b509}{7}} \cdot \textcolor{#cc071e}{0{,}5}^{\textcolor{#e9b509}{7}} \cdot (1 - \textcolor{#cc071e}{0{,}5})^{\textcolor{#0087c1}{20} \,-\,\textcolor{#e9b509}{7}} &&(\text{oder Tafelwerk, linke Spalte}) \\[0.8em] &= 0{,}07393 \approx 7{,}4\,\%\end{align*}\]
Wahrscheinlichkeit des Ereignisse \(B\)
\(B\): „Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt."
gleichbedeutend mit
\(B\): „Es wird mindestens achtmal und höchstens zwölfmal eine ungerade Zahl erzielt."
Stochastisches Tafelwerk verwenden:
Durch geeignete Differenzbildung lässt sich die Berechnung auf die kumulative Verteilungsfunktion (von \(0\) bis \(k\) aufsummierte Einzelwahrscheinlichkeiten) zurückführen. Diese ist im Stochastische Tafelwerk (ST) in der rechten Spalte tabellarisiert.
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\[\begin{align*}P(B) &= P_{\textcolor{#cc071e}{0{,}5}}^{\textcolor{#0087c1}{20}}(\textcolor{#e9b509}{7 < X \leq 12}) &&\textcolor{#e9b509}{\text{„mehr als siebenmal und höchstens zwölfmal"}} \\[0.8em] &= P_{\textcolor{#cc071e}{0{,}5}}^{\textcolor{#0087c1}{20}}(\textcolor{#e9b509}{8 \leq X \leq 12}) &&\textcolor{#e9b509}{\text{„mindestens achtmal und höchstens zwölfmal"}} \\[0.8em] &= P_{\textcolor{#cc071e}{0{,}5}}^{\textcolor{#0087c1}{20}}(\textcolor{#e9b509}{X \leq 12}) - P_{\textcolor{#cc071e}{0{,}5}}^{\textcolor{#0087c1}{20}}(\textcolor{#e9b509}{X \leq 7}) &&\textcolor{#e9b509}{\text{„höchstens zwölfmal"}}\;\text{minus}\;\textcolor{#e9b509}{\text{„höchstens siebenmal"}} \\[0.8em] &= \sum \limits_{\textcolor{#e9b509}{i\,=\,0}}^{\textcolor{#e9b509}{k \,=\,12}}B(\textcolor{#0087c1}{20};\textcolor{#cc071e}{0{,}5};i) - \sum \limits_{\textcolor{#e9b509}{i\,=\,0}}^{\textcolor{#e9b509}{k\,=\,7}}B(\textcolor{#0087c1}{20};\textcolor{#cc071e}{0{,}5};i) &&\text{jeweils Tafelwerk, rechte Spalte} \; \\[0.8em] &\overset{\text{ST}}{=} 0{,}86841 - 0{,}13159 \\[0.8em] &= 0{,}73682 \approx 73{,}7\,\% \end{align*}\]

