Gegeben sind die in \(\mathbb R\) definierten Funktionen \(g_{a,c} \, \colon x \mapsto \sin (ax) + c\) mit \(a,c \in \mathbb R^+_0\).
Geben Sie für jede der beiden folgenden Eigenschaften einen möglichen Wert für \(a\) und einen möglichen Wert für \(c\) so an, dass die zugehörige Funktion \(g_{a,c}\) diese Eigenschaft besitzt.
α) Die Funktion\(g_{a,c}\) hat die Wertemenge \([0;2]\).
β) Die Funktion \(g_{a,c}\) hat im Intervall \([0;\pi]\) genau drei Nullstellen.
(3 BE)
Lösung zu Teilaufgabe 3a
\[g_{a,c}(x) = \sin(ax) + c\,; \quad a,c \in \mathbb R_0^+\]
Im Falle der gegebenen Funktion \(g_{a,c}\) streckt oder staucht der Parameter \(a\) den Graphen \(G_{g_{a,c}}\) in \(x\)-Richtung und verschiebt der Parameter \(c\) den Graphen \(G_{g_{a,c}}\) in \(y\)-Richtung.
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
α) Die Funktion \(g_{a,c}\) hat die Wertemenge \([0;2]\).
Der Wert des Parameters \(a\) wirkt sich nicht auf die Wertemenge der Funktion \(g_{a,c}\) aus. Er kann beliebig gewählt werden, z.B. \(a=1\).
Der Graph der Funktion \(g_{a,c}\) mit der Wertemenge \(W = [0;2]\) ist gegenüber dem Graphen der Sinusfunktion \(x \mapsto \sin x\) mit der Wertemenge \(W =[-1;1]\) um \(c = 1\) in \(y\)-Richtung verschoben.
\(\Longrightarrow \quad g_{1,1}(x) = \sin x + 1\)
Die Funktion \(g_{1,1}\) hat die Wertemenge \(W = [0;2]\).
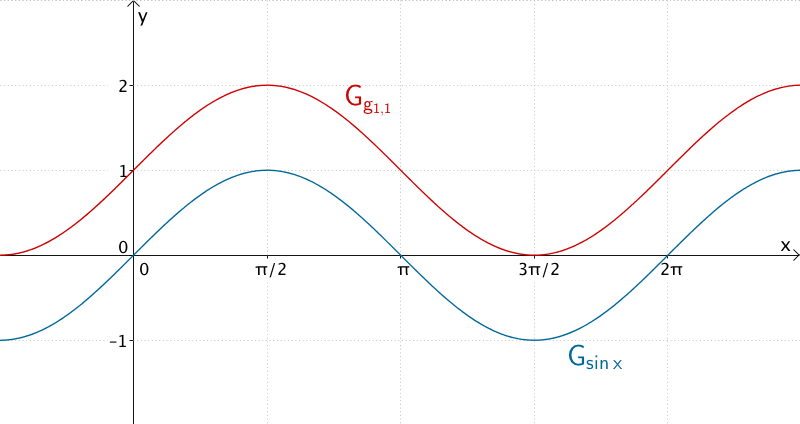
Graph der Funktion \(g_{1,1}\) und Graph der Sinusfunktion \(x \mapsto \sin x\)
β) Die Funktion \(g_{a,c}\) hat im Intervall \([0;\pi]\) genau drei Nullstellen.
Die Sinusfunktion \(x \mapsto \sin x\) besitzt mit \(x_1 = 0\), \(x_2 = \pi\) und \(x_3 = 2\pi\) bei einer Periodenlänge \(p = 2\pi\) im Intervall \([0;2\pi]\) genau drei Nullstellen.
Damit die gesuchte Funktion \(g_{a,c}\) im Intervall \([0;\pi]\) genau drei Nullstellen hat, muss für deren Periodenlänge \(p = \pi\) gelten. Das bedeutet, dass der Graph der Funktion \(g_{a,c}\) gegenüber dem Graphen der Funktion \(x \mapsto \sin x\) um den Faktor 2 gestaucht bzw. um den Faktor 0,5 gestreckt sein muss. Mit \(\displaystyle p = \frac{2\pi}{a}\) folgt:
Allgemeine Sinusfunktion
\[f(x) = a \cdot \sin(bx + c) + d = a \cdot \sin \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
\[\begin{align*} \pi &= \frac{2\pi}{a} & &| \; \cdot a \quad : \pi \\[0.8em] a &= \frac{2\pi}{\pi} = 2 \end{align*}\]
\[\Longrightarrow \quad g_{2,c}(x) = \sin(2x) + c\]
Eine Verschiebung des Graphen der Funktion \(g_{2,c}\) in \(y\)-Richtung würde die Anzahl der Nullstellen im Intervall \([0;\pi]\) verringern.
\[\Longrightarrow \quad c = 0\]
\[\Longrightarrow \quad g_{2,0}(x)= \sin(2x)\]
Die Funktion \(g_{2,0}\) besitzt mit \(x_1 = 0\), \(\displaystyle x_2 = \frac{\pi}{2}\) und \(x_3 = \pi\) bei einer Periodenlänge \(p = \pi\) im Intervall \([0;\pi]\) genau drei Nullstellen.
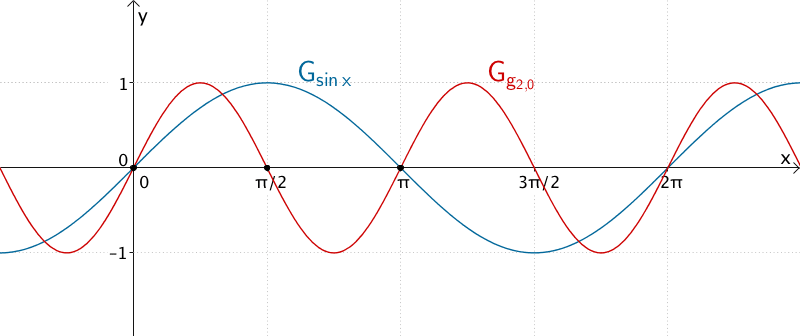
Graph der Funktion \(g_{2,0}\) und Graph der Sinusfunktion \(x \mapsto \sin x\)


