Bestimmen Sie die Wahrscheinlichkeit dafür, dass keine Person mit Reservierung abgewiesen werden muss.

(3 BE)

Lösung zu Teilaufgabe 2b

$p=0,1$, $n=64$

$X$: Anzahl der Personen mit Reservierung, die nicht zur Fahrt erscheinen.

$X$ ist nach $B(64;0,1)$ binomialverteilt.

Tabelle der Angabe:

Binomialverteilung kumulativ; $k\mapsto \sum _{i=0}^{k}B(n;p;i)$

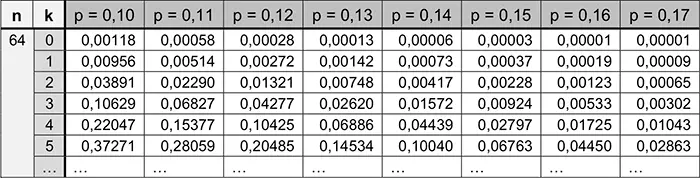
Wenn von 64 Personen mindestens 4 Personen mit Reservierung nicht erscheinen, muss keine Person mit Reservierung abgewiesen werden.

$$\begin{array}{rl}{P}_{0,1}^{64}(X\ge 4)& =1-P_{0,1}^{64}(X\le 3)\\ & =1-\sum _{I=0}^{k=3}B(64;0,1;i)& & |n=64;\text{Tabelle der Angabe verwenden}\\ & \stackrel{\text{Tabelle}}{=}1-\mathrm{0,106}29\\ & =\mathrm{0,893}71\\ & \approx 89,4\mathrm{\%}\end{array}$$