Gegeben sind die beiden Kugeln \(k_{1}\) mit Mittelpunkt \(M_{1}(1|2|3)\) und Radius \(5\) sowie \(k_{2}\) mit Mittelpunkt \(M_{2}(-3|-2|1)\) und Radius \(5\).
Zeigen Sie, dass sich \(k_{1}\) und \(k_{2}\) schneiden.
(2 BE)
Lösung zu Teilaufgabe 1a
\[k_{1} \colon M_{1}(1|2|3); \; r_{1} = 5\]
\[k_{2} \colon M_{2}(-3|-2|1); \; r_{2} = 5\]
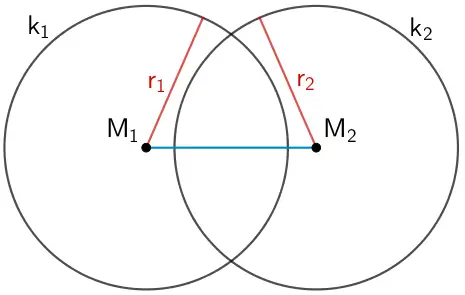
Die Kugeln \(k_{1}\) und \(k_{2}\) schneiden sich, wenn der Abstand \(\textcolor{#0087c1}{d(M_{1};M_{2}) = \overline{M_{1}M_{2}}}\) kleiner ist als die Summe der Radien \(\textcolor{#cc071e}{r_{1}}\) und \(\textcolor{#cc071e}{r_{2}}\)
Bedingung \(\textcolor{#0087c1}{\overline{M_{1}M_{2}}} < \textcolor{#cc071e}{r_{1} + r_{2}}\) nachweisen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \textcolor{#0087c1}{\overline{M_{1}M_{2}}} &= \vert \overline{M_{1}M_{2}} \vert \\[0.8em] &= \vert \overline{M_{2}} - \overline{M_{1}} \vert \\[0.8em] &= \left| \begin{pmatrix} -3 \\ -2 \\ 1 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -4 \\ -4 \\ -2 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-4)^{2} + (-4)^{2} + (-2)^{2}} \\[0.8em] &= \sqrt{36} \\[0.8em] &= \textcolor{#0087c1}{6} \end{align*}\]
\[\textcolor{#cc071e}{r_{1} + r_{2}} = 5 + 5 = \textcolor{#cc071e}{10}\]
\[\textcolor{#0087c1}{6} < \textcolor{#cc071e}{10}\]
Also schneiden sich die Kugeln \(k_{1}\) und \(k_{2}\).


