Eine in \(\mathbb R\) definierte ganzrationale Funktion \(g\) hat die folgenden Eigenschaften:
- \(t\) ist Tangente an den Graphen von \(g\) im Punkt \(\big(\frac{9}{4} \big| 0\big)\).
- Der Graph von \(g\) verläuft für \(0 < x < \frac{9}{4}\) oberhalb von \(t\).
Geben Sie einen möglichen Term von \(g\) an.
(3 BE)
Lösung zu Teilaufgabe 1d
Eine ganzrationale Funktion vom Grad 1 (lineare Funktion) kommt für \(g\) nicht infrage, da deren Gerade mit der Tangente \(t\) identisch sein müsste und für \(0 < x < \frac{9}{4}\) nicht oberhalb von \(t\) verlaufen könnte.
Eine ganzrationale Funktion vom Grad 2 (quadratische Funktion) ist ein überschaubarer Ansatz, der graphisch plausibel erscheint. Die zugehörige Parabel muss durch den Punkt \(\big(\frac{9}{4} \big| 0\big)\) verlaufen und dort die Steigung der Tangente \(t\) haben.
Die genannten Eigenschaften liefern die Gleichungen \(g\Big( \frac{9}{4}\Big) = 0\) und \(g'\Big( \frac{9}{4}\Big) = -\frac{3}{2}\) (Steigung der Tangente \(t\), vgl. Teilaufgabe 1c). Diese reichen nicht aus, um damit eine quadratische Funktion \(g\) der Form \(g(x) = ax^2 + bx + c\) zu bestimmen. Der Operator „Geben Sie an" verweist ohnehin auf eine Lösung ohne Rechenaufwand.
Addiert man zum Term der Tangente \(t\colon y = -\frac{3}{2}x + \frac{27}{8}\) einen quadratischen Term, der die Nullstelle \(x = \frac{9}{4}\) besitzt und dessen Wert stets positiv ist, also beispielsweise \(\big( x - \frac{9}{4}\big)^2\), entsteht eine quadratische Funktion, die die vorgegebenen Eigenschaften erfüllt.
Möglicher Term: \(g(x) = \textcolor{#cc071e}{-\dfrac{3}{2}x + \dfrac{27}{8}} + \underbrace{\left( x - \dfrac{9}{4} \right)^2}_{>\,0}\)
Durch die Addition zweier Funktionsterme mit jeweils der Nullstelle \(x = \frac{9}{4}\) bleibt die Nullstelle erhalten.
\[g'(x) = -\frac{3}{2} + 2 \cdot \left( x - \frac{9}{4} \right)\]
\[g'\left( \frac{9}{4} \right) = -\frac{3}{2}\]
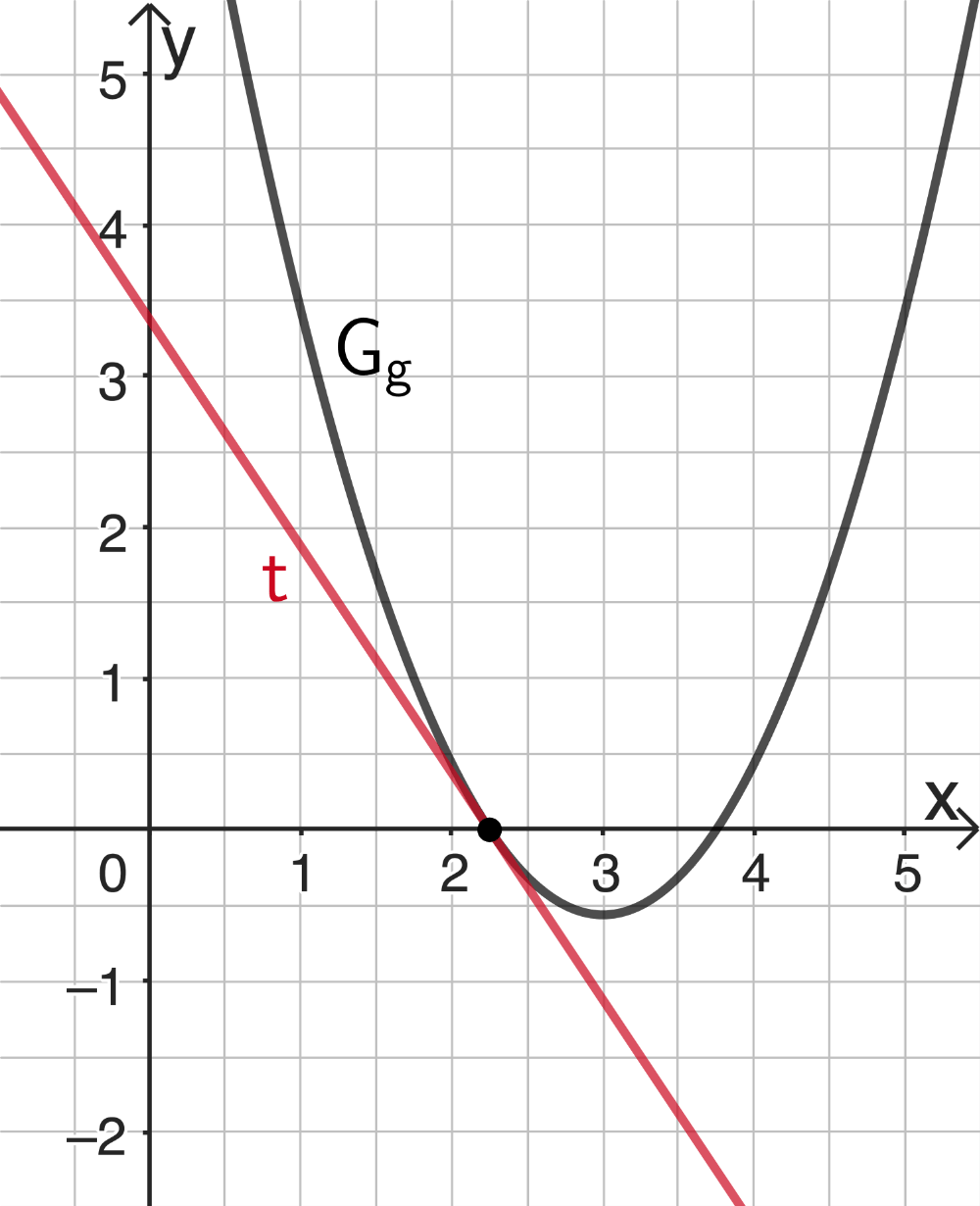
Tangente \(\textcolor{#cc071e}{t}\) und Graph von \(g\)


