Zwei Punkte \(U\) und \(V\) der Geraden \(h\) bilden zusammen mit \(P\) und \(Q\) das Rechteck \(PUQV\). Beschreiben Sie einen Weg zur Ermittlung der Koordinaten von \(U\) und \(V\).
(4 BE)
Lösung zu Teilaufgabe 2c
1. Lösungsansatz: Länge eines Vektors, Einheitsvektor
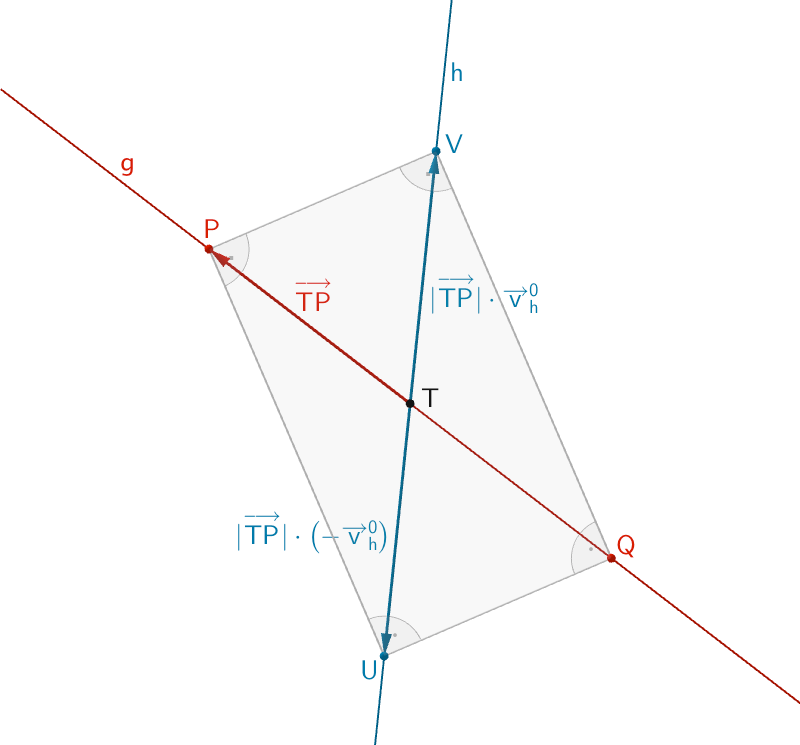
Da die Längen der Diagonalen eines Rechtecks gleich lang sind, können die Vektoren \(\overrightarrow{TU}\) und \(\overrightarrow{TV}\) als Produkt des Einheitsvektors \(\overrightarrow{v}^0_h\) der Geraden \(h\) bzw. dessen Gegenvektor und der Länge des Vektors \(\overrightarrow{TP}\) beschrieben werden.
A) Länge des Vektors \(TP\) bestimmen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{TP} = \vert \overrightarrow{TP} \vert\]
B) Einheitsvektor des Richtungsvektors der Geraden \(h\) bestimmen:
Einheitsvektor (vgl. Merkhilfe)
\[\overrightarrow{a}^0 = \frac{\overrightarrow{a}}{\vert \overrightarrow{a} \vert}\]
Vektoren mit der Länge 1 heißen Einheitsvektoren.
\[\overrightarrow{v}^0_h = \frac{\overrightarrow{v}_h}{\vert \overrightarrow{v}_h \vert}\]
C) Koordinaten der Punkte \(U\) und \(V\) bestimmen:
Hierbei ist zu beachten, dass die Benennung der Eckpukte gegen den Uhrzeigersinn erfolgt.
\[\overrightarrow{U} = \overrightarrow{T} + \vert \overrightarrow{TP} \vert \cdot \left( -\overrightarrow{v}^0_h \right)\]
\[\overrightarrow{V} = \overrightarrow{T} + \vert \overrightarrow{TP} \vert \cdot \overrightarrow{v}^0_h\]
2. Lösungsansatz: Anwenden des Skalarprodukts (Orthogonale Vektoren)
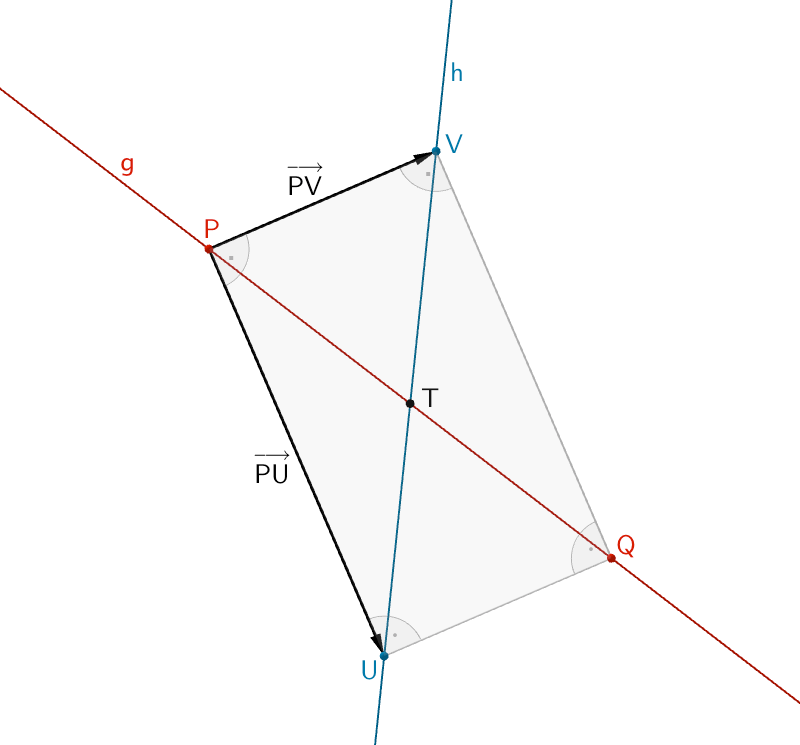
Die Vektoren \(\overrightarrow{PU}\) und \(\overrightarrow{PV}\) mit \(U\,,V \in h\) stehen senkrecht zueinander.
A) Anwenden des Skalarprodukts: Orthogonale Vektoren
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{PU} \perp \overrightarrow{PV} \quad \Longleftrightarrow \quad \overrightarrow{PU} \circ \overrightarrow{PV} \overset{!}{=} 0\]
\[U\,, V \in h \quad \Longrightarrow \quad \overrightarrow{PU}(\mu) \circ \overrightarrow{PV}(\mu) \overset{!}{=} 0\]
B) Parameter \(\mu\) berechnen:
Der Ansatz \(\overrightarrow{PU}(\mu) \circ \overrightarrow{PV}(\mu) = 0\) ergibt einen quadratische Gleichung mit den Lösungen \(\mu_{1,2}\).
C) Koordinaten der Punkte \(U\) und \(V\) bestimmen:
\[U\,, V \in h\]
Parameterwerte für \(\mu_{1,2}\) in die Geradengleichung von \(h\) einsetzen. Die Benennung der Eckpunkte des Rechtecks \(PUQV\) erfolgt gegen den Uhrzeigersinn.
3. Lösungsansatz: Schnittpunkte einer Geraden mit einer Kugel
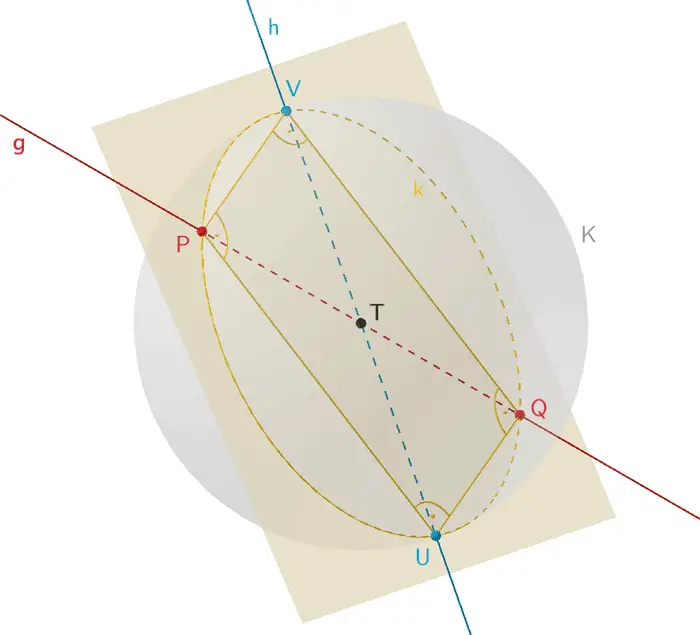
Die Geraden \(g\) und \(h\) legen eine Ebene fest, in der das Rechteck \(PUQV\) liegt. Schneidet man eine Kugel \(K\) mit dem Mittelpunkt \(T\) und dem Durchmesser \(d = \overline{PQ}\) mit dieser Ebene, ist der entstehende Schnittkreis \(k\) der Umkreis des Rechtecks \(PUQV\). Die Punkte \(U\) und \(V\) liegen auf dem Schnittkreis \(k\) und somit auf der Kugeloberfläche. Folglich lassen sich die Koordinaten der Punkte \(U\) und \(V\) als Schnittpunkte der Geraden \(h\) mit der Kugel \(K\) bestimmen.
A) Kugelgleichung aufstellen:
\[T\,(2|-1|3)\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{TP} = \vert \overrightarrow{TP} \vert\]
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[K\,\colon\; (x_1 - 2)^2 + (x_2 + 1)^2 + (x_3 - 3)^2 = {\overline{TP}}^2\]
B) Parameter \(\mu\) berechnen:
\[h\,\colon\; \overrightarrow{X} = \begin{pmatrix} -1 \\ 5 \\ -9 \end{pmatrix} + \mu \cdot \begin{pmatrix} 1 \\ -2 \\ 4 \end{pmatrix}\,; \enspace \mu \in \mathbb R\]
\[h \cap K\]
Man erhält eine Quadratische Gleichung mit den Lösungen \(\mu_{1,2}\).
C) Koordinaten der Punkte \(U\) und \(V\) bestimmen:
\[U\,, V \in h\]
Parameterwerte für \(\mu_{1,2}\) in die Geradengleichung von \(h\) einsetzen. Die Benennung der Eckpunkte des Rechtecks \(PUQV\) erfolgt gegen den Uhrzeigersinn.


