Spiegelt man die Ebene \(T\) an \(U\), so erhält man die von \(T\) verschiedene Ebene \(T'\). Zeigen Sie, dass für einen bestimmten Wert von \(a\) die Gerade \(g_{a}\) in der Ebene \(T\) liegt, und begründen Sie, dass diese Gerade \(g_{a}\) die Schnittgerade von \(T\) und \(T'\) ist.
(4 BE)
Lösung zu Teilaufgabe e
Wert von \(a\), sodass die Gerade \(g_{a}\) in der Ebene \(T\) liegt
\(g_{a} \colon \overrightarrow{X} = \begin{pmatrix} 2{,}5 \\ 0 \\ 3{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -10a \\ \frac{2}{a} \end{pmatrix}; \;\lambda \in \mathbb R, \; a \in \mathbb R^{+}\) (vgl. Teilaufgabe c)
\(T \colon 5x_{1} + 4x_{2} + 5x_{3} - 30 = 0\) (vgl. Teilaufgabe b)
Die Gerade \(g_{a}\) liegt für einen bestimmten Wert von \(a\) in der Ebene T, wenn der Richtungsvektor von \(g_{a}\) und der Normalenvektor der Ebene \(T\) zueinander senkrecht sind. Das Skalarprodukt der Vektoren muss also gleich Null sein. Zudem muss der Aufpunkt von \(g_{a}\) in der Ebene \(T\) liegen.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\begin{align*} \begin{pmatrix} 0 \\ -10a \\ \frac{2}{a} \end{pmatrix} \circ \begin{pmatrix} 5 \\ 4 \\ 5 \end{pmatrix} &= 0 \\[0.8em] 0 \cdot 5 - 10a \cdot 4 + \frac{2}{a} \cdot 5 &= 0 \\[0.8em] -40a + \frac{10}{a} &= 0 &&| \cdot a \\[0.8em] -40a^{2} + 10 &= 0 &&| - 10 \\[0.8em] -40a^{2} &= -10 &&| : (-40) \\[0.8em] a^{2} &= 0{,}25 &&| \; \sqrt{\quad} \enspace a \in \mathbb R^{+} \\[0.8em] a &= 0{,}5 \end{align*}\]
Schlussfolgerung: Die Gerade \(g_{0{,}5}\) verläuft parallel zur Ebene \(T\)
Prüfen, ob der Aufpunkt \((2{,}5|0|3{,}5)\) von \(g_{a}\) in der Ebene \(T\) liegt (Punktprobe):
\[\begin{align*} (2{,}5|0|3{,}5) \in T \colon 5 \cdot 2{,}5 + 4 \cdot 0 + 5 \cdot 3{,}5 - 30 &= 0 \\[0.8em] 12{,}5 + 17{,}5 -30 &= 0 \\[0.8em] 30 - 30 &= 0 &&(\text{w}) \end{align*}\]
Schlussfolgerung: Die Gerade \(g_{0{,}5}\) liegt in der Ebene T \((g_{0{,}5} \subset T)\).
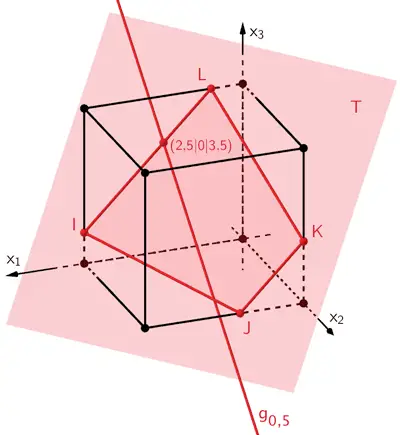
Gerade \(g_{0{,}5} \subset T\) (Zeichnung nicht verlangt)
Begründung, dass \(g_{0{,}5}\) die Schnittgerade von \(T\) und \(T'\) ist
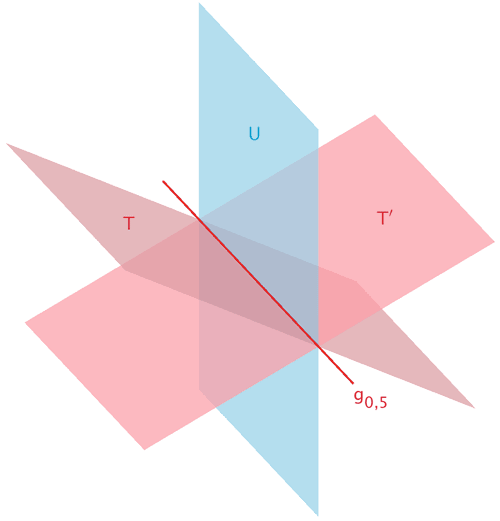
(Zeichnung schematisch und nicht verlangt)
\(g_{a} \colon \overrightarrow{X} = \begin{pmatrix} \textcolor{#0087c1}{2{,}5} \\ 0 \\ 3{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} \textcolor{#0087c1}{0} \\ -10a \\ \frac{2}{a} \end{pmatrix}; \;\lambda \in \mathbb R, \; a \in \mathbb R^{+}\) (vgl. Teilaufgabe c)
Da die \(\textcolor{#0087c1}{x_{1}}\)-Koordinate des Richtungsvektors von \(g_{a}\) gleich Null ist und die Gerade \(g_{a}\) durch den Punkt \((\textcolor{#0087c1}{2{,}5}|0|3{,}5)\) verläuft, liegt die Gerade \(g_{a}\) für jedes \(a \in \mathbb R^{+}\) in der Ebene \(\textcolor{#0087c1}{U \colon x_{1} = 2{,}5}\).
Somit liegt die Gerade \(g_{0{,}5}\) in der Ebene \(T\) und in der Ebene \(U\). Bei der Spiegelung der Ebene \(T\) an der Ebene \(U\) ist die Gerade \(g_{0{,}5}\) Fixgerade der Spiegelung und deshalb die Schnittgerade von \(T\) und \(T'\).


