Die Abbildung 1 zeigt den Graphen \(G_{f'}\) der Ableitungsfunktion \(f'\) einer in \(\mathbb R\) definierten ganzrationalen Funktion \(f\). Nur in den Punkten \((-4|f'(-4))\) und \((5|f'(5))\) hat der Graph \(G_{f'}\) waagrechte Tangenten.
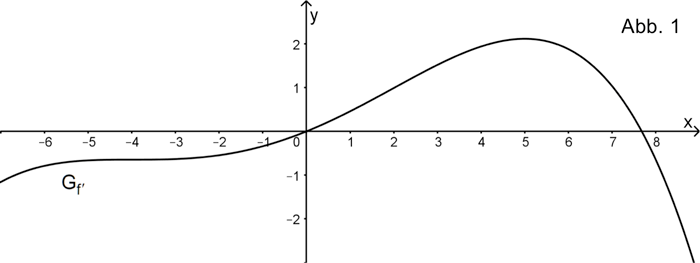
Begründen Sie, dass \(f\) genau eine Wendestelle besitzt.
(2 BE)
Lösung zu Teilaufgabe 2a
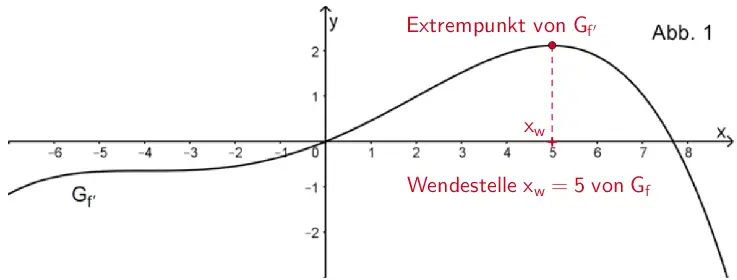
An einer Wendestelle ist die Steigung des Graphen einer Funktion extremal (minimal oder maximal). Da die erste Ableitung einer Funktion die Steigung des Graphen der Funktion beschreibt, hat der Graph der Ableitungsfunktion an der Wendestelle einen Extrempunkt.
Abbildung 1 zeigt nur an der Stelle \(x = 5\) einen Extrempunkt des Graphen von \(f'\). Somit besitzt der Graph von \(f\) genau eine Wendestelle (\(x_{w} = 5\)).
Alternative Begründung:
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
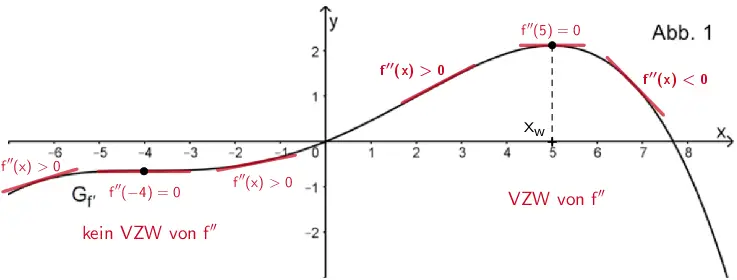
Die zweite Ableitung \(f''\) beschreibt die Steigung einer Tangente an den Graphen von \(f'\).
Nur an der Stelle \(x = 5\) gilt die notwendige Bedingung für einen Wendepunkt \(\textcolor{#cc071e}{f''(5) = 0}\) (waagrechte Tangente) und ein Vorzeichenwechsel (VZW) von \(\textcolor{#cc071e}{f''}\). Also ist \(x = 5\) einzige Wendestelle des Graphen von \(f\).

