Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(w_{a;b;c} \colon x \mapsto \dfrac{a}{b+e^{cx}}\) mit \(a,b \in \mathbb R^+\) und \(c \in \mathbb R\). Die Funktion aus Aufgabe 1 ist eine Funktion dieser Schar.
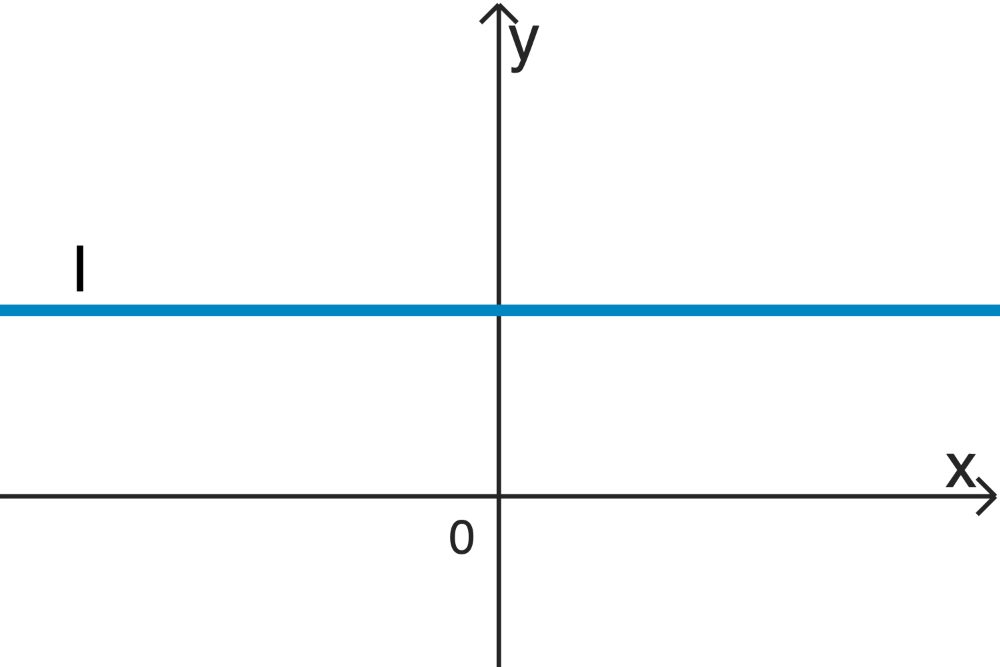
Jeder der abgebildeten Graphen I, II und III der Schar gehört, bei festen Werten von \(a\) und \(b\), zu einem der Werte \(c = -1\), \(c = 0\) und \(c = 1\).
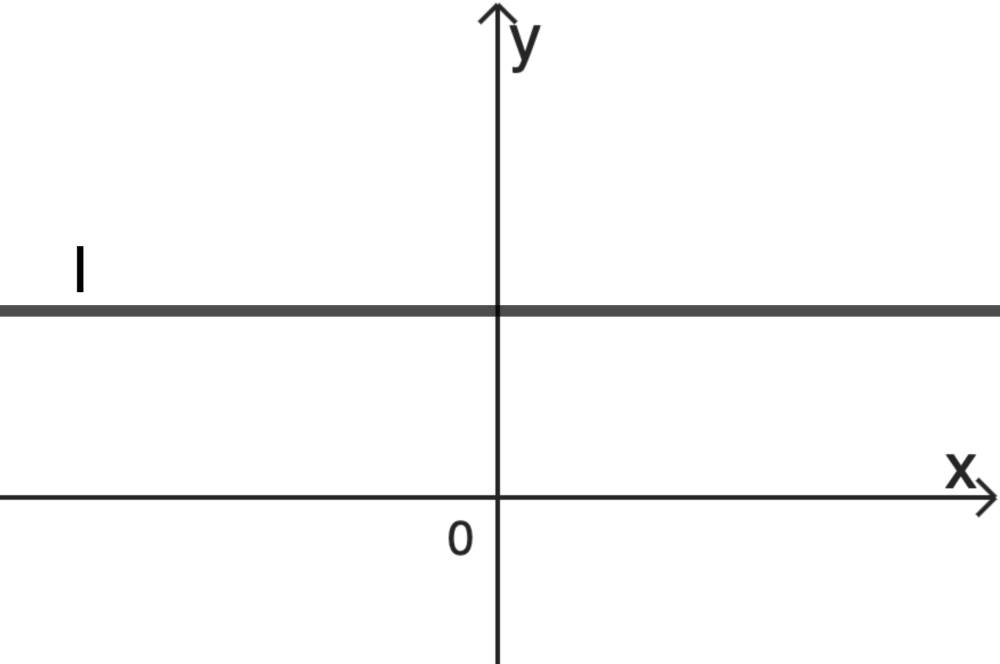
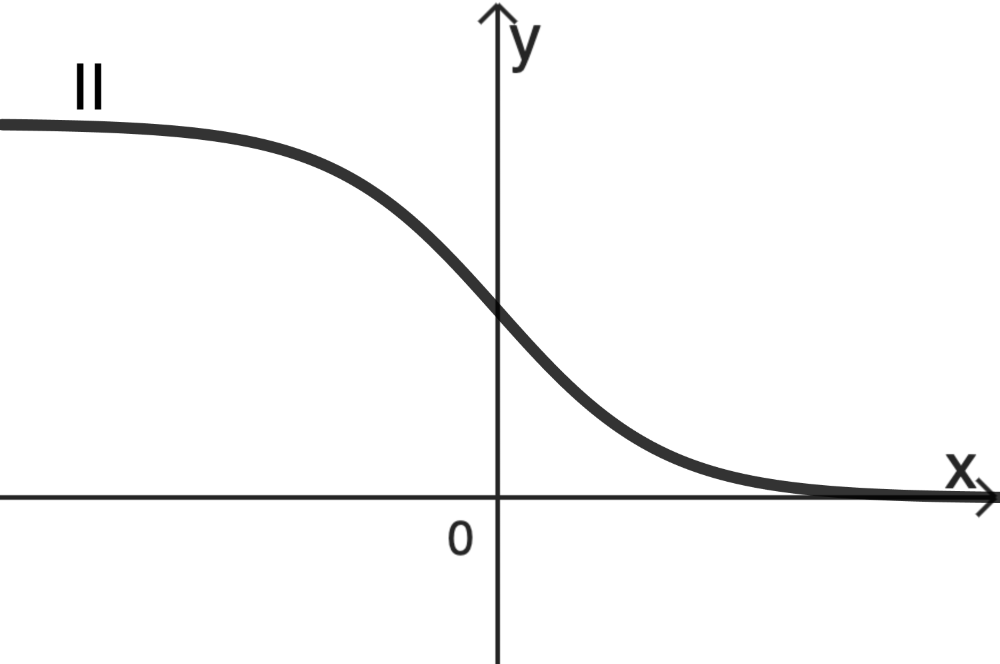
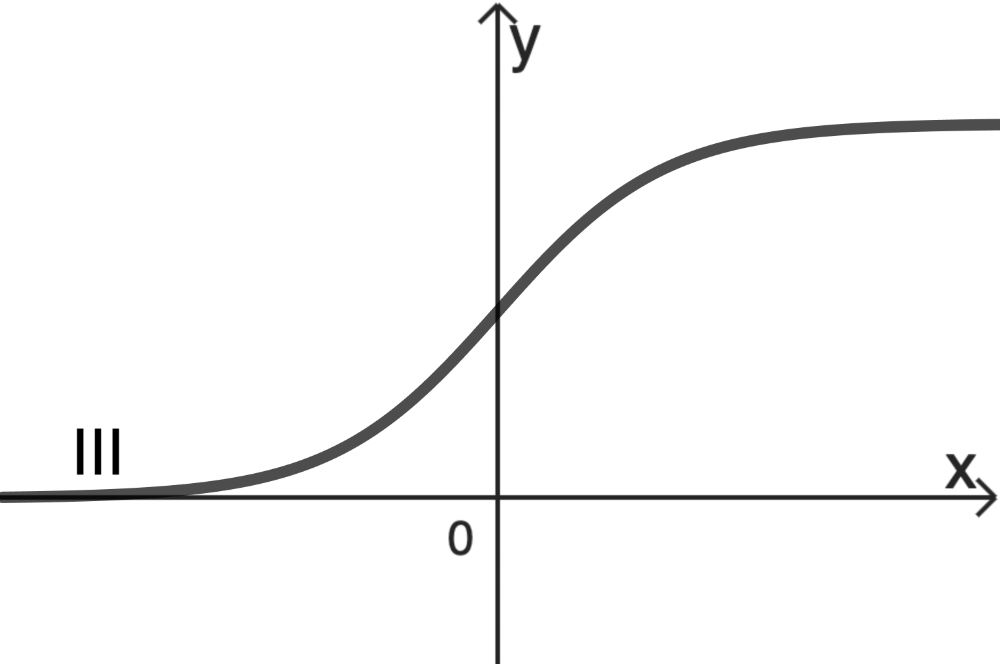
Ordne Sie den Graphen die genannten Werte von \(c\) zu und begründen Sie Ihre Zuordnung.
(4 BE)
Lösung zu Teilaufgabe 2a
\(c= 0\) gehört zu Graph I, da sich für \(c = \textcolor{#e9b509}{0}\) eine konstante Funktion der Form
\[w_{a;b;\textcolor{#e9b509}{0}}(x) = \frac{a}{b + e^{\textcolor{#e9b509}{0} \cdot x}} = \textcolor{#0087c1}{\frac{a}{b+1}}\]
ergibt.
Für \(c = 1\) gilt:
\[\lim \limits_{x\,\to\,+\infty} w_{a;b;1}(x) = \lim \limits_{x\,\to\,+\infty} \frac{a}{\textcolor{#cc071e}{\underbrace{b+e^x}_{\to\,+\infty}}} = \textcolor{#0087c1}{0}\]
Somit gehört \(c =1\) zu Graph II.
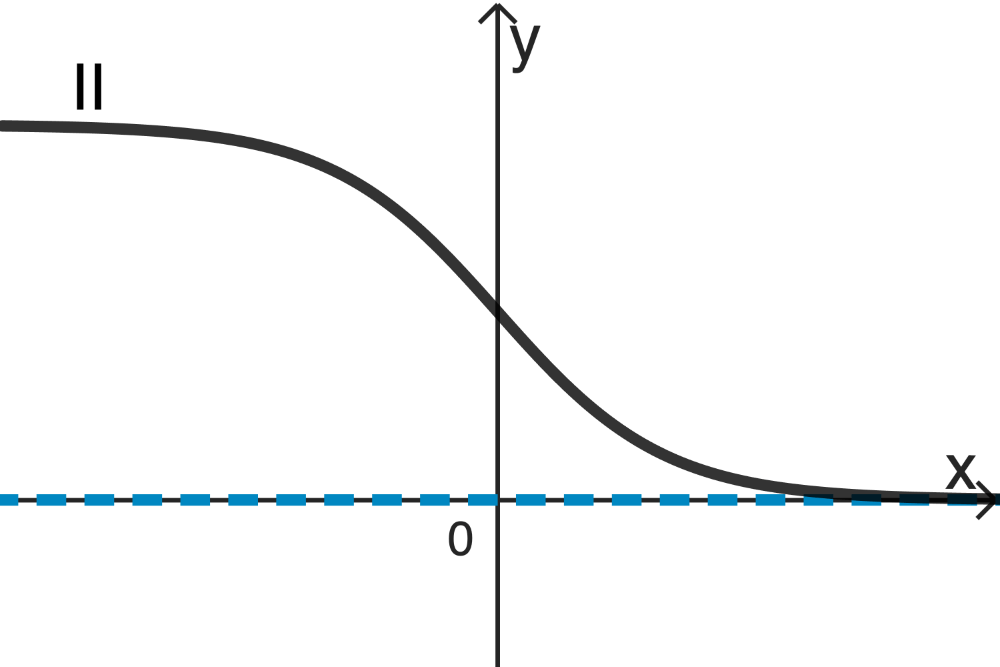
Nach dem Ausschlussprinzip gehört \(c = -1\) zu Graph III.
oder
Für \(c = -1\) gilt:
\[\lim \limits_{x\,\to\,+\infty} w_{a;b;-1}(x) = \lim \limits_{x\,\to\,+\infty} \frac{a}{\textcolor{#cc071e}{\underbrace{b+\underset{\to\,0}{e^{-x}}}_{\to\,b}}} = \textcolor{#0087c1}{\frac{a}{b}}\]
Somit gehört \(c =-1\) zu Graph III.