Abiturlösungen Mathematik Bayern 2016 Prüfungsteil A Stochastik 1
- Details
- Kategorie: Stochastik 1
Die beiden Baumdiagramme gehören zum selben Zufallsexperiment mit den Ereignissen \(A\) und \(B\).
Berechnen Sie die Wahrscheinlichkeit \(P(B)\) und ergänzen Sie anschließend an allen Ästen des rechten Baumdiagramms die zugehörigen Wahrscheinlichkeiten.
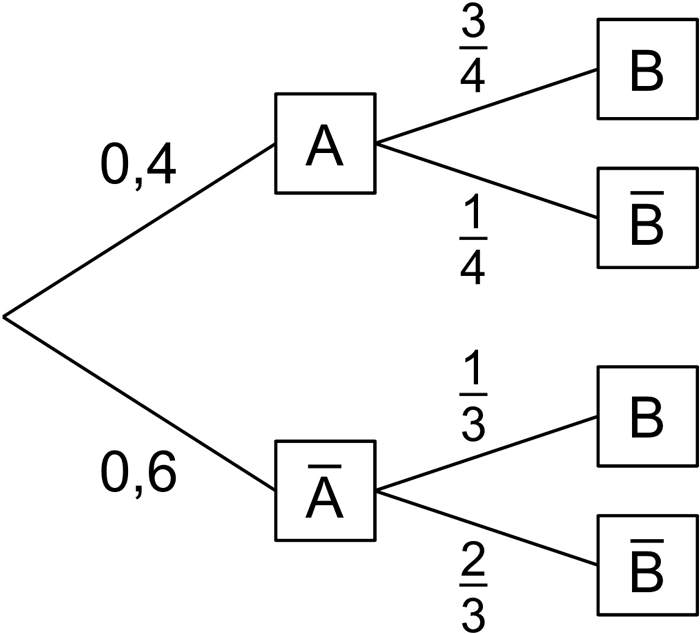
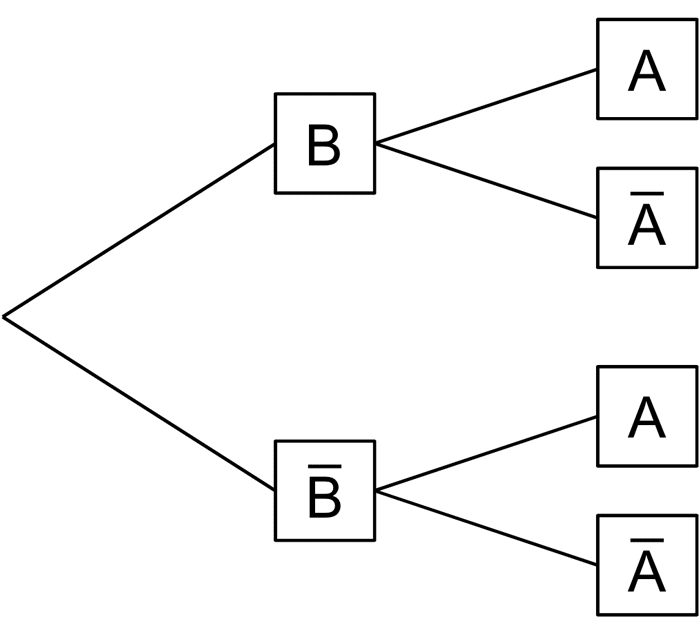
(Teilergebnis: \(P(B) = 0{,}5\))
(5 BE)
- Details
- Kategorie: Stochastik 1
Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl \((Z)\) oder zum zweiten Mal Wappen \((W)\) oben liegt. Als Ergebnismenge wird festgelegt: \(\{ZZ; WW; ZWZ; ZWW; WZZ; WZW\}\).
Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.
(2 BE)
- Details
- Kategorie: Stochastik 1
Die Zufallsgröße \(X\) ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von \(X\).
(3 BE)


