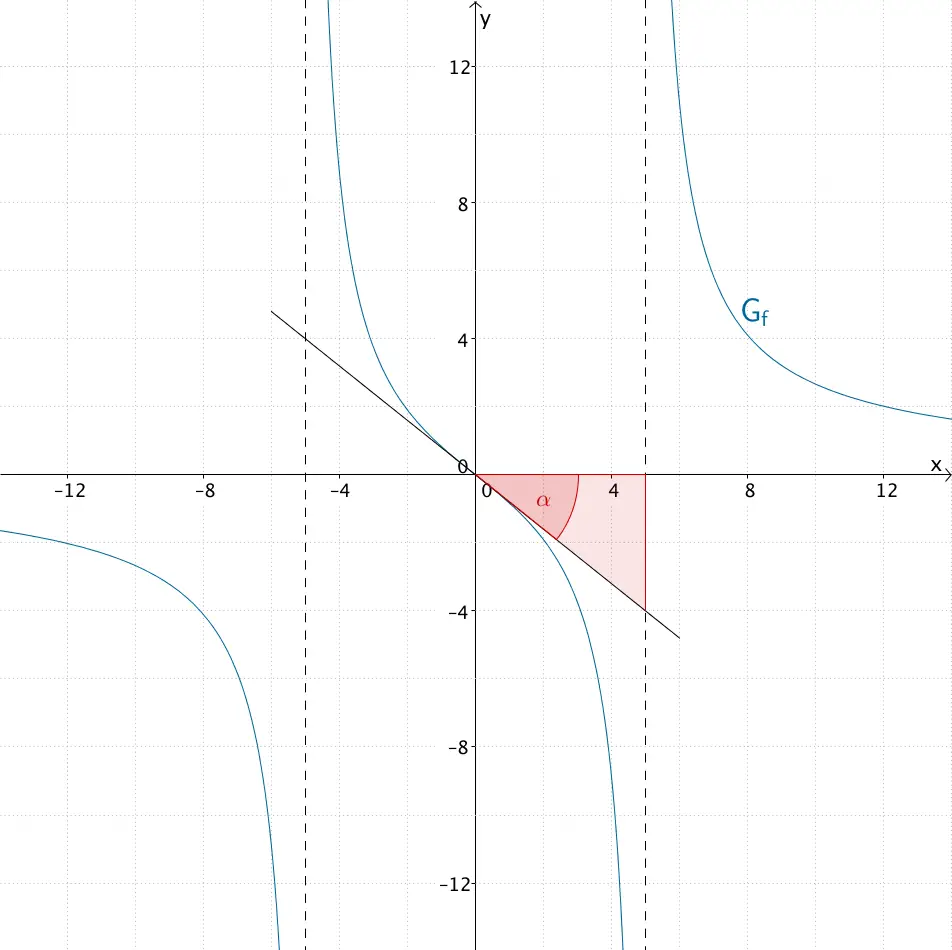
Skizzieren Sie in der Abbildung den darin fehlenden Teil von \(G_f\) unter Berücksichtigung der bisherigen Ergebnisse.
(3 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = \frac{20x}{x^2 - 25}\,; \quad D_{f} = \mathbb R \,\backslash\,\{-5;5\}\]
Bisherige Ergebnisse:
- Nullstelle: \(x = 0\)
- \(G_f\) ist punktsymmetrisch bezüglich des Koordinatenursprungs.
- Gleichungen der beiden senkrechte Asymptoten: \(x = -5\) und \(x = 5\)
- Gleichung der waagrechten Asymptote: \(y = 0\) (\(x\)-Achse)
- Die Steigung von \(G_f\) ist in jedem Punkt des Graphen negativ, d.h. \(G_f\) ist für alle \(x \in D_{f}\) streng monoton fallend.
- \(G_f\) schneidet die \(x\)-Achse (an der Nullstelle) unter dem Winkel \(\alpha = 38{,}66^{\circ}\).
Graph der Funktion \(f\)
Aufgrund der Punktsymmetrie von \(G_{f}\) lässt sich zunächst der für \(x > 5\) bereits gezeichnete Teil von \(G_f\) (siehe Abbildung zu Teilaufgabe 1) am Koordinatenursprung spiegeln. Anschließend zeichnet man die beiden senkrechten Asymptoten ein. Der Verlauf von \(G_{f}\) für \(-5 < x < 5\) muss von \(+\infty\) nach \(-\infty\) erfolgen, da \(G_{f}\) für alle \(x \in D_{f}\) streng monoton fällt. Dabei muss \(G_{f}\) im Koordinatenursprung die \(x\)-Achse unter einem Winkel von ca. 39° schneiden. bzw. die Steigung \(-\frac{\sf{4}}{\sf{5}}\) besitzen (siehe Teilaufgabe 1b).


