Ein Süßwarenunternehmen stellt verschiedene Sorten Fruchtgummis her.
Luisa nimmt an einer Betriebsbesichtigung des Unternehmens teil. Zu Beginn der Führung bekommt sie ein Tütchen mit zehn Gummibärchen, von denen fünf weiß. zwei rot und drei grün sind. Luisa öffnet das Tütchen und nimmt, ohne hinzusehen, drei Gummibärchen heraus. Berechnen Sie die Wahrscheinlichkeit dafür, dass die drei Gummibärchen die gleiche Farbe haben.
(3 BE)
Lösung zu Teilaufgabe 1

5 weiße, 2 rote und 3 grüne Gummibärchen
Die drei dem Tütchen entnommenen Gummibärchen können entweder alle weiß oder alle grün sein, nicht aber rot, da davon nur zwei enthalten sind.
1. Möglichkeit: Formel aus der Merkhilfe verwenden
Da die drei Gummibärchen einmalig entnommen werden, kann die Formel aus der Merkhilfe für das Urnenmodell „Ziehen ohne Zurücklegen" verwendet werden.
Urnenmodell: „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge"
Werden aus einer Urne mit \(N\) Kugeln, von denen \(K\) Kugeln schwarz sind, \(n\) Kugeln mit einem Griff, d.h. ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
\[\begin{align*}&\quad \enspace P(\text{„Alle drei Gummibärchen haben die gleiche Farbe"}) \\[0.8em] &= \frac{\displaystyle \overbrace{\binom{5}{3}}^{\text{alle weiß}} \cdot \binom{5}{0}}{\displaystyle \binom{10}{3}} + \frac{\displaystyle \overbrace{\binom{\textcolor{#89ba17}{3}}{\textcolor{#89ba17}{3}}}^{\textcolor{#89ba17}{\text{alle grün}}} \cdot \binom{7}{0}}{\displaystyle\binom{10}{3}} \\[0.8em]&= \frac{1}{12} + \frac{1}{120} \\[0.8em] &= \frac{11}{120} \approx 0{,}092 = 9{,}2\,\%\end{align*}\]
2. Möglichkeit: Baumdiagramm, Pfadregeln
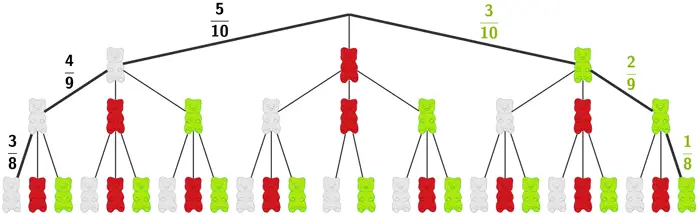
Es genügt die Betrachtung der beiden äußeren relevanten Pfade.
Drei weiße Gummibärchen (linker Pfad):
Aus einer Tüte mit 10 Gummibärchen, von denen 5 weiß sind, wird ein weißes Gummibärchen entnommen. Die Wahrscheinlichkeit dafür beträgt \(\frac{5}{10}\). Es verbleiben 9 Gummibärchen, von denen 4 weiß sind. Die Wahrscheinlichkeit dafür, ein zweites weißes Gummibärchen zu entnehmen, beträgt dann \(\frac{4}{9}\). Es verbleiben 8 Gummibärchen, von denen 3 weiß sind. Die Wahrscheinlichkeit dafür, ein drittes weißes Gummibärchen zu entnehmen, beträgt schließlich \(\frac{3}{8}\).
Die Beschreibung gilt analog für die drei grünen Gummibärchen (rechter Pfad).
Mithilfe der Pfadregeln ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}&\quad \;\,P(\text{„Die drei Gummibärchen haben die gleiche Farbe"}) \\[0.8em] &= \underbrace{\underbrace{\frac{5}{10} \cdot \frac{4}{9} \cdot \frac{3}{8}}_{\text{1 Pfadregel}} + \underbrace{\textcolor{#89ba17}{\frac{3}{10}} \cdot \textcolor{#89ba17}{\frac{2}{9}} \cdot \textcolor{#89ba17}{\frac{1}{8}}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em] &= \frac{1}{12} + \frac{1}{120} \\[0.8em] &= \frac{11}{120} \approx 0{,}092 = 9{,}2\,\%\end{align*}\]
Bildnachweis (Montage): Amberrose Nelson auf Pixabay


