Gegeben ist die in \(\mathbb R^{+}\) definierte Funktion \(h \colon x \mapsto 3x \cdot (-1 + \ln x)\).
Abbildung 1 zeigt den Graphen \(G_{h}\) von \(h\) im Bereich \(0{,}75 \leq x \leq 4\).
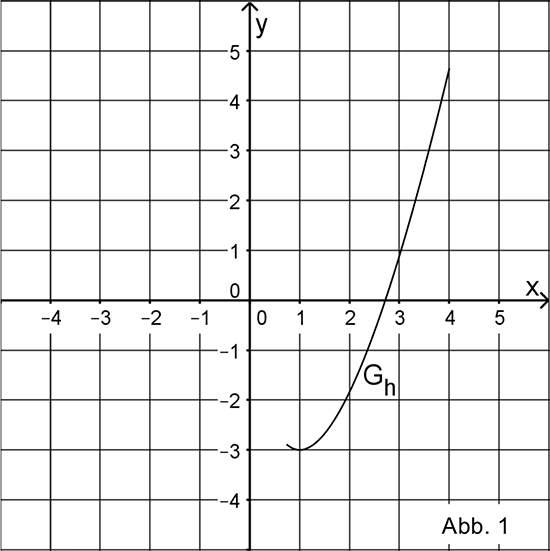
Bestimmen Sie die Gleichung der Tangente an \(G_{h}\) im Punkt \((e|0)\) und berechnen Sie die Größe des Winkels, unter dem diese Tangente die \(x\)-Achse schneidet.
(zur Kontrolle: \(h'(x) = 3 \cdot \ln x\))
(4 BE)
Lösung zu Teilaufgabe 1a
Gleichung einer Tangente an den Graphen einer Funktion, Steigungswinkel einer Geraden
\[h(x) = 3x \cdot (-1 + \ln{x}); \; D_{h} = \mathbb R^{+}\]
Gleichung der Tangente an \(G_{h}\) im Punkt \((e|0)\)
Der Ansatz für die Gleichung der Tangente \(T\) an den Graphen der Funktion \(h\) im Punkt \((e|0)\) kann mithilfe der allgemeinen Geradengleichung oder mit der Tangentengleichung erfolgen.
1. Lösungsansatz: Allgemeine Geradengleichung
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[T \colon y = m_{T} \cdot x + t\]
Die erste Ableitung \(h'\) an der Stelle \(x = e\) beschreibt die Steigung \(m_{T}\) der Tangente \(T\) an den Graphen der Funktion \(h\) im Punkt \((e|0)\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = h'(e)\]
Erste Ableitung \(h'\) bilden:
Die erste Ableitung \(h'\) lässt sich mithilfe der Produktregel, der Ableitung einer Potenzfunktion, der Ableitung der Natürlichen Logarithmusfunktion sowie der Summenregel formulieren.
\[h(x) = 3x \cdot (-1 + \ln{x})\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Ableitung der natürlichen Logarithmusfunktion:
\[f(x) = \ln x \quad (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
Summenregel
\[f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\]
(vgl. Merkhilfe)
\[\begin{align*} h'(x) &= 3 \cdot (-1 + \ln{x}) + 3x \cdot \left( 0 + \frac{1}{x} \right) \\[0.8em] &= -3 + 3\ln{x} + 3 \\[0.8em] &= 3\ln{x} \end{align*}\]
Tangentensteigung \(m_{T}\) berechnen:
\[\begin{align*} m_{T} &= h'(e) \\[0.8em] &= 3 \cdot \ln{e} & &| \; \ln{e} = 1; \; \text{allg.:}\; \log_{a}{a} = 1 \\[0.8em] &= 3 \cdot 1 \\[0.8em] &= 3 \end{align*}\]
Damit ergibt sich die Gleichung der Tangente \(T\) zu:
\[T \colon y = 3x + t\]
\(y\)-Achsenabschnitt \(t\) der Tangente \(T\) berechnen:
Die Tangente \(T\) berührt den Graphen der Funktion \(h\) im Punkt \((e|0) \in T\). Setz man die Koordinaten des Punktes \((e|0)\) in die Gleichung der Tangente \(T\) ein, lässt sich damit der \(y\)-Achsenabschnitt \(t\) berechnen.
\[\begin{align*} (e|0) \in T \colon 0 &= 3 \cdot e + t \\[0.8em] 0 &= 3e + t & &| - 3e \\[0.8em] -3e &= t \end{align*}\]
Gleichung der Tangente \(T\) angeben:
\[T \colon y = 3x - 3e\]
2. Lösungsansatz: Tangentengleichung
Mit dem Berührpunkt \((e|0)\) und \(h'(e) = 3\) (vgl. 1. Lösungsansatz) ergibt sich:
Gleichung einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\;(x_0|f(x_0)) \):
\[y = f'(x_{0}) \cdot (x - x_{0}) + f(x_{0})\]
\[\begin{align*} T \colon y &= h'(e) \cdot (x - e) + h(e) \\[0.8em] &= 3 \cdot (x - e) + 0 \\[0.8em] &= 3x - 3e \end{align*}\]
Größe des Winkels, unter dem die Tangente die \(x\)-Achse schneidet
Die Steigung der Tangente \(T\) ist mit \(m_{T} = 3\) positiv. In diesem Fall stimmt der Steigungswinkel \(\alpha\) der Tangente \(T\) mit der Größe des Winkels überein, unter dem die Tangente die \(x\)-Achse schneidet.
Für den Steigungswinkel \(\alpha\) einer Geraden gilt:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\tan{\alpha} = m\]
Dann gilt für den Steigungswinkel \(\alpha\) der Tangente \(T\):
\[\tan{\alpha} = m_{T}\]
Steigungswinkel \(\alpha\) der Tangente \(T\) berechnen:
\[T \colon y = 3x - 3e\]
\[\begin{align*}\tan{\alpha} &= m_{T} \\[0.8em] &= 3 & &| \; \text{TR:} \; \tan^{-1}(3) \\[2.4em] \alpha &\approx 71{,}57^{\circ}\end{align*}\]
Die Tangente \(T\) schneidet die \(x\)-Achse unter einem Winkel von ca. 71,57°.
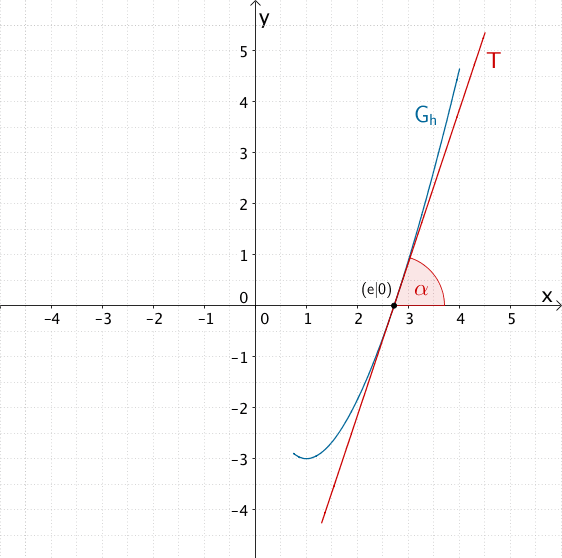
Tangente \(T\) an den Graphen \(G_{h}\) der Funktion \(h \colon x \mapsto 3x \cdot (-1 + \ln{x})\) im Punkt \((e|0)\); Winkel \(\alpha\), unter dem die Tangente \(T\) die \(x\)-Achse schneidet


