Um Geld für die Ausstattung des Spielbereichs in der Kinderstation des Krankenhauses einzunehmen, wird ein Gewinnspiel angeboten. Nachdem der Spieler zwei Euro bezahlt hat, werden aus einem Behälter, in dem sich drei rote, drei grüne und drei blaue Kugeln befinden, drei Kugeln ohne Zurücklegen zufällig entnommen. Haben die drei entnommenen Kugeln die gleiche Farbe, so gewinnt der Spieler und bekommt einen bestimmten Geldbetrag ausgezahlt; ansonsten verliert er und erhält keine Auszahlung. Anschließend werden die gezogenen Kugeln in den Behälter zurückgelegt.
Zeigen Sie, dass bei einem Spiel die Wahrscheinlichkeit für einen Gewinn \(\frac{1}{28}\) beträgt.
(2 BE)
Lösung zu Teilaufgabe 3a
Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge
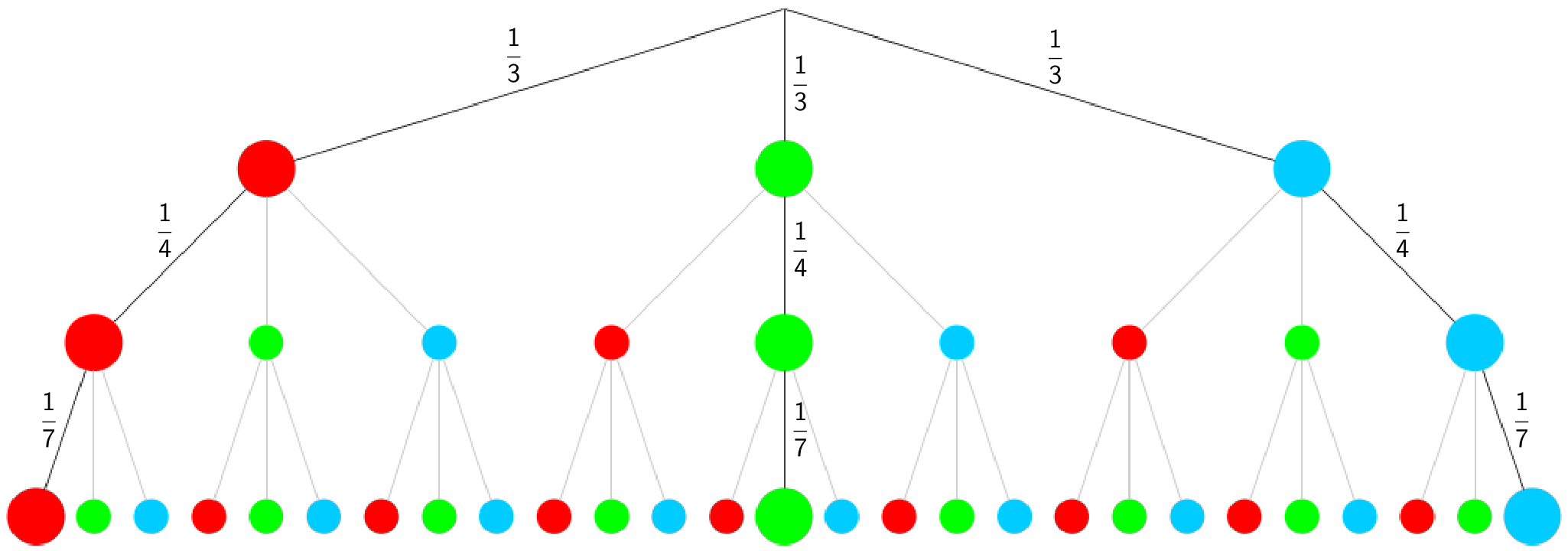
1. Lösugsansatz: Baumdiagramm (3-stufiges Zufallsexperiment)
Betrachtet werden die Ereignisse Rot, Grün und Blau.
Ziehen von drei Kugeln gleicher Farbe:
Beim ersten Ziehen ohne Zurücklegen beträgt die Wahrscheinlichkeit, eine Kugel der drei möglichen Farben Rot, Grün oder Blau zu ziehen \(\displaystyle \frac{3}{9} = \frac{1}{3}\).
Es verbleiben acht Kugeln, davon zwei Kugeln gleicher Farbe wie die Farbe der bereits gezogene Kugel.
Beim zweiten Ziehen ohne Zurücklegen beträgt die Wahrscheinlcihkeit, eine Kugel gleicher Farbe zu ziehen somit \(\displaystyle \frac{2}{8} = \frac{1}{4}\).
Es verbleiben noch sieben Kugeln, davon eine Kugel gleicher Farbe wie die Farbe der bereits gezogenen beiden Kugeln.
Beim dritten Ziehen beträgt die Wahrscheinlichkeit, eine weitere Kugel gleicher Farbe zu ziehen somit \(\displaystyle \frac{1}{7}\).
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Anwenden der 1. Pfadregel:
\[P(\text{Drei Kugeln gleicher Farbe}) = \frac{1}{3} \cdot \frac{1}{4} \cdot \frac{1}{7} = \frac{1}{84}\]
Es gibt drei Möglichkeiten drei Kugeln gleicher Farbe zu ziehen.
\[P(\text{Gewinn}) = 3 \cdot P(\text{Drei Kugeln gleicher Farbe}) = 3 \cdot \frac{1}{84} = \frac{1}{28} \]
2. Lösungsansatz: Ziehen mit einem Griff (1-stufiges Zufallsexperiment)
Da die Reihenfolge der gezogennen Kugeln keine Rolle spielt, macht es keinen Unterschied, ob diese nacheinander einzeln ohne Zurücklegen oder alle drei zusammen mit einem Griff gezogen werden. Betrachtet man die Kugeln einer Farbe als Treffer, so erhält man bei dem Spiel einen Gewinn, wenn mit einem Griff entweder drei rote, drei grüne oder drei blaue Kugeln gezogen werden.
Urnenmodell: „Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge"
Werden aus einer Urne mit \(N\) Kugeln, von denen \(K\) Kugeln schwarz sind, \(n\) Kugeln mit einem Griff, d.h. ohne Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gilt für die Wahrscheinlichkeit, genau \(k\) schwarze Kugeln zu ziehen:
\[P(\text{„genau}\,k\,\text{schwarze Kugeln"}) = \frac{\displaystyle \binom{K}{k} \cdot \binom{N - K}{n - k}}{\displaystyle \binom{N}{n}}\]
\[P(\text{Drei Kugeln gleicher Farbe}) = \frac{\displaystyle \binom{3}{3} \cdot \binom{6}{0}}{\displaystyle \binom{9}{3}} = \frac{1}{84}\]
Es gibt drei Möglichkeiten drei Kugeln gleicher Farbe zu ziehen.
\[P(\text{Gewinn}) = 3 \cdot P(\text{Drei Kugeln gleicher Farbe}) = 3 \cdot \frac{1}{84} = \frac{1}{28} \]
3. Lösungsansatz: Laplace-Wahrscheinlickeit
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
Anzahl der möglichen Ergebnisse:
Beim ersten Ziehen ohne Zurücklegen können neun von neun vorhandenen Kugeln gezogen werden. Beim zweiten Ziehen ohne Zurücklegen können acht von acht verbleibenden Kugeln gezogen werden. Beim dritten Ziehen können sieben von sieben verbleibenden Kugeln gezogen werden.
\[\text{Anzahl der möglichen Ergebnisse} = 9 \cdot 8 \cdot 7\]
Anzahl der günstigen Ergebnisse:
Ein günstiges Ergebnis im Sinne eines Gewinns sind drei Kugeln gleicher Farbe.
Beim ersten Ziehen ohne Zurücklegen gibt es neun Möglichkeiten, einen Kugel zu ziehen. Beim zweiten Ziehen ohne Zurücklegen gibt es zwei Möglichkeiten, eine Kugel gleicher Farbe zu ziehen. Beim dritten Ziehen gibt es eine Möglichkeit, eine Kugel gleicher Farbe zu ziehen.
\[\text{Anzahl der günstigen Ergebnisse} = 9 \cdot 2 \cdot 1\]
\[P(\text{Gewinn}) = \frac{\text{Anzahl der günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}} = \frac{9 \cdot 2 \cdot 1}{9 \cdot 8 \cdot 7} = \frac{1}{28}\]