Bestimmen Sie die Größe des Winkels, den \(L\) mit der \(x_1x_2\)-Ebene einschließt.
(3 BE)
Lösung zu Teilaufgabe b
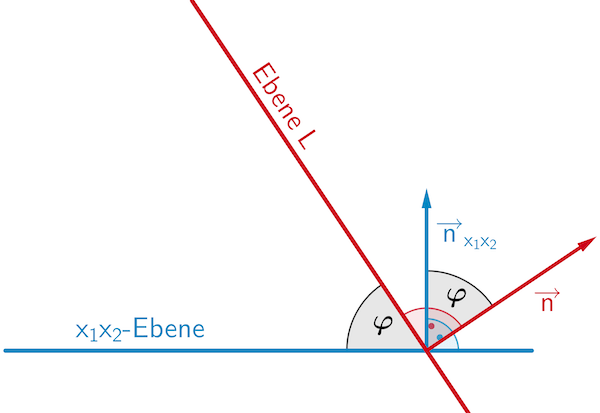
Der Winkel, den die Ebene \(\textcolor{#cc071e}{L}\) mit der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene einschließt (Schnittwinkel), ist gleich dem Winkel zwischen den Normalenvektoren der Ebenen (Skizze schematisch, nicht verlangt).
\(\textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}}\) ist ein Normalenvektor der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene.
\(\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix}}\) ist ein Normalenvektor der Ebene \(\textcolor{#cc071e}{L}\) (vgl. Teilaufgabe a).
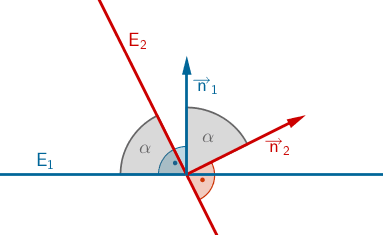
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
\[\begin{align*} \cos{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{n}} \circ \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{n}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert} = \frac{\left| \textcolor{#cc071e}{\begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix}} \circ \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right|}{\left| \textcolor{#cc071e}{\begin{pmatrix} 2 \\ 4 \\ 3 \end{pmatrix}} \right| \cdot \left| \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right|} \\[0.8em] &= \frac{\vert \textcolor{#cc071e}{2} \cdot \textcolor{#0087c1}{0} + \textcolor{#cc071e}{4} \cdot \textcolor{#0087c1}{0} + \textcolor{#cc071e}{3} \cdot \textcolor{#0087c1}{1} \vert}{\sqrt{\textcolor{#cc071e}{2}^2 + \textcolor{#cc071e}{4}^2 + \textcolor{#cc071e}{3}^2} \cdot \sqrt{\textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{1}^2}} \\[0.8em] &= \frac{3}{\sqrt{29}} &&| \; \text{TR:}\; \cos^{-1}(\dots) \\[2.4em] \varphi &= \cos^{-1}\left( \frac{3}{\sqrt{29}} \right) \approx 56{,}15^{\circ}\end{align*}\]
Die Größe \(\varphi\) des Winkels, den \(L\) mit der \(x_1x_2\)-Ebene einschließt, beträgt etwa 56°.


