Die beiden Baumdiagramme gehören zum selben Zufallsexperiment mit den Ereignissen \(A\) und \(B\).
Berechnen Sie die Wahrscheinlichkeit \(P(B)\) und ergänzen Sie anschließend an allen Ästen des rechten Baumdiagramms die zugehörigen Wahrscheinlichkeiten.
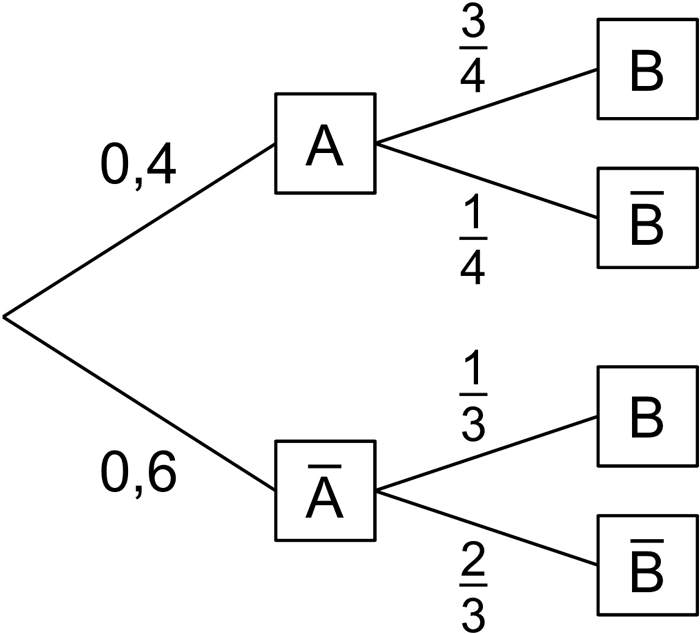
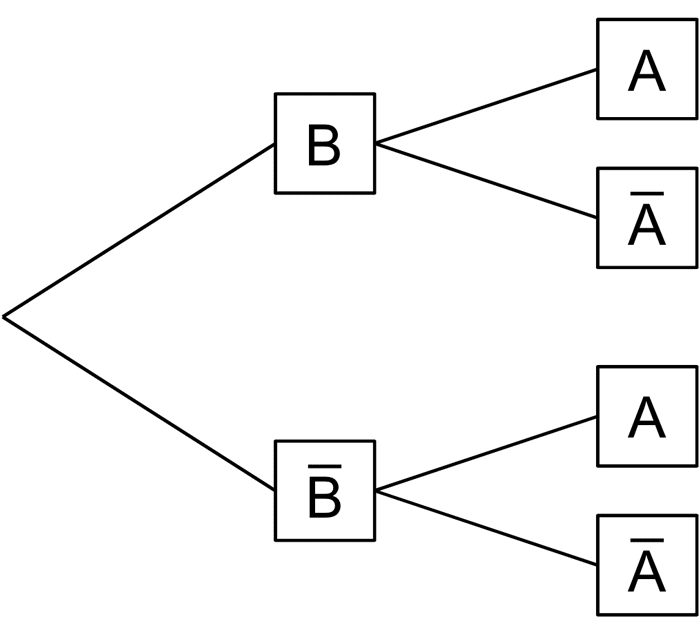
(Teilergebnis: \(P(B) = 0{,}5\))
(5 BE)
Lösung zu Teilaufgabe 1
Anmerkung: Wegen der besseren Lesbarkeit, werden die beiden Baumdiagramme in der Ansicht mit mobilen Endgeräten ggf. untereinander angezeigt. Das gemäß Angabe rechte Baumdiagramm erscheint dann unterhalb des linken Baumdiagramms.
Baumdiagramm und Pfadregeln, Bedingte Wahrscheinlichkeit
Berechnung der Wahrscheinlichkeit \(P(B)\)

Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Die Wahrscheinlichkeit \(P(B)\) für das Eintreten des Ereignisses \(B\) lässt sich mithilfe der 1. und der 2. Pfadregel berechnen.
\[\begin{align*} P(B) &= P(A \cap B) + P((\overline{A} \cap B)) \\[0.8em] &= \underbrace{\underbrace{0{,}4 \cdot \frac{3}{4}}_{\large \text{1. Pfadregel}} + \underbrace{0{,}6 \cdot \frac{1}{3}}_{\large \text{1. Pfadregel}}}_{\large \text{2. Pfadregel}} \\[0.8em] &= \frac{4}{10} \cdot \frac{3}{4} + \frac{6}{10} \cdot \frac{1}{3} \\[0.8em] &= \frac{3}{10} + \frac{2}{10} \\[0.8em] &= \frac{5}{10} \\[0.8em] &= 0{,}5 \end{align*}\]
Wahrscheinlichkeiten des rechten Baumdiagramms


Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
Das linke Baumdiagramm erlaubt mithilfe der 1. Pfadregel die Berechnung aller Wahrscheinlichkeiten der Schnittmengen \(A \cap B\), \(A \cap \overline{B}\), \(\overline{A} \cap B\) und \(\overline{A} \cap \overline{B}\). Diese lassen sich auf das rechte Baumdiagramm übertragen. Zusammen mit der bereits bekannten Wahrscheinlichkeit \(P(B)\) können damit die bedingten Wahrscheinlichkeiten \(P_{B}(A)\), \(P_{B}(\overline{A})\), \(P_{\overline{B}}(A)\) und \(P_{\overline{B}}(\overline{A})\) berechnet werden.
\[P(A \cap B) = 0{,}4 \cdot \frac{3}{4} = 0{,}3 = P(B \cap A)\]
\[P(A \cap \overline{B}) = 0{,}4 \cdot \frac{1}{4} = 0{,}1 = P(\overline{B} \cap A) \]
\[P(\overline{A} \cap B) = 0{,}6 \cdot \frac{1}{3} = 0{,}2 = P(B \cap \overline{A})\]
\[P(\overline{A} \cap \overline{B}) = 0{,}6 \cdot \frac{2}{3} = 0{,}4 = P(\overline{B} \cap \overline{A})\]
\[P(B) = 0{,}5 \quad \Longrightarrow \quad P(\overline{B}) = 0{,}5\]
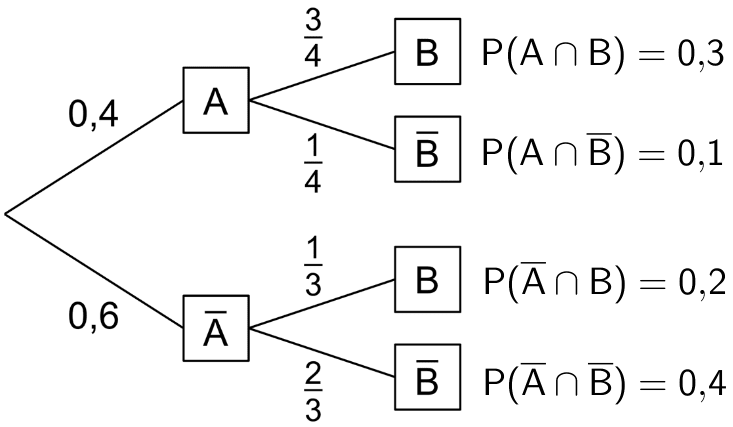
Linkes Baumdiagramm mit den Eintragungen der Wahrscheinlichkeiten der Schnittmengen an den Enden der Pfade.
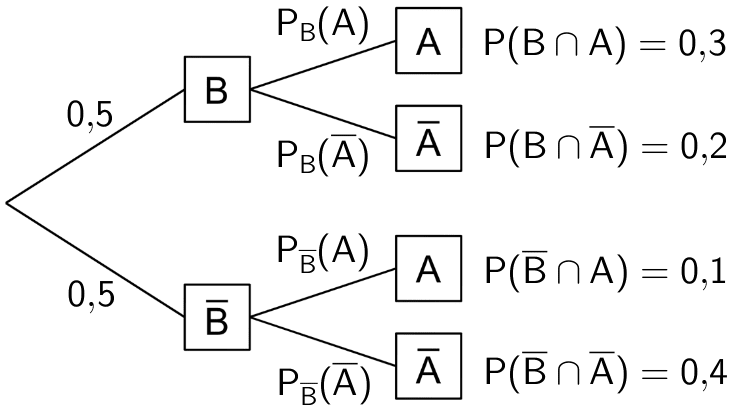
Rechtes Baumdiagramm mit den Eintragungen der Wahrscheinlichkeiten der Schnittmengen an den Enden der Pfade sowie der Benennung der bedingten Wahrscheinlichkeiten an den Pfaden der zweiten Stufe des Zufallsexperiments.
Bedingte Wahrscheinlichkeiten \(P_{B}(A)\), \(P_{B}(\overline{A})\), \(P_{\overline{B}}(A)\) und \(P_{\overline{B}}(\overline{A})\) berechnen:
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_{B}(A) = \frac{P(B \cap A)}{P(B)} = \frac{0{,}3}{0{,}5} = 0{,}6\]
Knotenregel anwenden:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P_{B}(\overline{A}) = 1 - P_{B}(A) = 1 - 0{,}6 = 0{,}4\]
\[P_{\overline{B}}(A) = \frac{P(\overline{B} \cap A)}{P(\overline{B})} = \frac{0{,}1}{0{,}5} = 0{,}2\]
Knotenregel anwenden:
\[P_{\overline{B}}(\overline{A}) = 1 - P_{\overline{B}}(A) = 1 - 0{,}2 = 0{,}8\]
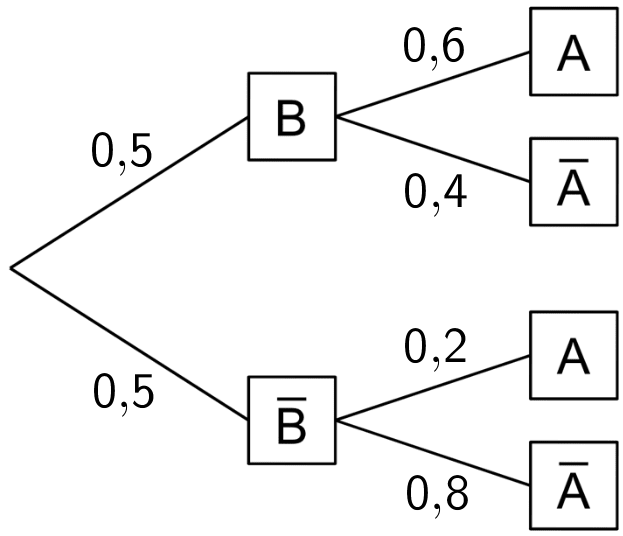
Rechtes Baumdiagramm mit den Eintragungen der Wahrscheinlichkeiten an allen Ästen des Baumdiagramms

