Der Tourismusverband vermutet, dass sich der bisherige Anteil der Radausflügler unter den Touristen von 15 % durch den Einsatz der Shuttlebusse erhöht hat. Die Verantwortlichen planen die Durchführung eines Signifikanztests mit einem Signifikanzniveau von 8 % und der Nullhypothese „Der Anteil der Radausflügler unter allen Touristen liegt bei höchstens 15 %." Vor der Durchführung des Tests wird festgelegt, die Shuttlebusses nur dann weiterzubetreiben, wenn die Nullhypothese aufgrund des Testergebnisses abgelehnt wird.
Es ist geplant, den Test auf der Grundlage einer Stichprobe von 200 Touristen durchzuführen. Bestimmen Sie die zugehörige Entscheidungsregel.
(5 BE)
Lösung zu Teilaufgabe 2c
\(Y\): Anzahl der Radausflügler unter einer Stichprobe von 200 Touristen
Signifikanzniveau: \(\textcolor{#0087c1}{8\,\%}\)
„... Nullhypothese „Der Anteil der Radausflügler unter allen Touristen liegt bei höchstens 15 %."
\[H_0\colon p \textcolor{#e9b509}{\leq 0{,}15}\]
Die Nullhypothese wird abgelehnt, wenn viele der 200 Touristen Radausflügler sind.
Annahmebereich \(A = \{0; 1; 2; \dots; g - 1\}\)
Ablehnungsbereich \(\textcolor{#cc071e}{\overline{A} = \{g; g + 1; \dots; 200\}}\)

Ein Signifikanztest gibt der Wahrscheinlichkeit für den Fehler 1. Art \(\alpha'\) eine Obergrenze vor, das sog. Signivikanzniveau \(\alpha\). Die Bedingung \(\alpha' \leq \alpha\) liefert eine Entscheidungsregel dafür, wie ein Stichprobenergebnis hinsichtlich einer zu testenden Vermutung zu bewerten ist.
\[\begin{align*}\alpha' &\leq \alpha \\[0.8em] P(\text{Fehler 1. Art}) &\leq \alpha \end{align*}\]
Welchen Fehler im Sachzusammenhang der Fehler 1. Art vertritt, hängt von der Wahl der Nullhypothese ab.
Die Nullhypothese wird bei einem Signifikanztest in der Regel so gewählt, dass der Fehler 1. Art einen im Sachzusammenhang als schwerwiegend erachteten Fehler beschreibt, der kontrolliert werden soll.
Fehler 1. Art: Die Nullhypothese wird irrtümlich abgelehnt.
Nennt die Aufgabenstellung zum Thema Signifikanztest
- einen Fehler, der begrenzt werden soll, lässt sich daraus auf die Nullhypothese schließen. Hierfür wird die Frage beantwortet: Wie muss die Nullhypothese lauten, damit deren irrtümliche Ablehnung zum genannten Fehler führt.
- eine Nullhypothese, lässt sich daraus auf den zu vermeidenden Fehler schließen (Grund für die Wahl der Nullhypothese). Hierfür wird die Frage beantwortet: Welcher Fehler tritt ein, wenn die Nullhypothese irrtümlich abgelehnt wird?
Vorgehensweise - Einseitiger Signifikanztest
- Testgröße \(X\) (binomialverteilte Zufallsgröße) und Stichprobenumfang \(n\) sowie Nullhypothese \(H_0\) und Gegenhypothese \(H_1\) erkennen und notieren.
- Kritischen Bereich \(\textcolor{#cc071e}{K}\) (Ablehnungsbereich) der Nullhypothese mit unbekannter Grenze \(g\) vorformulieren.
- Signifikanztest durchführen und Entscheidungsregel formulieren.
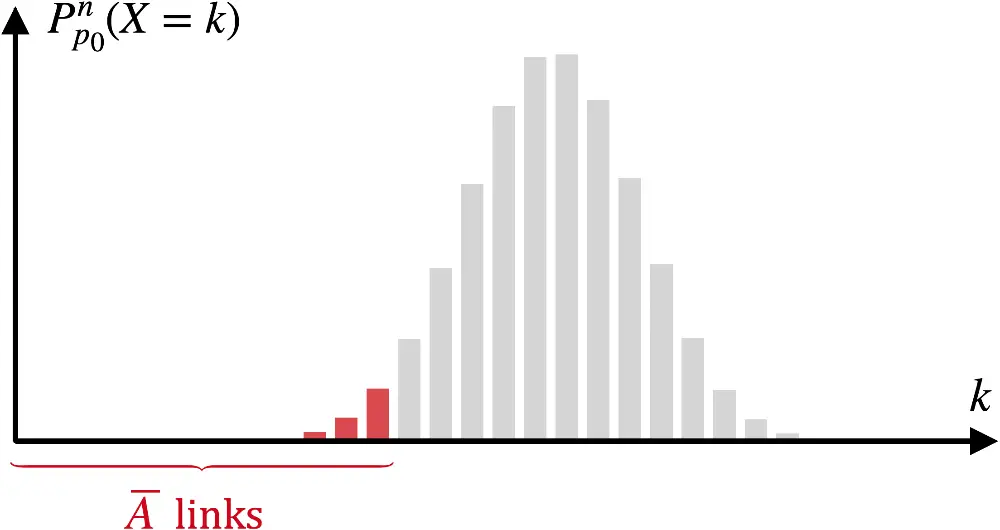
Linksseitiger Signifikanztest
\(H_0\colon p = p_0\) oder \(H_0\colon p \geq p_0\)
\(H_1\colon p < p_0\)
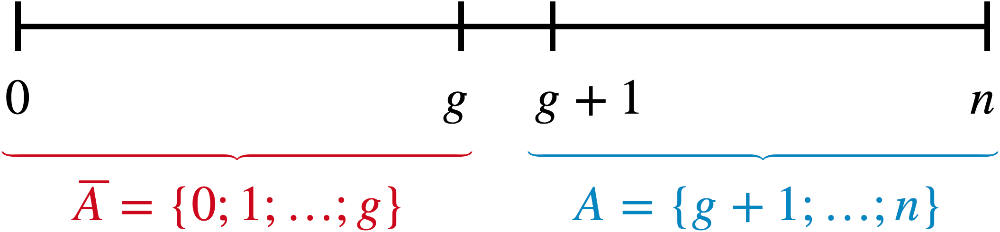
\[\begin{align*} \alpha' &\leq \alpha \\[0.8em] P(\text{Fehler 1. Art}) &\leq \alpha \\[0.8em] P_{p_0}^n(X \in \textcolor{#cc071e}{K}) &\leq \alpha \\[0.8em] P_{p_0}^n(X \textcolor{#cc071e}{\leq g}) &\leq \alpha \\[0.8em] \sum \limits_{i\,=\,\textcolor{#cc071e}{0}}^{\textcolor{#cc071e}{g}}B(n;p_0;i)&\leq \alpha && \overset{\text{WTR/TW}}{\Longrightarrow} \; \textcolor{#cc071e}{g} \end{align*}\]
Rechtsseitiger Signifikanztest
\(H_0\colon p = p_0\) oder \(H_0\colon p \leq p_0\)
\(H_1\colon p > p_0\)
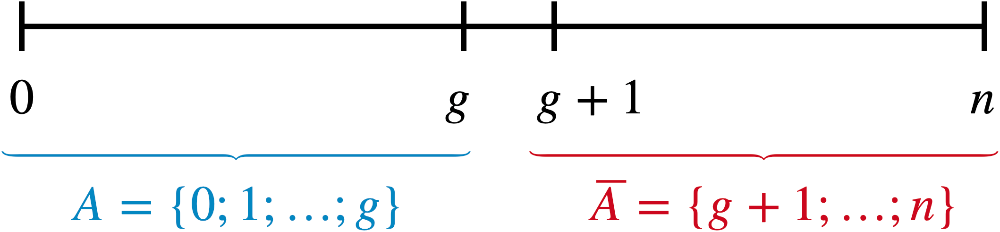
\[\begin{align*} \alpha' &\leq \alpha \\[0.8em] P(\text{Fehler 1. Art}) &\leq \alpha \\[0.8em] P_{p_0}^n(X \in \textcolor{#cc071e}{K}) &\leq \alpha \\[0.8em] P_{p_0}^n(X \textcolor{#cc071e}{\geq g}) &\leq \alpha \\[0.8em] 1 - P_{p_0}^n(X \textcolor{#0087c1}{\leq g-1}) &\leq \alpha &&| - 1 \\[0.8em] - P_{p_0}^n(X \textcolor{#0087c1}{\leq g-1}) &\leq \alpha -1 &&| \cdot (-1) \\[0.8em] P_{p_0}^n(X \textcolor{#0087c1}{\leq g-1}) &\geq 1 -\alpha \\[0.8em] \sum \limits_{i\,=\,\textcolor{#0087c1}{0}}^{\color{#0087c1}g\,-\,1}B(n;p_0;i) &\geq 1- \alpha &&\overset{\text{WTR/TW}}{\Longrightarrow}\; \textcolor{#0087c1}{g-1}\end{align*}\]
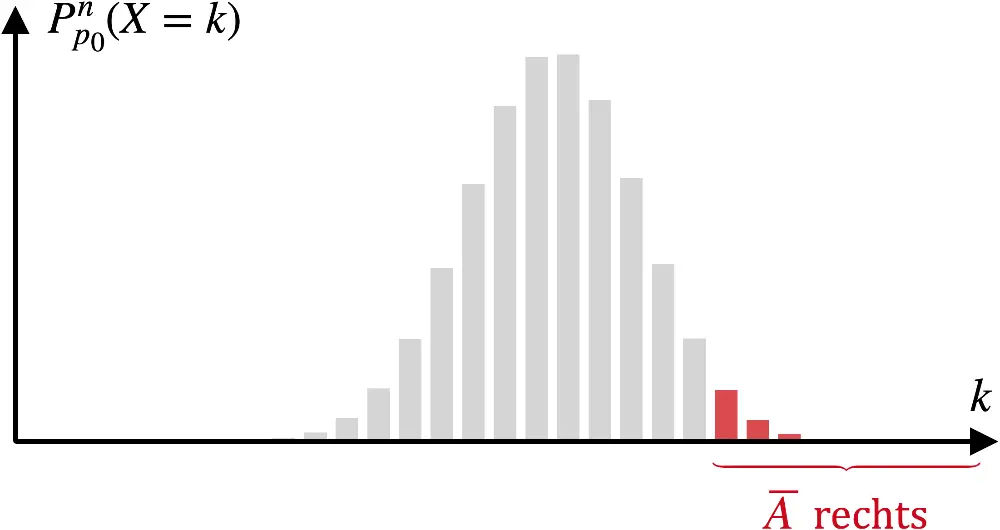
Rechtsseitiger Signifikanztest (Ablehnungsbereich liegt „rechts"):
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich nicht abgelehnt.
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | richtige Entscheidung |
| \(H_{0}\) wird nicht abgelehnt | richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P(\text{Fehler 1. Art}) = P^{n}_{p_0} (X \in K)\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P(\text{Fehler 2. Art}) = P^n_{p_{1}} (X \in \overline{K})\]
Um die Wahrscheinlichkeit für den Fehler 2. Art berechnen zu können, muss eine Annahme für die Wahrscheinlichkeit \(p_1\) der Gegenhypothese \(H_1\) getroffen werden.
Die Wahrscheinlichkeit für den Fehler 2. Art kann weit über 50 % betragen. Deshalb lässt sich nicht folgern, dass die Nullhypothese tatsächlich gilt, nur weil sie nicht abgelehnt wird.
\(K\): kritischer Bereich (Ablehnungsbereich) der Nullhypothese
\(\overline{K}\): nichtkritischer Bereich der Nullhypothese
\[\begin{align*} P(\text{Fehler 1. Art}) &\textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}08} &&| \;H_0\;\textcolor{#cc071e}{\text{wird abgelehnt}}\text{,}\;\textcolor{#e9b509}{\text{obwohl sie zutrifft}} \\[0.8em] P_{\textcolor{#e9b509}{0{,}15}}^{200}(Y \in \textcolor{#cc071e}{\overline{A}}) &\textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}08} &&|\; \textcolor{#cc071e}{\overline{A} = \{g;g+1; \dots ; 200\}} \\[0.8em] P_{\textcolor{#e9b509}{0{,}15}}^{200}(Y \textcolor{#cc071e}{\geq g}) &\textcolor{#0087c1}{\leq} \textcolor{#0087c1}{0{,}08} &&|\; \text{Gegenereignis betrachten} \\[0.8em] 1 - P_{0{,}15}^{200}(Y \leq g - 1) &\leq 0{,}08 &&| - 1 \\[0.8em] - P_{0{,}15}^{200}(Y \leq g - 1) &\leq -0{,}92 &&| \cdot (-1)\; \text{Relationszeichen dreht sich} \\[0.8em] P_{0{,}15}^{200}(Y \leq k - 1) &\geq 0{,}92 &&| \; \text{Tafelwerk (TW) verwenden} \end{align*}\]
\(\overset{\text{TW}}{\Rightarrow} g - 1 = 37 \Rightarrow \textcolor{#cc071e}{g = 38}\)
Mit \(P_{0{,}15}^{200}(Y \textcolor{#cc071e}{\geq 38}) = 1 - P_{0{,}15}^{200}(Y \leq 37) \approx 0{,}072 < \textcolor{#0087c1}{0{,}08}\)
und \(P_{0{,}15}^{200}(Y \geq 37) = 1 - P_{0{,}15}^{200}(Y \leq 36) \approx 0{,}101 > \textcolor{#0087c1}{0{,}08}\)
Damit ist \(\textcolor{#cc071e}{g = 38}\) die untere Grenze des Ablehnungsbereichs der Nullhypothese, also \(\textcolor{#cc071e}{\overline{A} = \{38; 39; \dots\; 200\}}\).
Die Nullhypothese wird abgelehnt, wenn unter der Stichprobe von 200 Touristen mindestens 38 Radausflügler sind.


