Beim Atmen ändert sich das Luftvolumen in der Lunge. Geben Sie auf der Grundlage des Modells einen Zeitpunkt an, zu dem das Luftvolumen in der Lunge der Testperson minimal ist, und machen Sie Ihre Antwort mithilfe von Abbildung 5 plausibel.
(2 BE)
Lösung zu Teilaufgabe 3b
Funktionsgraph im Sachzusammenhang interpretieren
\[g(t) = -\frac{\pi}{8} \sin \left( \frac{\pi}{2}t \right)\,; \enspace D = \mathbb R_{0}^{+}\]
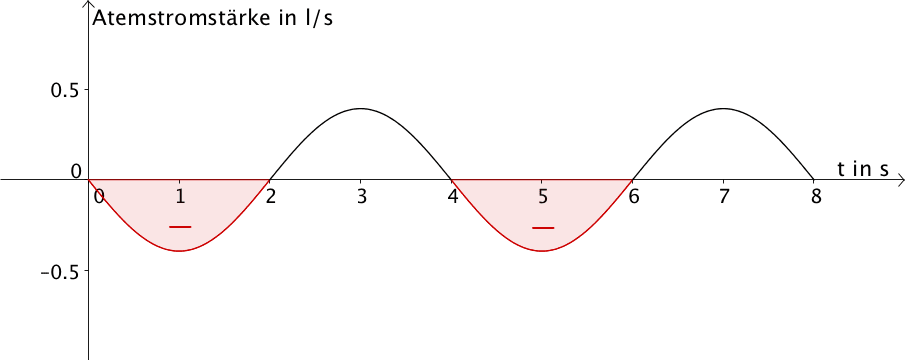
Für \(t \in \; ]0;2[\) und \(t \in \; ]4;6[\) verläuft der Graph der Funktion \(g\) unterhalb der \(t\)-Achse. Demnach atmet die Testperson während der ersten beiden Sekunden sowie in der Zeit zwischen der vierten und sechsten Sekunde seit Beobachtungsbeginn aus (siehe Teilaufgabe 3a). Das Integral \(\displaystyle \int_{0}^{2}g(t)\,dt\) bzw. \(\displaystyle \int_{4}^{6}g(t)\,dt\) errechnet jeweils das Luftvolumen, welches die Testperson während dieser jeweils zwei Sekunden ausatmet. Folglich ist das Luftvolumen in der Lunge der Testperson im Betrachteten Zeitraum \(t \in [0;8]\) zum Zeitpunkt \(t = 2\) Sekunden und \(t = 6\) Sekunden jeweils minimal.


