Der Tunnel soll durch einen Berg führen. Im betrachteten Querschnitt wird das Profil des Berghangs über dem Tunnel durch eine Gerade \(g\) mit der Gleichung \(y = -\frac{4}{3}x + 12\) modelliert.
Zeigen Sie, dass die Tangente \(t\) an den Graphen von \(f\) im Punkt \(R(4|f(4))\) parallel zu \(g\) verläuft. Zeichnen Sie \(g\) und \(t\) in das Koordinatensystem aus Aufgabe 3a ein.
(4 BE)
Lösung zu Teilaufgabe 3d
Tangentensteigung, Parallelität zweier Geraden
\[g \colon y = -\frac{4}{3}x + 12\]
\[f(x) = \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\]
\[R(4|f(4))\]
Nachweis, dass die Tangente \(t\) parallel zu \(g\) verläuft
Die Tangente \(t\) an den Graphen der Funktion \(f\) im Punkt \(R(4|f(4))\) verläuft parallel zur Geraden \(g\), wenn die Tangentensteigung \(m_{t}\) gleich der Steigung \(m_{g}\) der Geraden \(g\) ist.
Zueinander parallele / senkrechte (orthogonale) Geraden
\[g_1 \colon y = m_1\cdot x + t_1; \enspace g_2 \colon y = m_2\cdot x + t_2\]
parallele Geraden:
\[m_1 = m_2 \; \Leftrightarrow \; g_1 \parallel g_2\]
senkrechte (orthogonale) Geraden:
\[m_1 \cdot m_2 = -1 \; \Leftrightarrow \; g_1 \perp g_2\]
\[m_{t} = m_{g}\]
\[g \colon y = -\frac{4}{3}x + 12 \quad \Longrightarrow \quad m_{g} = -\frac{4}{3}\]
Steigung \(m_{t}\) der Tangente \(t\):
Die Ableitungsfunktion \(f'\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{t} = f'(4)\]
Erste Ableitung \(f'\) bilden:
Die erste Ableitung \(f'\) der Funktion \(f\) kann mithilfe der Ableitung einer Wurzelfunktion bzw. der Ableitung einer Potenzfunktion sowie unter Berücksichtigung der Ketten- und der Summenregel gebildet werden.
Als Alternative formuliert man den Wurzelterm in der Porenschreibweise und leitet anschließend mithilfe der Ableitung einer Potenzfunktion sowie unter Berücksichtigung der Ketten- und der Summenregel ab.
\[f(x) = \sqrt{25 - x^{2}}\]
Ableitung einer Wurzelfunktion
\[f(x) = \sqrt{g(x)} \quad \Longrightarrow \quad f'(x) = \frac{g'(x)}{2\sqrt{g(x)}} \quad (g(x) \geq 0)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= \frac{-\cancel{2} \cdot x}{\cancel{2} \sqrt{25 - x^{2}}} \\[0.8em] &= -\frac{x}{\sqrt{25 - x^{2}}} \end{align*}\]
oder
\[\begin{align*}f(x) &= \sqrt{25 - x^{2}} & &| \; \sqrt[n]{a} = a^{\frac{1}{n}} \\[0.8em] &= \left( 25 - x^{2} \right)^{\frac{1}{2}} \end{align*}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= \frac{1}{2} \cdot \left( 25 - x^{2} \right)^{-\frac{1}{2}} \cdot (-2x) & &| \; a^{\frac{1}{n}} = \sqrt[n]{a}; \enspace a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \frac{-\cancel{2} \cdot x}{\cancel{2} \sqrt{25 - x^{2}}} \\[0.8em] &= -\frac{x}{\sqrt{25 - x^{2}}} \end{align*}\]
Tangentensteigung \(m_{t}\) berechnen:
\[f'(x) = -\frac{x}{\sqrt{25 - x^{2}}}\]
\[\begin{align*} m_{t} &= f'(4) \\[0.8em] &= - \frac{4}{\sqrt{25 - 4^{2}}} \\[0.8em] &= -\frac{4}{\sqrt{9}} \\[0.8em] &= -\frac{4}{3} \end{align*}\]
Steigungen \(m_{t}\) der Tangente \(t\) und \(m_{g}\) der Geraden \(g\) vergleichen:
\[m_{t} = -\frac{4}{3}; \enspace m_{g} = -\frac{4}{3}\]
\[\Longrightarrow \quad m_{t} = m_{g} \quad \Longrightarrow \quad t \parallel g\]
Einzeichen von \(g\) und \(t\) in das Koordinatensystem aus Teilaufgabe 3a
\[g \colon y = -\frac{4}{3}x + 12\]
\[f(x) = \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\]
\[R(4|f(4))\]
\[R \in t, \; t \parallel g\]
\[f(4) = \sqrt{25 - 4^{2}} = \sqrt{9} = 3\]
\[\Longrightarrow \quad R(4|3)\]
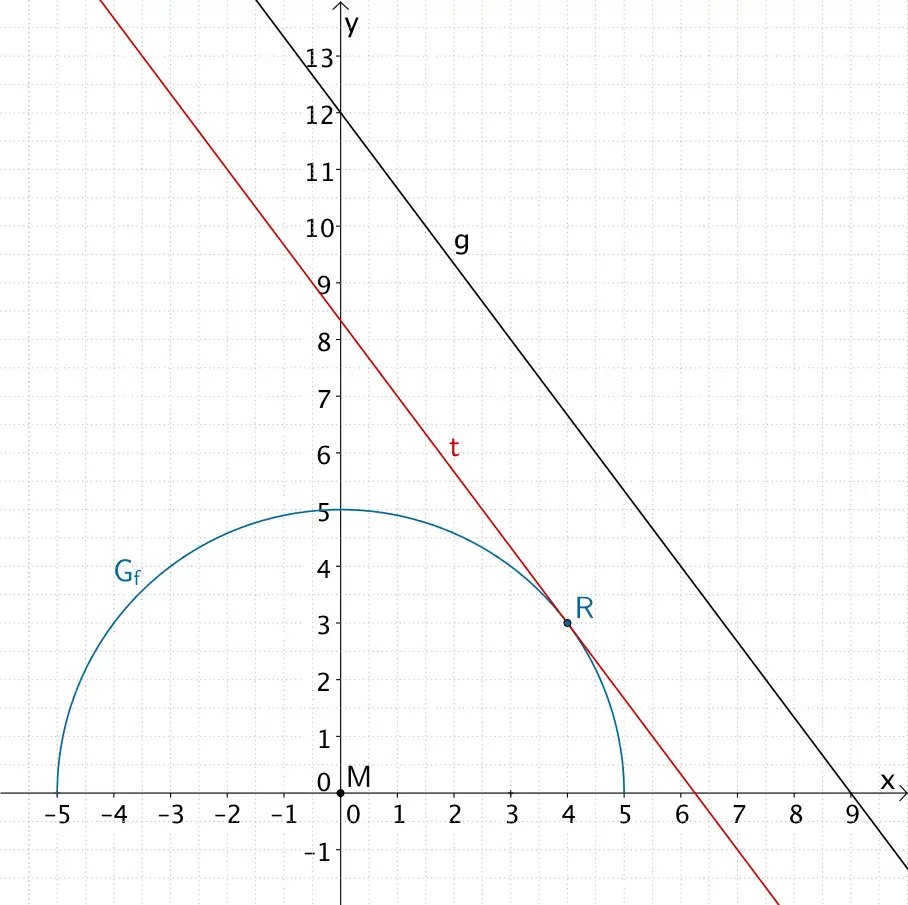
Graph der Funktion \(f \colon x \mapsto \sqrt{25 - x^{2}}; \; D_{f} = [-5;5]\), Gerade \(g \colon y = -\frac{4}{3}x + 12\) und Tangente \(t\) an \(G_{f}\) in \(R(4|3)\) mit \(t \parallel g\)


