Die Abbildung zeigt eine nach unten geöffnete Parabel, die zu einer Funktion \(f\) mit Definitionsbereich \(\mathbb R\) gehört. Der Scheitel der Parabel hat die \(x\)-Koordinate 3.
Betrachtet wird die in \(\mathbb R\) definierte Integralfunktion \(\displaystyle F \colon x \mapsto \int_{3}^{x}f(t) dt\).
Wie viele Nullstellen hat \(F\)?. Machen Sie Ihre Antwort ohne Rechnung plausibel.
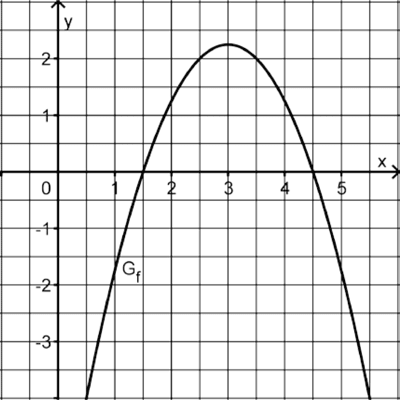
(4 BE)
Lösung zu Teilaufgabe 3
Die Integralfunktion \(\displaystyle F \colon x \mapsto \int_{3}^{x}f(t) dt\) hat genau drei Nullstellen.
Integralfunktion
Eine Funktion der Form \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\,dt\) mit einer festen unteren Integrationsgrenze \(a \in D_{f}\) und einer variablen oberen Integrationsgrenze heißt Integralfunktion von \(f\) zur unteren Grenze \(a\).
Erste Nullstelle von \(F\)
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Jede Integralfunktion hat an der unteren Integrationsgrenze eine Nullstelle. Die Intergarlfunktion \(\displaystyle F \colon x \mapsto \int_{3}^{x}f(t) dt\) besitzt also die Nullstelle \(x_{1} = 3\).
Zweite und dritte Nullstellen von \(F\)
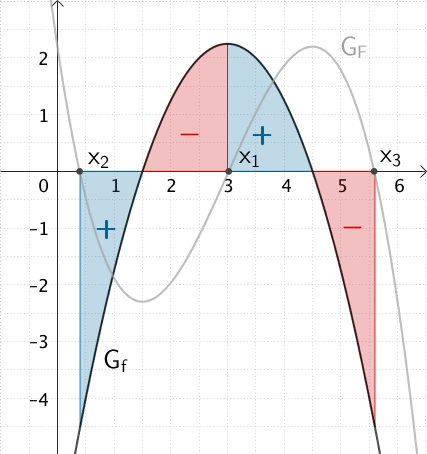
Für alle \(x \in \mathbb R\) lässt sich der Wert der Integralfunktion \(F\) als Flächenbilanz der Flächenstücke interpretieren, welche \(G_{f}\) mit der \(x\)-Achse einschließt.
Es gibt eine Stelle \(x_{2} < 1{,}5\), sodass \(G_{f}\) mit der \(x\)-Achse zwei flächeninhaltsgleiche Flächenstücke einschließt, von denen eines oberhalb und eines unterhalb der \(x\)-Achse liegt (unterschiedliche Vorzeichen). Somit ist die Flächenbilanz von \(F(x_{2})\) gleich Null. Das heißt, \(F\) hat an der Stelle \(x_{2}\) eine zweite Nullstelle \((x_{2} \approx 0{,}4)\).
Analog gilt: Es gibt eine Stelle \(x_{3} > 4{,}5\), sodass die Flächenbilanz von \(F(x_{3})\) gleich Null ist. Also ist \(x_{3}\) eine dritte Nullstelle von \(F\) \((x_{3} \approx 5{,}6)\).
Anmerkung:
Für \(x < 3\) ist die obere Integrationsgrenze der Integralfunktion \(\displaystyle F \colon x \mapsto \int_{3}^{x}f(t) dt\) kleiner als die feste untere Integrationsgrenze. Deshalb gehen Flächenstücke oberhalb der \(x\)-Achse negativ und Flächenstücke unterhalb der \(x\)-Achse positiv in die Flächenbilanz ein.
Während sich die erste Nullstelle mit \(x_{1} = 3\) exakt benennen lässt, müssen die zweite und dritte Nullstelle \(x_{2}\) und \(x_{3}\) nicht näherungsweise genannt werden. Es genügt zu begründen, weshalb \(F\) für \(x < 1{,}5\) und \(x > 4{,}5\) Nullstellen besitzt.
Begründung, weshalb es keine weiteren Nullstellen geben kann
Da \(G_{f}\) sowohl für \(x < 1{,}5\) als auch für \(x > 4{,}5\) stets unterhalb der \(x\)-Achse verläuft, kann es neben den genannten Nullstellen keine weitere Stelle \(x\) geben, an der die Flächenbilanz der Integralfunktion \(F\) gleich Null ist.
Alternative Begründung:
Die abgebildete Parabel ist der Graph einer ganzrationalen Funktion 2. Grades (quadratische Funktion). Jede zugehörige Integralfunktion ist eine ganzrationale Funktion 3. Grades, welche maximal drei Nullstellen haben kann.


