Geben Sie den Term einer gebrochen-rationalen Funktion \(f\) mit Definitionsmenge \(\mathbb R \backslash \{-1\}\) an, deren Graph die Gerade mit der Gleichung \(y = 2\) als Asymptote besitzt und in \(x = -1\) eine Polstelle ohne Vorzeichenwechsel hat.

(3 BE)

Lösung zu Teilaufgabe 4

Mögliche Funktionsterme sind z.B.:

\[f(x) = 2 + \frac{1}{(x + 1)^2}\]

oder

\[f(x) = 2 + \frac{x}{(x + 1)^2}\]

oder

\[f(x) = \frac{2x^2}{(x + 1)^2}\]

Vorgehensweise:

1. Bedingung:

\(D_f = \mathbb R \backslash \{-1\}\)

\(x = -1\) ist Polstelle ohne Vorzeichenwechsel

\(\Longrightarrow \quad\) Der Nenner von \(f\) hat für \(x = -1\) eine Nullstelle gerader Ordnung, die nicht gleichzeitig Nullstelle des Zählers ist.

\(\Longrightarrow \quad\) z.B. Nennerterm: \(h(x) = (x + 1)^2\)

2. Bedingung:

\(y = 2\) ist Asymptote

\(\Longrightarrow \quad\) Ansatz: \(f(x) = 2 \pm g(x) \,\), wobei gilt: \(\lim \limits_{x \, \to \, \pm \infty} g(x) = 0\)

\(\Longrightarrow \quad\) z.B. \(\displaystyle f(x) = 2 + \frac{1}{(x + 1)^2}\)

Alternativer Ansatz:

\(f(x) = \frac{p(x)}{q(x)}\), wobei \(p(x)\) und \(q(x)\) Polynome gleichen Grades sind und die Polynomdivision von p(x) durch q(x) den Funktionsterm in die Form \(f(x) = 2 \pm g(x)\) mit \(\lim \limits_{x \, \to \, \pm \infty} g(x) = 0\) überführt.

\(\Longrightarrow \quad\) z.B. \(\displaystyle f(x) = \frac{2x^2}{(x + 1)^2} = 2 - \frac{4x +2}{(x + 1)^2}\)

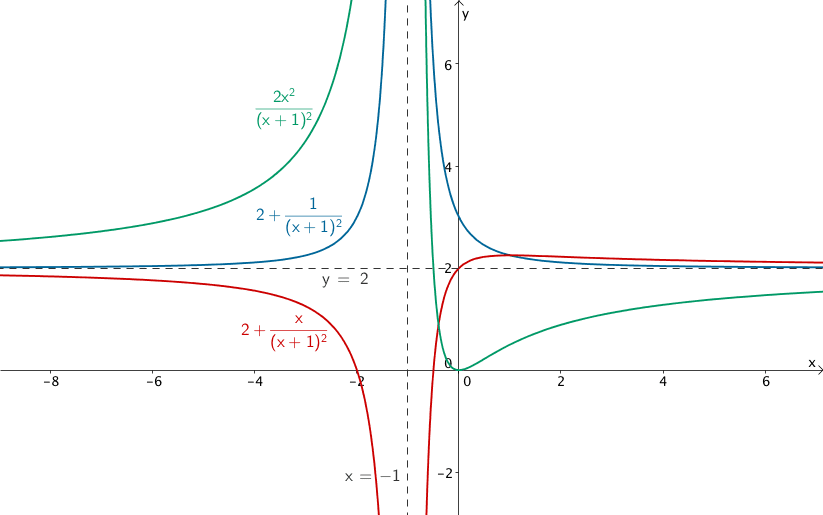
Beispiele für gebrochen-rationale Funktionen, deren Graph in \(x = -1\) eine Polstelle ohne Vorzeichenwechsel hat, und die waagrechte Asymptote \(y = 2\) besitzt.