Gegeben sind die Ebene \(E \colon 2x_{1} + x_{2} + 2x_{3} = 6\) sowie die Punkte \(P(1|0|2)\) und \(Q(5|2|6)\).
Zeigen Sie, dass die Gerade durch die Punkte \(P\) und \(Q\) senkrecht zur Ebene \(E\) verläuft.
(2 BE)
Lösung zu Teilaufgabe 1a
Lineare Abhängigkeit von Vektoren
\[E \colon 2x_{1} + x_{2} + 2x_{3} = 6\]
\(P(1|0|2)\), \(Q(5|2|6)\)
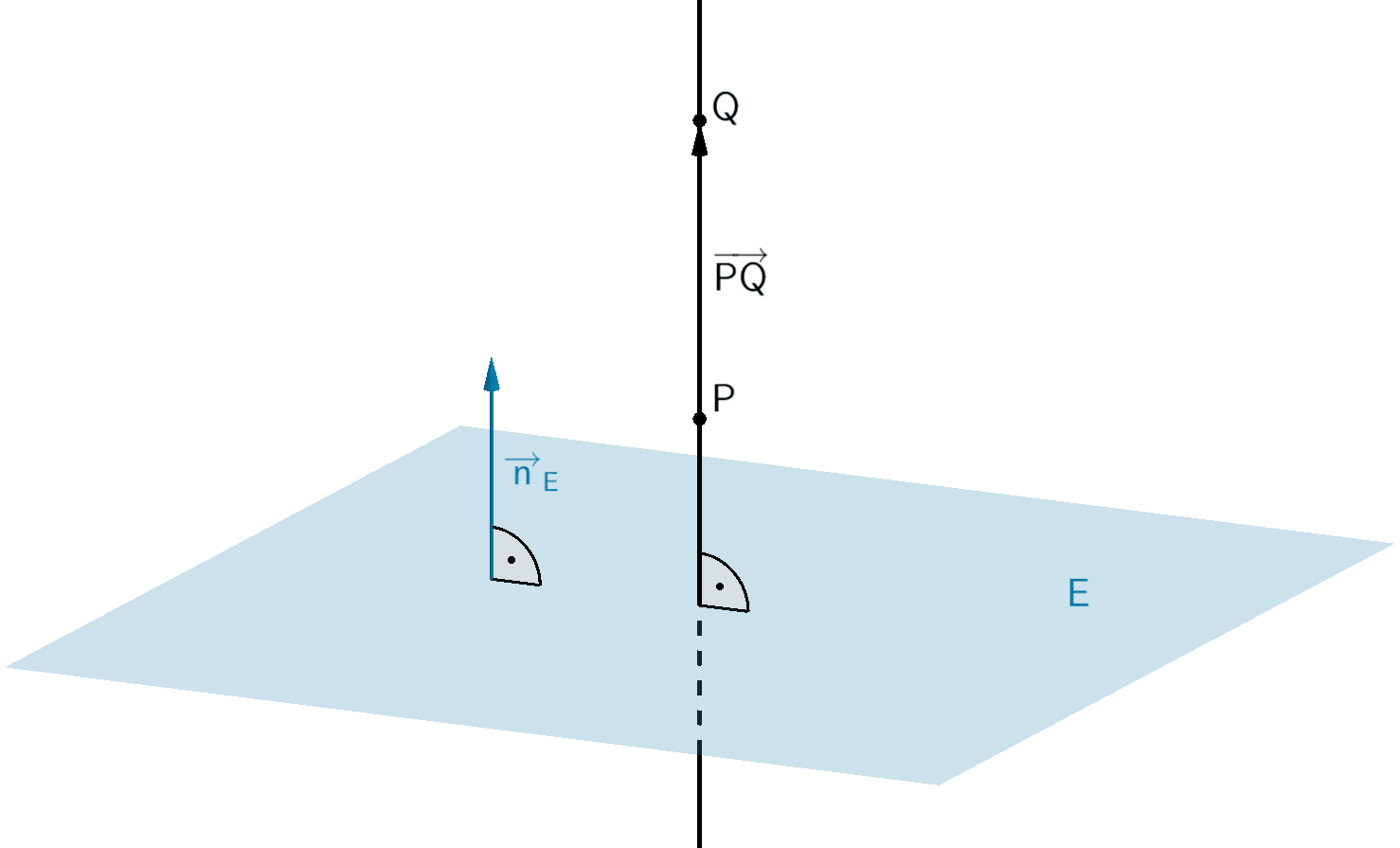
Planskizze: Ebene \(E\) und Gerade \(PQ \perp E\)
Die Gerade \(PQ\) durch die Punkte \(P\) und \(Q\) verläuft senkrecht zur Ebene \(E\), wenn der Verbindungsvektor \(\overrightarrow{PQ}\) (oder \(\overrightarrow{QP}\)) und der Noramlenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) linear abhängig sind. Das heißt, es muss beispielsweise gelten:
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\(\overrightarrow{PQ} = k \cdot \overrightarrow{n}_{E}; \; k \in \mathbb R\)
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\):
Der Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) kann der Ebenengleichung entnommen werden.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
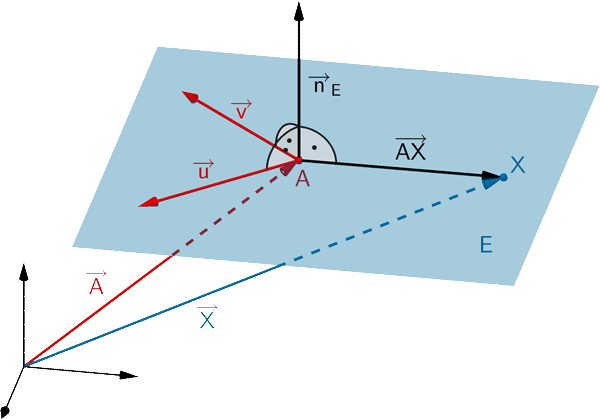
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon 2x_{1} + x_{2} + 2x_{3} = 6 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\]
Verbindungsvektor \(\overrightarrow{PQ}\) bestimmen:
\(P(1|0|2)\), \(Q(5|2|6)\)
\[\overrightarrow{PQ} = \overrightarrow{Q} - \overrightarrow{P} = \begin{pmatrix} 5 \\ 2 \\ 6 \end{pmatrix} - \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \\ 4 \end{pmatrix}\]
Lineare Abhängigkeit der Vektoren \(\overrightarrow{PQ}\) und \(\overrightarrow{n}_{E}\) prüfen:
\[\overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}; \enspace \overrightarrow{PQ} = \begin{pmatrix} 4 \\ 2 \\ 4 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{PQ} = 2 \cdot \overrightarrow{n}_{E}\]
Die Vektoren \(\overrightarrow{PQ}\) und \(\overrightarrow{n}_{E}\) sind linear abhängig. Folglich verläuft die Gerade \(PQ\) senkrecht zur Ebene \(E\).
