Begründen oder widerlegen Sie folgende Aussage:
Wenn der Graph \(G_f\) einer gebrochenrationalen Funktion \(f\) punktsymmetrisch zum Koordinatenursprung ist, so hat \(f\) mindestens zwei Definitionslücken.
Die Aussage ist falsch!
Widerlegung der Aussage durch ein Gegenbeispiel
1. Gegenbeispiel
Die Funktion \(f \colon x \mapsto \dfrac{1}{x}\) hat nur eine Definitionslücke \(x = 0\) und ihr Graph ist punktsymmetrisch zum Koordinatenursprung, denn es gilt:
\[f(-x) = \frac{1}{-x} = -\frac{1}{x} =-f(x)\]
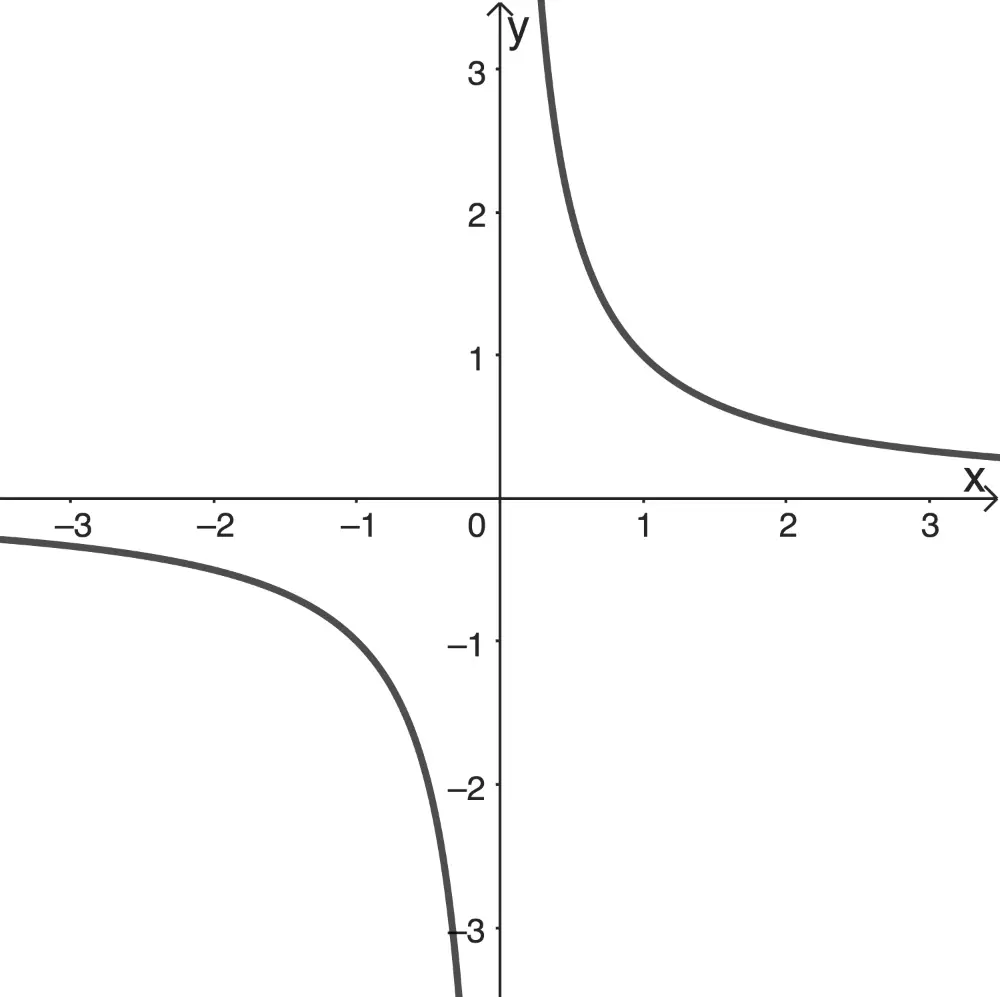
Graph der Funktion \(f \colon x \mapsto \dfrac{1}{x}\) mit \(D_f = \mathbb R \backslash \{0\}\) (ergänzende Zeichnung)
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
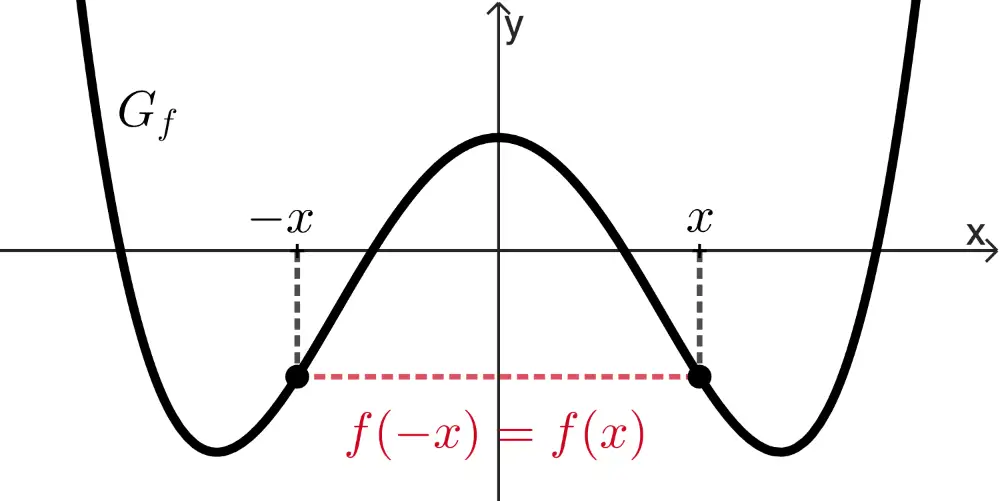
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
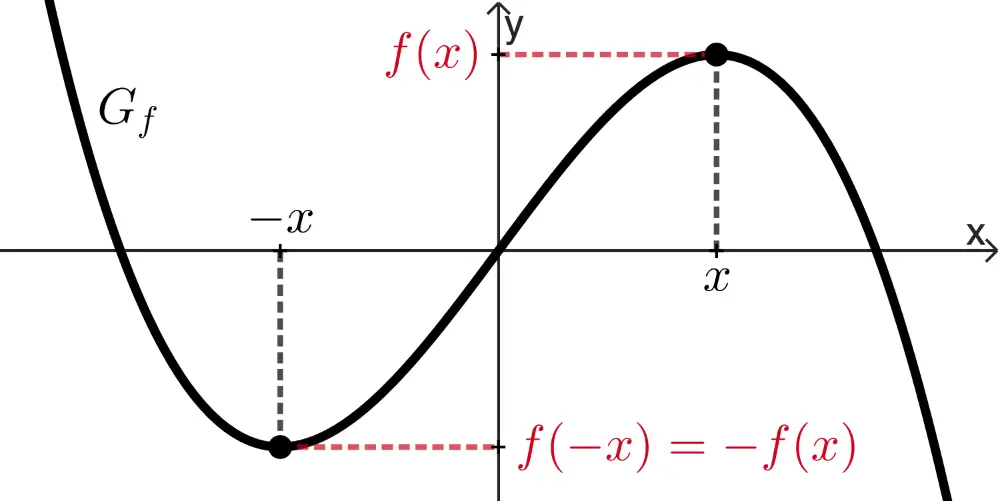
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
2. Gegenbeispiel
Die Funktion \(f \colon x \mapsto \dfrac{x}{x^2+1}\) ist in \(\mathbb R\) definiert (hat keine Definitionslücke) und ihr Graph ist punktsymmetrisch zum Koordinatenursprung, denn es gilt:
\[f(-x) = \frac{-x}{(-x)^2+1} = -\frac{x}{x^2+1} = -f(x)\]
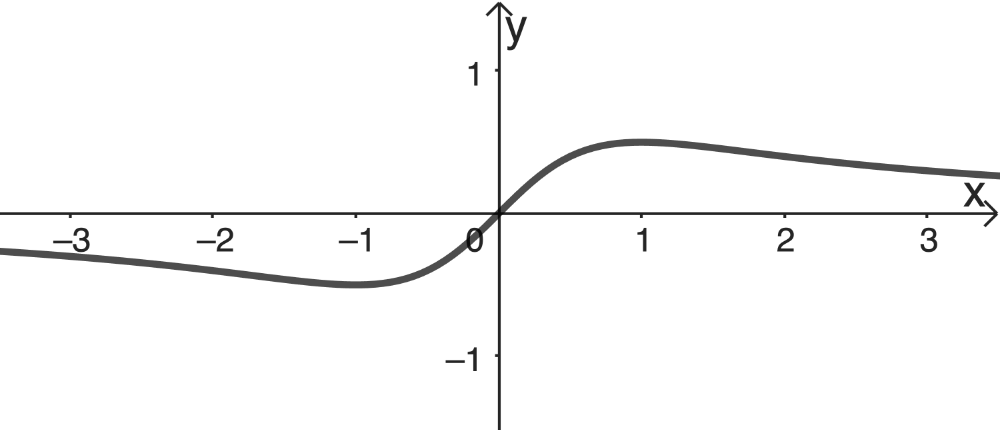
Graph der Funktion \(f \colon x \mapsto \dfrac{x}{x^2+1}\) mit \(D_f = \mathbb R\) (ergänzende Zeichnung)


