Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = \frac{1}{8}x^{3}\) sowie die Punkte \(Q_{a}(a|f(a))\) für \(a \in \mathbb R\). Die Abbildung zeigt den Graphen von \(f\) sowie die Punkte \(P(0|2)\) und \(Q_{2}\).
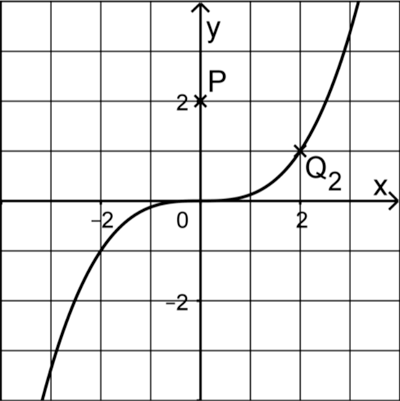
Berechnen Sie für \(a \neq 0\) die Steigung \(m_{a}\) der Gerade durch die Punkte \(P\) und \(Q_{a}\) in Abhängigkeit von \(a\).
(zur Kontrolle: \(m_{a} = \dfrac{a^{3} - 16}{8a}\))
(2 BE)
Lösung zu Teilaufgabe 4a
\[f(x) = \frac{1}{8}x^{3}; \; D_{f} = \mathbb R\]
\(P(0|2)\)
\(Q_{a}(a|f(a))\) mit \(a \in \mathbb R\)
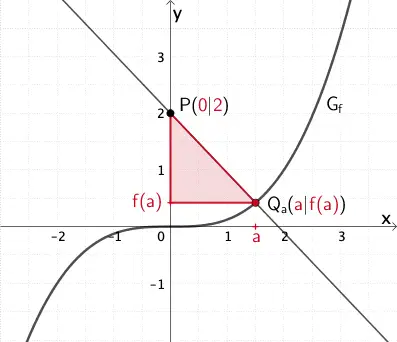
Mithilfe eines Steigungsdreiecks ergibt sich die Steigung \(m_{a}\) der Gerade durch die Punkte \(P(\textcolor{#cc071e}{0}|\textcolor{#cc071e}{2})\) und \(Q_{a}(\textcolor{#cc071e}{a}|\textcolor{#cc071e}{f(a)})\) in Abhängigkeit von \(a\) (\(a \neq 0\)) wie folgt:
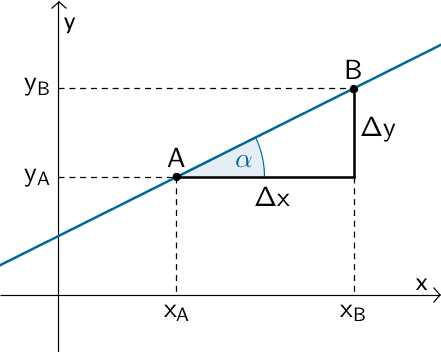
Steigung \(m\) einer Gerade
\[m = \frac{\Delta y}{\Delta x} = \frac{y_B - y_A}{x_B - x_A}\]
\[m = \tan \alpha \quad (\alpha \neq 90^{\circ})\]
\[\begin{align*} m_{a} &= \frac{\textcolor{#cc071e}{\Delta y}}{\textcolor{#cc071e}{\Delta x}} = \frac{\textcolor{#cc071e}{y_{Q_{a}} - y_{P}}}{\textcolor{#cc071e}{x_{Q_{a}} - x_{P}}} = \frac{\textcolor{#cc071e}{f(a) - 2}}{\textcolor{#cc071e}{a - 0}} \\[0.8em] &= \frac{\frac{1}{8}a^{3} - 2}{a} = \frac{\frac{1}{8}(a^{3} - 16)}{a} \\[0.8em] &= \frac{a^{3} - 16}{8a}\end{align*}\]


