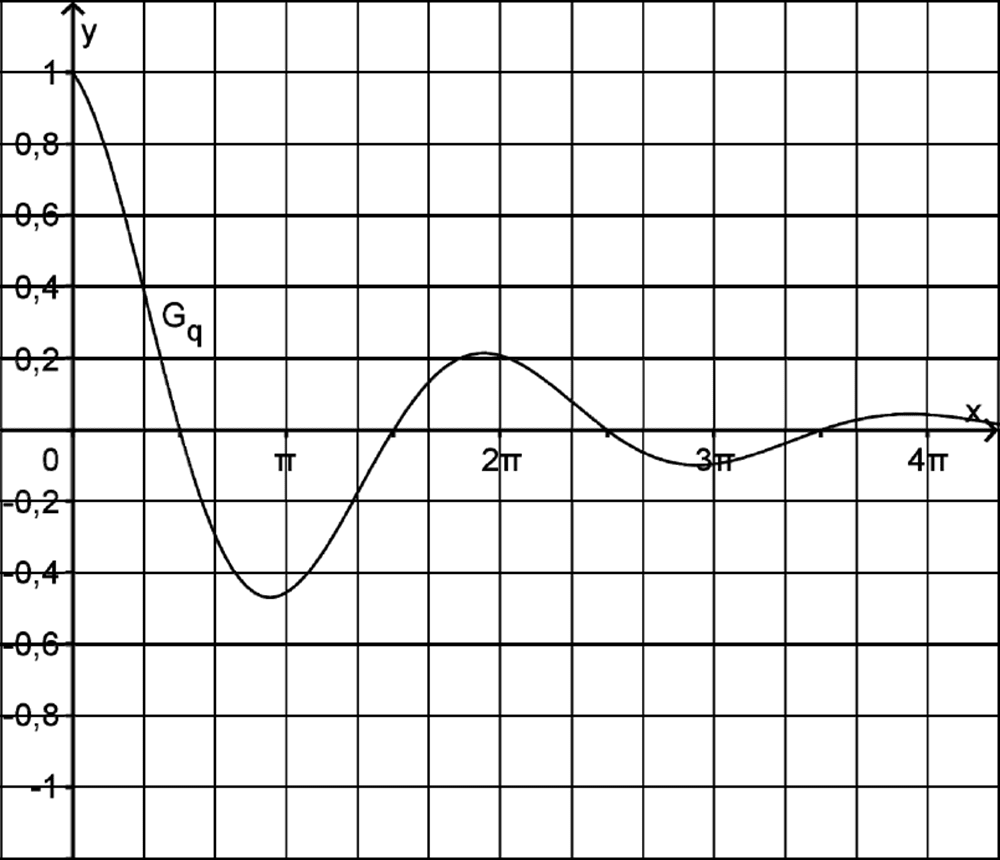
Gegeben sind die in \(\mathbb R\) definierten Funktionen \(p\,\colon x \mapsto e^{-\frac{1}{4}x}\) und \(q\,\colon x \mapsto e^{-\frac{1}{4}x} \cdot \cos x\). Die Abbildung zeigt den Graphen \(G_q\) von \(q\) füe \(x \geq 0\).
Untersuchen Sie das Monotonieverhalten des Graphen von \(p\) und geben Sie das Verhalten von \(p\) für \(x \to +\infty\) und \(x \to -\infty\) an.
(4 BE)
Lösung zu Teilaufgabe 2a
\[p(x) = e^{-\frac{1}{4}x}\,; \quad D = \mathbb R\]
Monotonieverhalten des Graphen von \(p\)
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Erste Ableitung \(p'\) bilden:
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der natürlichen Exponentialfunktion
\[f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
(vgl. Merkhilfe)
\[\begin{align*}p(x) = e^{-\frac{1}{4}x} \quad \Longrightarrow \quad p'(x) &= e^{-\frac{1}{4}x} \cdot \left ( -\frac{1}{4} \right ) \\[0.8em] &= -\frac{1}{4}e^{-\frac{1}{4}x}\end{align*}\]
Monotoniekriterium anwenden:
\[p'(x) = -\frac{1}{4} \underbrace{e^{-\frac{1}{4}x}}_{> 0}\]
\(\Longrightarrow \quad p'(x) < 0\) für alle \(x \in \mathbb R\)
\(\Longrightarrow \quad\) Der Graph von \(p\) ist für alle \(x \in \mathbb R\) streng monoton fallend.
Verhalten von \(p\) für \(x \to +\infty\) und \(x \to -\infty\)
\[\lim \limits_{x \to +\infty} p(x) = \lim \limits_{x \to +\infty} e^{-\frac{1}{4}x} = \lim \limits_{x\,\to\,+\infty}\; \frac{1}{e^{\frac{1}{4}x}} = 0\]
\[\lim \limits_{x \to -\infty} p(x) = \lim \limits_{x \to -\infty} e^{-\frac{1}{4}x} = +\infty\]

