Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto x \cdot e^{4 - 0{,}25x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Überprüfen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
b) Bestimmen Sie die Nullstelle(n) von \(f\) sowie die Lage und Art des/der Extrempunkte(s) von \(G_{f}\).
c) Ermitteln Sie die Gleichung der Normale \(N\) im Punkt P\((0|f(0))\).
a) Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems
Man bestimmt den Funktionsterm \(f(-x)\). Gilt \(f(-x) = f(x)\), ist \(G_{f}\) achsensymmetrisch zur \(y\)-Achse. Gilt \(f(-x) = -f(x)\), ist \(G_{f}\) punktsymmetrisch zum Koordinatenursprung \(O(0|0)\). Trifft keiner der beiden Fälle zu, weist \(G_{f}\) keines der beiden Symmetrieverhalten auf.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
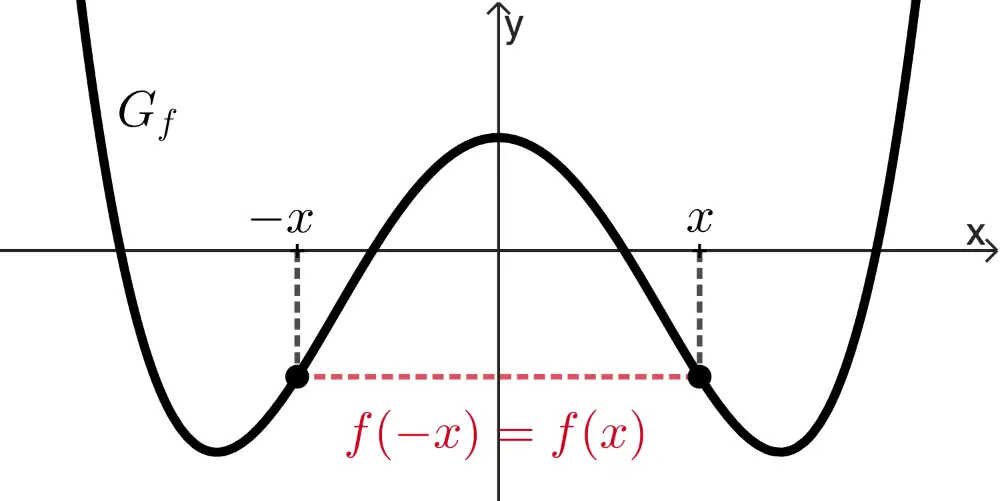
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
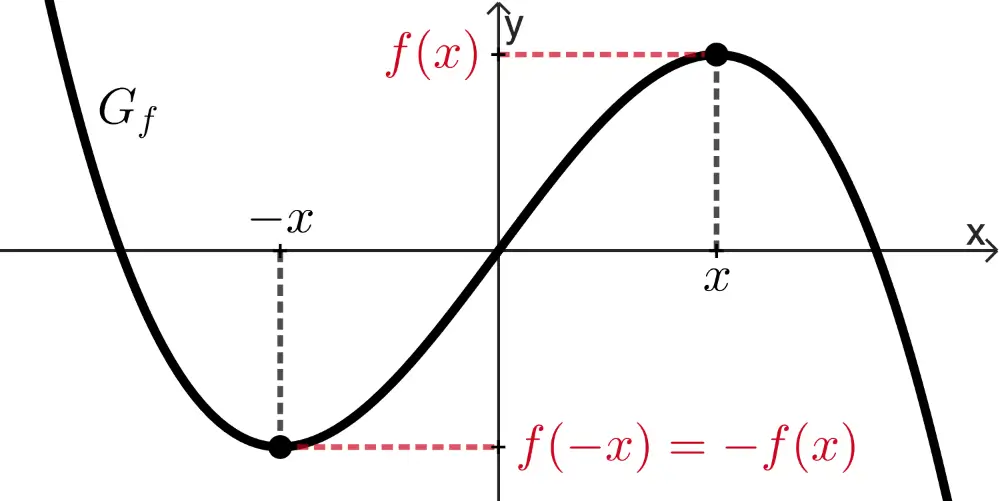
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(x) = x \cdot e^{4 - 0{,}25x^{2}}; \; D_{f} = \mathbb R\]
\[\begin{align*} f(-x) &= (-x) \cdot e^{4 - 0{,}25 \cdot (-x)^{2}} \\[0.8em] &= -x \cdot e^{4 - 0{,}25x^{2}} \\[0.8em] &= -f(x) \end{align*}\]
\(\Longrightarrow \quad G_{f}\) ist punktsymmetrisch zum Koordinatenursprung \(O(0|0)\).
b) Nullstelle(n) von \(f\) sowie die Lage und Art des/der Extrempunkte(s) von \(G_{f}\)
Nullstelle(n) der Funktion \(f\)
Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
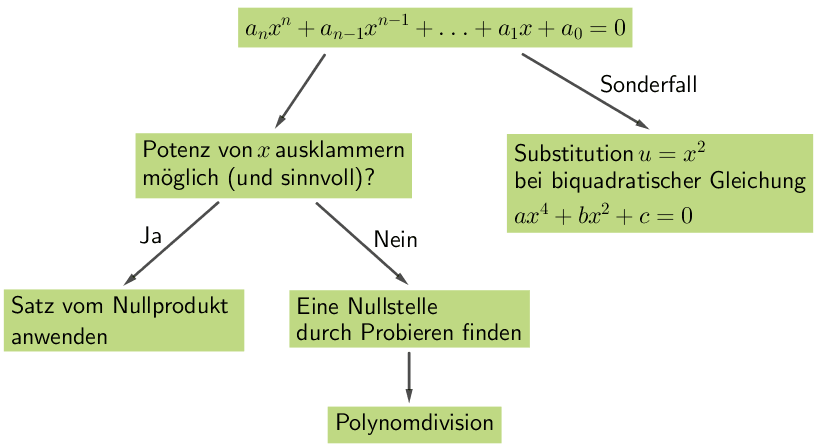
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[\begin{align*}f(x) &= 0 \\[0.8em] x \cdot \underbrace{e^{4 - 0{,}25x^{2}}}_{>\,0} &= 0 \\[0.8em] \Longrightarrow \quad x &= 0\end{align*}\]
\(x = 0\) ist einzige Nullstelle der Funktion \(f\).
Lage und Art des/der Extrempunkte(s) von \(G_{f}\)
An den Extremstellen besitzt der Graph der Funktion \(f\) eine waagrechte Tangente, das heißt, die Tangentensteigung ist gleich Null. Die erste Ableitung \(f'\) der Funktion \(f\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\),
Folglich lautet die notwendige Bedingung für einen Extrempunkt von \(G_{f}\):
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = 0\]
Erste Ableitung \(f'\) bilden:
Die erste Ableitung \(f'\) der Funktion \(f\) wird mithilfe der Produktregel, der Kettenregel, der Ableitung der natürlichen Exponentialfunktion, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel gebildet.
\[f(x) = x \cdot e^{4 - 0{,}25x^{2}}; \; D_{f} = \mathbb R\]
Produktregel
\[f(x) = u(x) \cdot v(x) \quad \Longrightarrow \quad f'(x) = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
Kettenregel
\[f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung der natürlichen Exponentialfunktion
\[ f(x) = e^x \quad \Longrightarrow \quad f'(x) = e^x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left[u(x) \cdot v(x)\right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]
\[u(x) = x); \; u'(x) = 1\]
\[\begin{align*}v(x) = e^{4 - 0{,}25x^{2}}; \; v'(x) &= e^{4 - 0{,}25x^{2}} \cdot (0 - 0{,}25 \cdot 2x) \\[0.8em] &= -0{,}5xe^{4 - 0{,}25x^{2}}\end{align*}\]
\[\begin{align*} f'(x) &= 1 \cdot e^{4 - 0{,}25x^{2}} + x \cdot \left( -0{,}5xe^{4 - 0{,}25x^{2}} \right) \\[0.8em] &= e^{4 - 0{,}25x^{2}} - 0{,}5x^{2}e^{4 - 0{,}25x^{2}} \\[0.8em] &= e^{4 - 0{,}25x^{2}} \cdot \left( 1 - 0{,}5x^{2} \right) \\[0.8em] &= 0{,}5e^{4 - 0{,}25x^{2}} \cdot \left( 2 - x^{2} \right) \end{align*}\]
Nullstellen von \(f'\) berechnen:
\[\begin{align*}f'(x) &= 0 \\[0.8em] \underbrace{0{,}5e^{4 - 0{,}25x^{2}}}_{>\,0} \cdot \left( 2 - x^{2} \right) &= 0\end{align*}\]
\[\begin{align*}\Longrightarrow \quad 2 - x^{2} &= 0 & &| + x^{2} \\[0.8em] 2 &= x^{2} & &| \; \sqrt{\quad} \\[0.8em] \pm \sqrt{2} &= x_{1,2} \end{align*}\]
An den Stellen \(x_{1} = -\sqrt{2}\) und \(x_{2} = \sqrt{2}\) besitzt der Graph der Funktion \(f\) eine waagrechte Tangente, welche auf einen Extrempunkt (bzw. einen Terrassenpunkt) hinweist.
Nachweis der Art der Extrempunkte:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = \underbrace{0{,}5e^{4 - 0{,}25x^{2}}}_{>\,0} \cdot \left( 2 - x^{2} \right)\]
Der Faktor \((2 - x^{2})\) bestimmt den Vorzeichenwechsel von \(f'\) in der Umgebung der Stellen \(x_{1} = -\sqrt{2}\) und \(x_{2} = \sqrt{2}\).
\((2 - x^{2}) < 0\) für \(x < -\sqrt{2}\) bzw. \(x > 2\)
\((2 - x^{2}) > 0\) für \(x > -\sqrt{2}\) bzw. \(x < 2\)
Somit ergibt sich:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &f'(x) < 0 \; \text{für} \; x < -\sqrt{2} \\[0.8em] &f'(-\sqrt{2}) = 0 \\[0.8em] &f'(x) > 0 \; \text{für} \; x > -\sqrt{2} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt} \; TiP\big(-\sqrt{2} \big|f(-\sqrt{2}) \big)\]
\[\left. \begin{align*} &f'(x) > 0 \; \text{für} \; x < \sqrt{2} \\[0.8em] &f'(\sqrt{2}) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; x > \sqrt{2} \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt} \; HoP\big(\sqrt{2} \big|f(\sqrt{2}) \big)\]
Veranschaulichung mit einer Monotonietabelle:
\[f'(x) = \underbrace{0{,}5e^{4 - 0{,}25x^{2}}}_{>\,0} \cdot \left( 2 - x^{2} \right)\]
| \(x\) | \(x < -\sqrt{2}\) | \(x = -\sqrt{2}\) | \(x > -\sqrt{2}\) |
| \(0{,}5e^{4 - 0{,}25x^{2}}\) | \(+\) | \(+\) | \(+\) |
| \((2 - x^{2})\) | \(-\) | \(0\) | \(+\) |
| \(f'(x)\) | \(-\) | \(+\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP \big(-\sqrt{2} \big| f(-\sqrt{2}) \big)\) | \(\nearrow\) |
| \(x\) | \(x < \sqrt{2}\) | \(x = \sqrt{2}\) | \(x > \sqrt{2}\) |
| \(0{,}5e^{4 - 0{,}25x^{2}}\) | \(+\) | \(+\) | \(+\) |
| \((2 - x^{2})\) | \(+\) | \(0\) | \(-\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\nearrow\) | \(HoP \big( \sqrt{2} \big| f(\sqrt{2}) \big)\) | \(\searrow\) |
\(y\)-Koordinate der Extrempunkte berechnen:
\[f(x) = x \cdot e^{4 - 0{,}25x^{2}}; \; D_{f} = \mathbb R\]
\[f(-\sqrt{2}) = -\sqrt{2} \cdot e^{4 - 0{,}25 \cdot (-\sqrt{2})^{2}} = -\sqrt{2}e^{3{,}5}\]
\[\Longrightarrow \quad TiP\big( -\sqrt{2} \big| -\sqrt{2}e^{3{,}5} \big)\]
\[f(\sqrt{2}) = \sqrt{2} \cdot e^{4 - 0{,}25 \cdot {\sqrt{2}}^{2}} = \sqrt{2}e^{3{,}5}\]
\[\Longrightarrow \quad HoP\big( \sqrt{2} \big| \sqrt{2}e^{3{,}5} \big)\]
Anmerkung:
Es ist ebenso möglich, zunächst die Lage und Art von nur einem der beiden Extrempunkte zu bestimmen und anschließend aufgrund der in Teilaufgabe a festgestellten Punktsymmetrie zum Koordinatenursprung von \(f\) auf die Lage und Art des jeweils anderen Extrempunkts zu schließen.
c) Gleichung der Normale \(N\) im Punkt P\((0|f(0))\)
\(x = 0\) ist Nullstelle der Funktion \(f\) (vgl. Teilaufgabe b).
\[\Longrightarrow \quad P(0|0)\]
Die Normale \(N\) durch den Punkt \(P(0|0)\) (Koordinatenursprung) ist eine Ursprungsgerade. Der Ansatz erfolgt mit der Gleichung einer Ursprungsgeraden \(y = mx\).
\[N \colon y = m_{N} \cdot x\]
Steigung \(m_{N}\) der Normalen \(N\) bestimmen:
Anwendung der Differetialrechnung:
Tangentensteigung und Normalensteigung
Tangentensteigung: \(m_{T} = f'(x_0)\)
Normalensteigung: \(m_{N} = -\dfrac{1}{f'(x_0)}\)
(vgl. Merkhilfe)
Zwischen der Steigung \(m_{N}\) der Normalen \(N\) und der Steigung \(m_{T}\) der Tangente an \(G_{f}\) im Punkt \(P\) gilt:
\[m_{N} = -\frac{1}{m_{T}}\]
Die erste Ableitung der Funktion \(f\) an der Stelle \(x = 0\) beschreibt die Steigung \(m_{T}\) der Tangente \(T\) an \(G_{f}\) im Punkt \(P\).
\[m_{N} = -\frac{1}{m_{T}} = \frac{1}{f'(0)}\]
Die erste Ableitung \(f'\) ist aus Teilaufgabe b bereits bekannt:
\[f'(x) = 0{,}5e^{4 - 0{,}25x^{2}} \cdot \left( 2 - x^{2} \right)\]
Steigung \(m_{N}\) der Normalen \(N\) berechnen:
\[\begin{align*}m_{N} &= -\frac{1}{f'(0)} \\[0.8em] &= -\frac{1}{0{,}5e^{4 - 0{,}25 \cdot 0^{2}} \cdot (2 - 0^{2})} \\[0.8em] &= -\frac{1}{e^{4}}\end{align*}\]
Gleichung der Normalen \(N\) angeben:
\[N \colon y = -\frac{1}{e^{4}}x\]

