Mathematik Klausur Q11/1-003 Bayern
Aufgabe 1
Geben Sie eine gebrochenrationale Funktion \(f\) an, deren Graph die Asymptote mit der Gleichung \(y = 2x - 1\) sowie die Nullstelle \(x = 2\) besitzt.
Aufgabe 2
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{4x + 4}{x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie die maximale Definitionsmenge sowie die Nullstelle(n) und die Polstelle(n) der Funktion \(f\) an. Bestimmen Sie die Gleichungen aller Asymptoten des Graphen der Funktion \(f\).
b) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
c) Leiten Sie die Funktion \(f\) sowohl mit der Produkt- als auch der Quotientenregel ab.
(Zur Kontrolle: \(f'(x) = \dfrac{-4x - 8}{x^{3}}\))
d) Bestimmen Sie die Nullstelle(n) der Ableitungsfunktion und deuten Sie das Ergebnis geometrisch.
e) Ermitteln Sie die Gleichung der Tangente \(T\) an \(G_{f}\) an der Stelle \(x = 2\).
Aufgabe 3
a) Berechnen Sie die Ableitung folgender Funktionen mithilfe der Ableitungsregeln ohne anschließend zu vereinfachen.
α) \(f(x) = 3x^{4} - \dfrac{3}{x} + 6\)
β) \(g(x) = (2x - 3)(x^{2} - t)\)
γ) \(h(x) = \dfrac{3x - 5}{3 - x^{3}}\)
b) Bestimmen Sie eine Stammfunktion der Funktion \(f \colon x \mapsto 3x^{4} + \dfrac{3}{x^{3}} - 4\).
Aufgabe 4
Gegeben ist die Funktion \(f \colon x \mapsto 4x^{2} - 1\).
a) Bestimmen Sie die mittlere Änderungsrate auf dem Intervall \([1;3]\).
b) Bestimmen Sie \(f'(2)\) unter Verwendung des Differentialquotienten.
Aufgabe 5
Florian behauptet: „Sind die Ableitungen von zwei Funktionen gleich, so sind auch die Funktionen selbst gleich."
Nehmen Sie zu Florians Aussage begründend Stellung.
Aufgabe 6
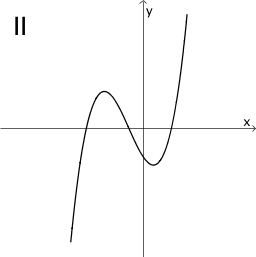
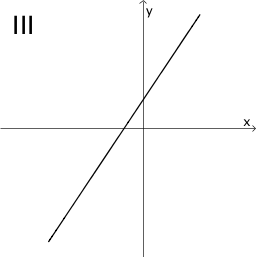
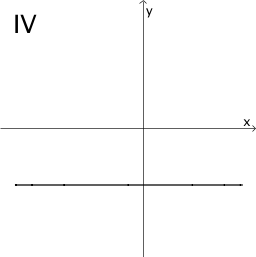
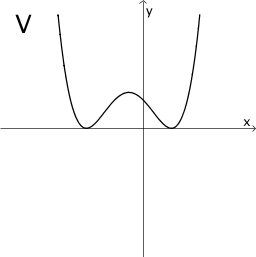
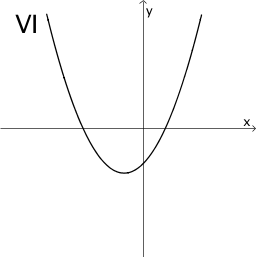
Ordnen Sie die Graphen I bis VI den freien Feldern der Tabelle so zu, dass unter einem Funktionsgraphen jeweils der Graph seiner Ableitung zu sehen ist und beschriften Sie die Felder entsprechend. Begründen Sie Ihre Wahl für die erste Spalte.
Hinweis: Die Skalierung der Koordinatenachsen ist für alle abgebildeten Graphen dieselbe.
 |
||
 |
||
 |
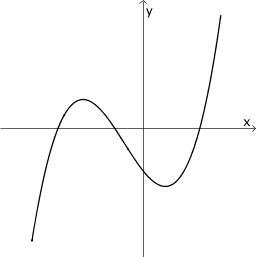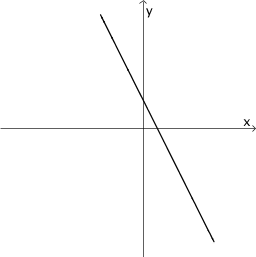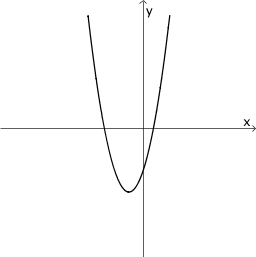Graphen I bis VI:
 |
 |
 |
 |
 |
 |
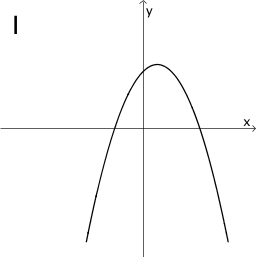- Details
- Hauptkategorie: Klausuren Q11/1
Geben Sie eine gebrochenrationale Funktion \(f\) an, deren Graph die Asymptote mit der Gleichung \(y = 2x - 1\) sowie die Nullstelle \(x = 2\) besitzt.
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{4x + 4}{x^{2}}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Geben Sie die maximale Definitionsmenge sowie die Nullstelle(n) und die Polstelle(n) der Funktion \(f\) an. Bestimmen Sie die Gleichungen aller Asymptoten des Graphen der Funktion \(f\).
b) Untersuchen Sie das Symmetrieverhalten von \(G_{f}\) bezüglich des Koordinatensystems.
c) Leiten Sie die Funktion \(f\) sowohl mit der Produkt- als auch der Quotientenregel ab.
(Zur Kontrolle: \(f'(x) = \dfrac{-4x - 8}{x^{3}}\))
d) Bestimmen Sie die Nullstelle(n) der Ableitungsfunktion und deuten Sie das Ergebnis geometrisch.
e) Ermitteln Sie die Gleichung der Tangente \(T\) an \(G_{f}\) an der Stelle \(x = 2\).
- Details
- Hauptkategorie: Klausuren Q11/1
a) Berechnen Sie die Ableitung folgender Funktionen mithilfe der Ableitungsregeln ohne anschließend zu vereinfachen.
α) \(f(x) = 3x^{4} - \dfrac{3}{x} + 6\)
β) \(g(x) = (2x - 3)(x^{2} - t)\)
γ) \(h(x) = \dfrac{3x - 5}{3 - x^{3}}\)
b) Bestimmen Sie eine Stammfunktion der Funktion \(f \colon x \mapsto 3x^{4} + \dfrac{3}{x^{3}} - 4\).
- Details
- Hauptkategorie: Klausuren Q11/1
Gegeben ist die Funktion \(f \colon x \mapsto 4x^{2} - 1\).
a) Bestimmen Sie die mittlere Änderungsrate auf dem Intervall \([1;3]\).
b) Bestimmen Sie \(f'(2)\) unter Verwendung des Differentialquotienten.
- Details
- Hauptkategorie: Klausuren Q11/1
Florian behauptet: „Sind die Ableitungen von zwei Funktionen gleich, so sind auch die Funktionen selbst gleich."
Nehmen Sie zu Florians Aussage begründend Stellung.
- Details
- Hauptkategorie: Klausuren Q11/1
Ordnen Sie die Graphen I bis VI den freien Feldern der Tabelle so zu, dass unter einem Funktionsgraphen jeweils der Graph seiner Ableitung zu sehen ist und beschriften Sie die Felder entsprechend. Begründen Sie Ihre Wahl für die erste Spalte.
Hinweis: Die Skalierung der Koordinatenachsen ist für alle abgebildeten Graphen dieselbe.
|
||
| |
||
| |
Graphen I bis VI:
|
|
|
|
|
|
- Details
- Hauptkategorie: Klausuren Q11/1
2023 Christian Rieger・mathelike
