Gegeben ist die Gerade \(g\) mit der Gleichung \(g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 6 \\ -3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 2 \\ -3 \end{pmatrix}; \; \lambda \in \mathbb R\) sowie die Kugel \(K\) mit dem Mittelpunkt \(M(3|4|5)\) und dem Radius \(r = 3\).
Zeigen Sie durch Rechnung, dass die Gerade \(g\) die Kugel \(K\) tangiert.
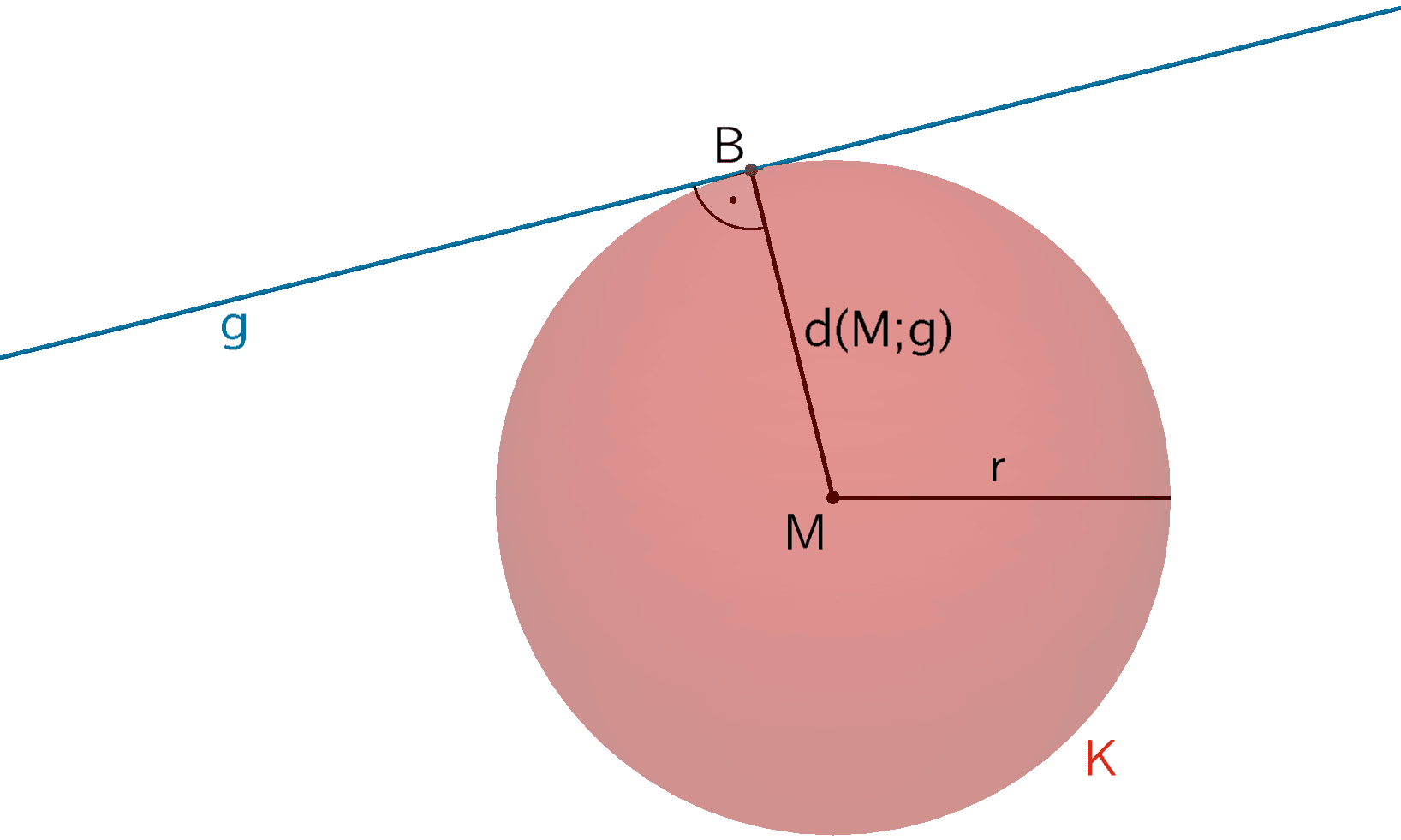
Die Gerade \(g\) berührt (tangiert) die Kugel \(K\), wenn der Abstand \(d(M;g)\) des Mittelpunkts \(M\) von der Geraden \(g\) gleich dem Radius \(r\) ist (vgl. Abiturskript - 2.7.3 Lagebeziehung Gerade - Kugel).
Anstatt nun relativ aufwendig den Abstand \(d(M;g)\) zu berechnen (vgl. Abiturskript - 2.4.1 Abstand Punkt - Gerade), ist es einfacher, den Ansatz für die Berechnung der gemeinsamen Punkte der Kugel \(K\) und der Geraden \(g\) zu wählen.
Gleichung der Kugel \(K\) formulieren:
\(M(3|4|5)\), \(r = 3\)
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[K \colon (x_{1} - 3)^{2} + (x_{2} - 4)^{2} + (x_{3} - 5)^{2} = 9\]
Für die Berechnung der gemeinsamen Punkte der Kugel \(K\) und der Geraden \(g\) werden die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Geraden \(g\) in die Kugelgleichung eingesetzt. Es ergibt sich eine quadratische Gleichung für den Parameter \(\lambda\), welche im Falle eines Berührpunkts genau eine Lösung hat.
\[g \colon \overrightarrow{X} = \begin{pmatrix} 6 \\ 6 \\ -3 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 2 \\ -3 \end{pmatrix} = \begin{pmatrix} 6 + 2\lambda \\ 6 + 2\lambda \\ -3 - 3\lambda \end{pmatrix}; \; \lambda \in \mathbb R\]
\[\begin{align*} g \cap K \colon (6 + 2\lambda - 3)^{2} + (6 + 2\lambda - 4)^{2} + (-3 - 3\lambda - 5)^{2} &= 9 \\[0.8em] (3 + 2\lambda)^{2} + (2 + 2\lambda)^{2} + (-8 - 3\lambda)^{2} &= 9 \\[0.8em] 9 + 12\lambda + 4\lambda^{2} + 4 + 8\lambda + 4\lambda^{2} + 64 + 48\lambda + 9\lambda^{2} &= 9 \\[0.8em] 17\lambda^{2} + 68\lambda + 77 &= 9 &&| - 9 \\[0.8em] 17\lambda^{2} + 68\lambda + 68 &= 0 \end{align*}\]
Die quadratische Gleichung hat genau eine Lösung, wenn die Diskriminante \(D\) gleich Null ist.
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[17\lambda^{2} + 68\lambda + 68 = 0 \quad \Longrightarrow \quad a = 17, \; b = 68, \; c = 68\]
\[D = b^{2} - 4ac = 68^{2} - 4 \cdot 17 \cdot 68 = 0\]
Also existiert genau ein gemeinsamer Punkt der Kugel \(K\) und der Gerade \(g\) (Berührpunkt). Folglich tangiert die Gerade \(g\) die Kugel \(K\).

