Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto -\dfrac{1}{8}x^{3} + \dfrac{3}{2}x^{2} - \dfrac{9}{2}x\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
Untersuchen Sie das Monotonieverhalten der Funktion \(f\) und geben Sie die Lage und die Art der lokalen Extrempunkte von \(G_{f}\) an.
Die ganzrationale Funktion \(f\) ist in \(\mathbb R\) definiert.
\[f(x) = -\frac{1}{8}x^{3} + \frac{3}{2}x^{2} - \frac{9}{2}x; \, D_{f} = \mathbb R\]
Die Aufgabenstellung lässt offen, in welcher Reihenfolge das Monotonieverhalten der Funktion \(f\) und die Extrempunkte von \(G_{f}\) zu bestimmen sind. Es sind deshalb folgende zwei Lösungsansätze denkbar:
- 1. Von den Extrempunkten auf das Monotonieverhalten schließen
- 2. Vom Monotonieverhalten auf die Extrempunkte schließen
1. Lösungsansatz: Von den Extrempunkten auf das Monotonieverhalten schließen
An den Extremstellen wechselt der Graph der Funktion \(f\) das Monotonieverhalten. Deshalb wird zunächst die Lage der Extremstellen von \(G_{f}\) bestimmt. Die Monotonieintervalle der Funktion \(f\) ergeben sich dann durch den Nachweis der Art der Extrempunkte.
An den Extremstellen besitzt der Graph der Funktion \(f\) eine waagrechte Tangente, das heißt, die Tangentensteigung ist gleich Null. Die erste Ableitung \(f'\) der Funktion \(f\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(f\).
Folglich lautet die notwendige Bedingung für einen Extrempunkt von \(G_{f}\):
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[f'(x) = 0\]
Erste Ableitung \(f'\) bilden:
Die erste Ableitung \(f'\) der Funktion \(f\) kann mithilfe der Ableitung einer Potenzfunktion, der Summenregel und der Faktorregel formuliert werden.
\[f(x) = -\frac{1}{8}x^{3} + \frac{3}{2}x^{2} - \frac{9}{2}x\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*}f'(x) &= -\frac{1}{8} \cdot 3 \cdot x^{2} + \frac{3}{2} \cdot 2 \cdot x - \frac{9}{2} \\[0.8em] &= -\frac{3}{8}x^{2} + 3x - \frac{9}{2} \end{align*}\]
Nullstellen von \(f'\) berechnen:
\[\begin{align*} f'(x) = 0 \\[0.8em] -\frac{3}{8}x^{2} + 3x - \frac{9}{2} &= 0 & &| \cdot \left( -\frac{8}{3} \right) \\[0.8em] x^{2} - 8x + 12 &= 0 \end{align*}\]
Die quadratische Gleichung \(x^{2} - 8x + 12 = 0\) wird mit der Lösungsformel für quadratische Gleichungen gelöst.
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} x_{1,2} &= \frac{8 \pm \sqrt{(-8)^{2} - 4 \cdot 1 \cdot 12}}{2 \cdot 1} \\[0.8em] &= \frac{8 \pm 4}{2} \\[0.8em] &= 4 \pm 2 \end{align*}\]
\[x_{1} = 4 - 2 = 2\]
\[x_{2} = 4 + 2 = 6\]
An den Stellen \(x_{1} = 2\) und \(x_{2} = 6\) besitzt \(G_{f}\) jeweils eine waagrechte Tangente, welche auf einen Extrem- oder Terrassenpunkt hinweist.
Nachweis der Extrempunkte und deren Art:
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
Ein Extrempunkt liegt an den Stellen \(x_{1} = 2\) bzw. \(x_{2} = 6\) dann vor, wenn \(f'\) dort das Vorzeichen wechselt, das heißt, wenn \(G_{f}\) gemäß dem Monotoniekriterium das Monotonieverhalten ändert.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Um den Vorzeichenwechsel von \(f'\) besser beurteilen und dokumentieren zu können, ist es zweckmäßig, den Funktionsterm \(f'(x)\) als Produkt seiner Linearfaktoren zu beschreiben. Mithilfe der Nullstellen \(x_{1} = 2\) und \(x_{2} = 6\) von \(f'\) ergibt sich:
\[\begin{align*}f'(x) &= -\frac{3}{8}x^{2} + 3x - \frac{9}{2} \\[0.8em] &= -\frac{3}{8} \cdot (x^{2} - 8x + 12) & &| \; \text{Nullstellen:}\; x = 2; \; x = 6 \\[0.8em] &= -\frac{3}{8} \cdot (x - 2)(x - 6) \end{align*}\]
\[\left. \begin{align*} &f'(x) < 0 \; \text{für} \; x < 2 \\[0.8em] &f'(2) = 0 \\[0.8em] &f'(x) > 0 \; \text{für} \; 2 < x < 6 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\; TiP(2|f(2))\]
\[\left. \begin{align*} &f'(x) > 0 \; \text{für} \; 2 < x < 6 \\[0.8em] &f'(6) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; x > 6 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}\; HoP(6|f(6))\]
Monotonieverhalten der Funktion \(f\):
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(f'(x) < 0\) für \(x < 2 \quad \Longrightarrow \quad f\) ist im Intervall \(]-\infty;2[\) streng monoton fallend.
\(f'(x) > 0\) für \(2 < x < 6 \quad \Longrightarrow \quad f\) ist im Intervall \(]2;6[\) streng monoton steigend.
\(f'(x) < 0\) für \(x > 6 \quad \Longrightarrow \quad f\) ist im Intervall \(]6;+\infty[\) streng monoton fallend.
Lage (\(y\)-Koordinate) der Extrempunkte:
\[\begin{align*} f(2) &= -\frac{1}{8} \cdot 2^{3} + \frac{3}{2} \cdot 2^{2} - \frac{9}{2} \cdot 2 \\[0.8em] &= -1 + 6 - 9 \\[0.8em] &= -4\end{align*}\]
\[\Longrightarrow \quad TiP(2|-4)\]
\[\begin{align*} f(6) &= -\frac{1}{8} \cdot 6^{3} + \frac{3}{2} \cdot 6^{2} - \frac{9}{2} \cdot 6 \\[0.8em] &= -27 + 54 + 27 \\[0.8em] &= 0\end{align*}\]
\[\Longrightarrow \quad HoP(6|0)\]
Veranschaulichung mithilfe einer Monotonietabelle:
\[f'(x) = -\frac{3}{8} \cdot (x - 2)(x - 6)\]
| \(x\) | \(x < 2\) | \(2\) | \(2 < x < 6\) |
| \(-\frac{3}{8}\) | \(-\) | \(-\) | \(-\) |
| \((x - 2)\) | \(-\) | \(0\) | \(+\) |
| \((x - 6)\) | \(-\) | \(-\) | \(-\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(G_{f}\) | \(\searrow\) | \(TiP(2|-4)\) | \(\nearrow\) |
| \(x\) | \(2 < x < 6\) | \(6\) | \(x > 6\) |
| \(-\frac{3}{8}\) | \(-\) | \(-\) | \(-\) |
| \((x - 2)\) | \(+\) | \(+\) | \(+\) |
| \((x - 6)\) | \(-\) | \(0\) | \(+\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(G_{f}\) | \(\nearrow\) | \(HoP(6|0)\) | \(\searrow\) |
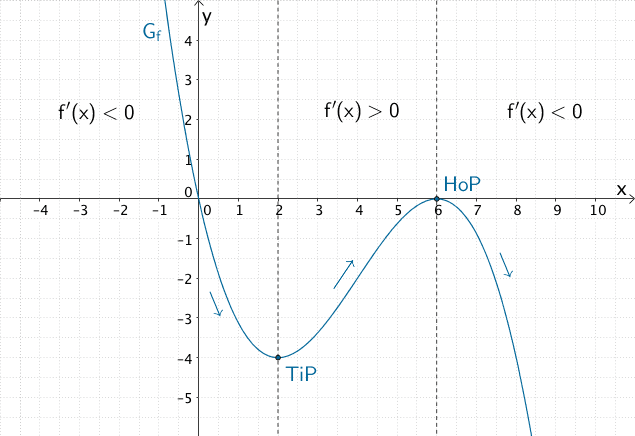
Graph der ganzrationalen Funktion \(f \colon x \mapsto -\dfrac{1}{8}x^{3} + \dfrac{3}{2}x^{2} - \dfrac{9}{2}x\), Monotonieverhalten der Funktion \(f\) und Extrempunkte von \(G_{f}\) (Zeichnung ist nicht Teil der Aufgabenstellung.)
2. Lösungsansatz: Vom Monotonieverhalten auf die Extrempunkte schließen
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Gemäß dem Monotoniekriterium gilt:
- \(f\) ist streng monoton fallend, falls \(f'(x) < 0\) gilt.
- \(f\) ist streng monoton steigend, falls \(f'(x) < 0\) gilt.
Es ist demnach die Gültigkeit der Ungleichungen \(f'(x) < 0\) und \(f'(x) > 0\) zu untersuchen.
Die erste Ableitung \(f'\) der Funktion \(f\) lautet (vgl. 1. Lösungsansatz):
\[f'(x) = -\frac{3}{8}x^{2} + 3x -\frac{9}{2}\]
Um die Lösungen der quadratischen Ungleichungen \(-\frac{3}{8}x^{2} + 3x -\frac{9}{2} < 0\) und \(-\frac{3}{8}x^{2} + 3x -\frac{9}{2} > 0\) bestimmen zu können, wird der Funktionsterm \(f'(x)\) faktorisiert. Hierfür berechnet man beispielsweise mithilfe der Lösungsformel für quadratische Gleichungen die Nullstellen von \(f'\) und beschreibt damit den Funktionsterm \(f'(x)\) als Produkt seiner Linearfaktoren (vgl. 1. Lösungsansatz).
\[\begin{align*}f'(x) &= -\frac{3}{8}x^{2} + 3x - \frac{9}{2} \\[0.8em] &= -\frac{3}{8} \cdot (x^{2} - 8x + 12) & &| \; \text{Nullstellen:}\; x = 2; \; x = 6 \\[0.8em] &= -\frac{3}{8} \cdot (x - 2)(x - 6) \end{align*}\]
Mithilfe des faktorisierten Funktionsterms von \(f'(x)\) lassen sich die quadratischen Ungleichungen durch Fallunterscheidung lösen.
Untersuchung der Gültigkeit der Ungleichung \(f'(x) < 0\):
\[f'(x) = -\frac{3}{8} \cdot (x - 2)(x - 6)\]
\(f'(x) < 0\), falls \((x - 2)(x - 6) > 0\)
\((x - 2)(x - 6) > 0\), falls:
1. Fall
\[\begin{align*} x - 2 &< 0 &\wedge & & x - 6 &< 0 \\[0.8em] x &< 2 &\wedge & & x &< 6 \end{align*}\]
\(\Longrightarrow \quad x < 2\) bzw. \(x \in \; ]-\infty;2[\)
\(\Longrightarrow \quad f\) für \(x \in \; ]-\infty;2[\) streng monoton fallend
2. Fall
\[\begin{align*} x - 2 &> 0 &\wedge & & x - 6 &> 0 \\[0.8em] x &> 2 &\wedge & & x &> 6 \end{align*}\]
\(\Longrightarrow \quad x > 6\) bzw. \(x \in \; ]6;+\infty[\)
\(\Longrightarrow \quad f\) für \(x \in \; ]6;+\infty[\) streng monoton fallend
Untersuchung der Gültigkeit der Ungleichung \(f'(x) > 0\):
\[f'(x) = -\frac{3}{8} \cdot (x - 2)(x - 6)\]
\(f'(x) > 0\), falls \((x - 2)(x - 6) < 0\)
\((x - 2)(x - 6) < 0\), falls:
1. Fall
\[\begin{align*} x - 2 &< 0 &\wedge & & x - 6 &> 0 \\[0.8em] x &< 2 &\wedge & & x &> 6 \end{align*}\]
\(\Longrightarrow \quad\) keine Lösung
2. Fall
\[\begin{align*} x - 2 &> 0 &\wedge & & x - 6 &< 0 \\[0.8em] x &> 2 &\wedge & & x &< 6 \end{align*}\]
\(\Longrightarrow \quad 2 < x < 6\) bzw. \(x \in \; ]2;6[\)
\(\Longrightarrow \quad f\) für \(x \in \; ]2;6[\) streng monoton steigend
Alternative graphische Lösung der Ungleichungen \(f'(x) < 0\) und \(f'(x) > 0\):
\[f'(x) = -\frac{3}{8}x^{2} + 3x -\frac{9}{2}\]
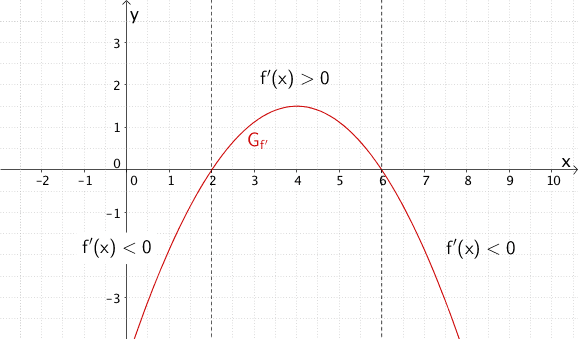
Der Graph der quadratischen Ableitungsfunktion \(f'\) ist eine nach unten geöffnete Parabel. An den einfachen Nullstellen \(x = 2\) und \(x = 6\) wechselt \(f'(x)\) das Vorzeichen. Das Monotonieverhalten von \(f\) kann dem Verlauf des Graphen von \(f'\) entnommen werden:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(f'(x) < 0\) für \(x < 2 \quad \Longrightarrow \quad f\) ist im Intervall \(]-\infty;2[\) streng monoton fallend.
\(f'(x) > 0\) für \(2 < x < 6 \quad \Longrightarrow \quad f\) ist im Intervall \(]2;6[\) streng monoton steigend.
\(f'(x) < 0\) für \(x > 6 \quad \Longrightarrow \quad f\) ist im Intervall \(]6;+\infty[\) streng monoton fallend.
Extrempunkte von \(G_{f}\):
In Kenntnis der Nullstellen \(x = 2\) und \(x = 6\) von \(f'\) und dem Vorzeichenwechsel von \(f'(x)\) lässt sich die Art der Extrempunkte schlussfolgern.
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[\left. \begin{align*} &f'(x) < 0 \; \text{für} \; x < 2 \\[0.8em] &f'(2) = 0 \\[0.8em] &f'(x) > 0 \; \text{für} \; 2 < x < 6 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\; TiP(2|f(2))\]
\[\left. \begin{align*} &f'(x) > 0 \; \text{für} \; 2 < x < 6 \\[0.8em] &f'(6) = 0 \\[0.8em] &f'(x) < 0 \; \text{für} \; x > 6 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}\; HoP(6|f(6))\]
Lage (\(y\)-Koordinate) der Extrempunkte:
\[\begin{align*} f(2) &= -\frac{1}{8} \cdot 2^{3} + \frac{3}{2} \cdot 2^{2} - \frac{9}{2} \cdot 2 \\[0.8em] &= -1 + 6 - 9 \\[0.8em] &= -4\end{align*}\]
\[\Longrightarrow \quad TiP(2|-4)\]
\[\begin{align*} f(6) &= -\frac{1}{8} \cdot 6^{3} + \frac{3}{2} \cdot 6^{2} - \frac{9}{2} \cdot 6 \\[0.8em] &= -27 + 54 + 27 \\[0.8em] &= 0\end{align*}\]
\[\Longrightarrow \quad HoP(6|0)\]

