Die Ebene \(N_k\) enthält die \(x_3\)-Achse und den Punkt \(P_k(1-k|k|0)\) mit \(k \in \; ]0;1[\). Welche Kanten des Körpers von \(N_k\) geschnitten werden, ist abhängig von \(k\). Durchläuft \(k\) alle Werte zwischen \(0\) und \(1\), so gibt es Bereiche \(]a;b[\), für die jeweils gilt, dass \(N_k\) für alle Werte von \(k \in \; ]a;b[\) die gleichen Kanten des Körpers schneidet. Bestimmen Sie den größten dieser Bereiche und geben Sie die zugehörigen Kanten an.
(4 BE)
Lösung zu Teilaufgabe e
Lage der Ebenen \(\boldsymbol{N_k}\)
Nachfolgende Überlegungen sind Voraussetzung für einen geeigneten Lösungsansatz. Sie müssen aber nicht dokumentiert werden.
Alle Ebenen \(N_k\) enthalten die \(x_3\)-Achse, d. h. die Ebenen rotieren um die \(x_3\)-Achse (Ebenenbüschl). Die Lage einer Ebene hängt von den Koordinaten des Punktes \(P(1-k|k|0)\) mit \(k \in\; ]0;1[\) ab.
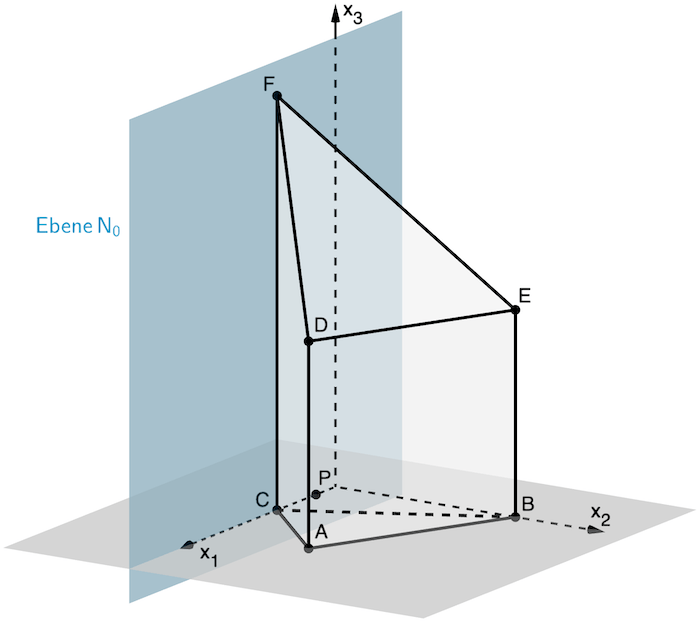
Für den nicht definierten Grenzfall \(k = 0\) enthält die Ebene \(N_0\) den Punkt \(P(1|0|0)\) und ist somit die \(x_1x_3\)-Ebene.
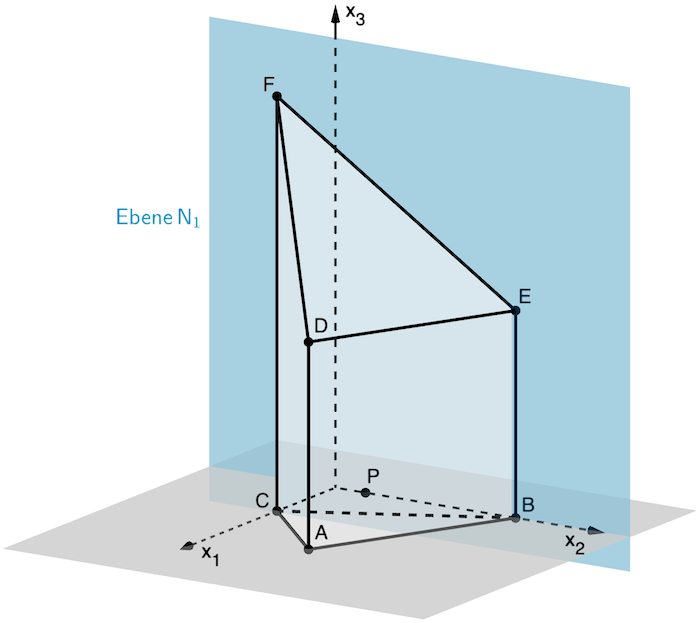
Für den nicht definierten Grenzfall \(k = 1\) enthält die Ebene \(N_1\) den Punkt \(P(0|1|0)\) und ist somit die \(x_2x_3\)-Ebene.
![Für k = 0,2 schneidet die Ebene N₀,₂ die Kanten [AC], [BC], [DF] und [EF]](/images/stories/B2023_PT_B_G2/B2023_PT_B_G2_e4.png)
Rotiert die Ebene \(N_k\) ausgehend von der \(x_1x_3\)-Ebene (Ebene \(N_0\)) gegen den Uhrzeigersinn, schneidet diese für alle Werte zwischen \(0\) und einem unbekannten Wert von \(k\) zunächst die Kanten \(\textcolor{#cc071e}{[AC]}\), \([\textcolor{#cc071e}{BC]}\), \(\textcolor{#cc071e}{[DF]}\) und \(\textcolor{#cc071e}{[EF]}\). Die Abbildung zeigt beispielhaft die Ebene \(\textcolor{#0087c1}{N_{0{,}2}}\) für \(k = 0{,}2\).
![Für einen bestimmten Wert von k enthält die Ebene Nk die Kante [AD]](/images/stories/B2023_PT_B_G2/B2023_PT_B_G2_e3.png)
Für einen bestimmten Wert von \(k\) enthält genau eine Ebene \(N_k\) die Punkte \(A\) und \(D\) (Kante \([AD]\)).
![Für k = 0,6 schneidet die Ebene N₀,₆ die Kanten [AB], [BC], [DE] und [EF]](/images/stories/B2023_PT_B_G2/B2023_PT_B_G2_e5.png)
Rotiert die Ebene \(N_k\) weiter gegen den Uhrzeigersinn, schneidet diese für alle Werte zwischen einem unbekannten Wert von \(k\) und \(1\) die Kanten \(\textcolor{#cc071e}{[AB]}\), \([\textcolor{#cc071e}{BC]}\), \(\textcolor{#cc071e}{[DE]}\) und \(\textcolor{#cc071e}{[EF]}\). Die Abbildung zeigt beispielhaft die Ebene \(\textcolor{#0087c1}{N_{0{,}6}}\) für \(k = 0{,}6\).
Derjenige Wert von \(k\), für den die Ebene \(N_{k_A}\) den Punkt \(A\) enthält, trennt die beiden Bereiche voneinander, für die die Ebenen \(N_k\) jeweils gleiche Kanten des Körpers schneiden.
1. Möglichkeit: Ebene \(\boldsymbol{N_{k_A}}\) betrachten, die den Punkt \(\boldsymbol{A}\) enthält
Vorgehensweise
- Gleichung von \(N_{k_A}\) mit \(A \in N_{k_A}\) ermitteln.
- Zugehörigen Wert von \(k\) mit \(P(1-k|k|0) \in N_{k_A}\) bestimmen.
- Bereiche \(k \in \; ]a;b[\) festlegen, für die die Ebenen \(N_k\) jeweils gleiche Kanten des Körpers schneiden.
- Für den größeren Bereich die zugehörigen Kanten angeben.
Gleichung der Ebene \(\boldsymbol{N_{k_A}}\) ermitteln
Der Vektor \(\begin{pmatrix} 0\\0\\1 \end{pmatrix}\) (\(N_k\) enthält die \(x_3\)-Achse) und der Ortsvektor \(\overrightarrow{A} = \begin{pmatrix} 6\\3\\0 \end{pmatrix}\) sind Richtungsvektoren dieser Ebene.
Das Vektorprodukt der beiden Richtungsvektoren erzeugt einen Normalenvektor der Ebene.
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*}\begin{pmatrix} 0\\0\\1 \end{pmatrix} \times \begin{pmatrix} 6\\3\\0 \end{pmatrix} &= \begin{pmatrix}0 & \cdot & 0 & - & 1 & \cdot & 3 \\ 1 & \cdot & 6 & - & 0 & \cdot & 0 \\ 0 & \cdot & 3 & - & 0 & \cdot & 6\end{pmatrix} \\[0.8em] &= \begin{pmatrix} -3 \\ 6 \\ 0 \end{pmatrix} = 3 \cdot \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix}\end{align*}\]
\(\overrightarrow{n} = \begin{pmatrix} -1 \\ 2 \\ 0 \end{pmatrix}\) ist ein Normalenvektor der Ebene \(N_{k_A}\)
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[\begin{align*} &N_{k_A} \colon n_1x_1 + n_2x_2 + n_3x_3 + n_0 = 0 \\[0.8em] &N_{k_A} \colon -x_1 + 2x_2 + n_0 = 0 &&| \; O(0|0|0) \in N_k \; \Rightarrow \; n_0 = 0 \\[0.8em] &N_{k_A} \colon -x_1 + 2x_2 = 0 \end{align*}\]
Zugehörigen Wert von \(\boldsymbol{k}\) bestimmen
Alle Ebenen \(N_k\) enthalten den Punkt \(P(1-k|k|0)\) (vgl. Angabe).
\[\begin{align*}P(\textcolor{#e9b509}{1-k}|\textcolor{#e9b509}{k}|0) \in N_{k_A} \colon -(\textcolor{#e9b509}{1-k}) + 2 \cdot \textcolor{#e9b509}{k} &= 0 \\[0.8em] -1 + 3k &= 0 &&| + 1 \\[0.8em] 3k &= 1 &&| :3 \\[0.8em] k &= \frac{1}{3}\end{align*}\]
Bereiche, für die die Ebenen \(\boldsymbol{N_k}\) jeweils gleiche Kanten des Körpers schneiden
Der Wert \(k = \dfrac{1}{3}\) trennt den Bereich \(k \in \; ]0;1[\) in die beiden Teilbereiche \(k \in\; ]0;\frac{1}{3}[\) und \(k \in \; ]\frac{1}{3};1[\) für die die Ebenen \(N_k\) jeweils gleiche Kanten des Körpers schneiden.
Beispiel für \(k \in \;]0;\frac{1}{3}[\): Ebene \(\textcolor{#0087c1}{N_{0{,}2}}\) für \(k = 0{,}2\)
Beispiel für \(k \in \;]\frac{1}{3};1[\): Ebene \(\textcolor{#0087c1}{N_{0{,}6}}\) für \(k = 0{,}6\)
Zugehörige Kanten für den größeren Bereich
Der Bereich \(k \in \;]\frac{1}{3};1[\) ist mit einer Intervalllänge von \(\frac{2}{3}\) der größere Bereich.
Für \(k \in \;]\frac{1}{3};1[\) schneiden die Ebenen \(N_k\) die Kanten \(\textcolor{#cc071e}{[AB]}\), \(\textcolor{#cc071e}{[BC]}\), \(\textcolor{#cc071e}{[DE]}\) und \(\textcolor{#cc071e}{[EF]}\) (Beispiel: Ebene \(\textcolor{#0087c1}{N_{0{,}6}}\) für \(k = 0{,}6\)).
2. Möglichkeit: Ursprungsgerade durch \(\boldsymbol{A}\) betrachten
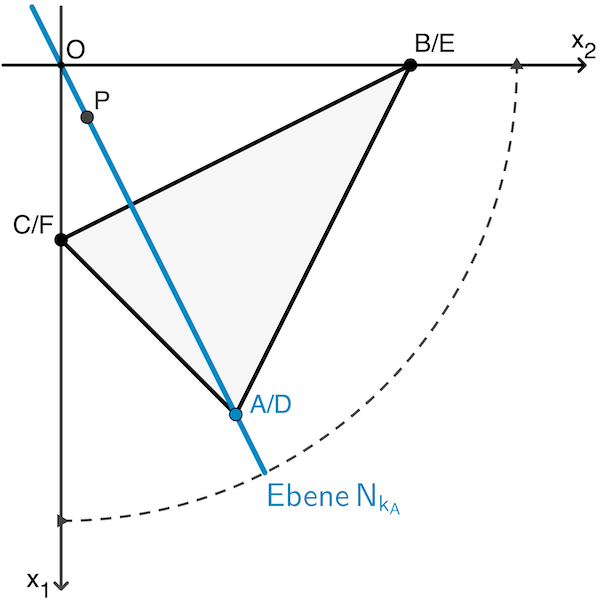
In der Aufsicht auf die \(x_1x_2\)-Ebene erscheint die Ebene \(\textcolor{#0087c1}{N_{k_A}}\) als Ursprungsgerade, welche durch den Punkt \(A\) verläuft.
Mithilfe der Gleichung dieser gedachten Ursprungsgerade lässt sich ebenfalls der Wert von \(k\) bestimmen, der die beiden Bereiche voneinander trennt, für die die Ebenen \(N_k\) jeweils gleiche Kanten des Körpers schneiden.
Gleichung der Ursprungsgerade \(\boldsymbol{OA}\) durch Punkt \(\boldsymbol{A}\)
\(O(0|0|0)\), \(A(6|3|0)\)
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[OA\colon \overrightarrow{X} = \overrightarrow{O} + \lambda \cdot \overrightarrow{A};\; \lambda \in \mathbb R\]
\[OA\colon \overrightarrow{X} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6\\3\\0 \end{pmatrix} = \lambda \cdot \begin{pmatrix} 6\\3\\0 \end{pmatrix}; \; \lambda \in \mathbb R\]
Zugehörigen Wert von \(\boldsymbol{k}\) bestimmen
Der Punkt \(\textcolor{#e9b509}{P(1-k|k|0)}\) liegt auf der Ursprungsgerade \(OA\).
\[P \in OA \colon \textcolor{#e9b509}{\begin{pmatrix}1-k\\k\\0 \end{pmatrix}} = \lambda \cdot \begin{pmatrix} 6\\3\\0 \end{pmatrix}\]
Koordinatenweise gelesen ergibt die Vektorgleichung ein lineares Gleichungssystem.
\[\begin{align*} \text{I} & & & 1 - k = 6 \lambda \\[0.8em] \text{II} & & \wedge \enspace & k = 3 \lambda \; \Leftrightarrow \; \lambda = \frac{k}{3} \\[0.8em] \text{III} & & \wedge \enspace & 0 = 0 \end{align*}\]
\(\lambda = \dfrac{k}{3}\) in Gleichung \(\text{I}\) eingesetzt:
\[\begin{align*} 1 - k &= 6 \cdot \frac{k}{3} \\[0.8em] 1 - k &= 2k &&| + k \\[0.8em] 1 &= 3k &&| : 3 \\[0.8em] k &= \frac{1}{3}\end{align*}\]
Weiter wie unter 1. Möglichkeit ausgeführt.
